 |
VI. Элементы физики атомного ядра
|
|
|
|
VI. Элементы физики атомного ядра
Заряд, масса и размеры атомных ядер. Зарядовое и массовое числа. Механический момент импульса ядра и его магнитный момент. Состав ядра. Нуклоны. Взаимодействие нуклонов, понятие о свойствах и природе ядерных сил. Дефект массы и энергия связи ядра. Радиоактивность. Закономерности и происхождение альфа-, бета- и гамма-излучения атомных ядер. Ядерные реакции и законы сохранения. Реакция деления атомных ядер. Капельная модель ядра. Цепная реакция деления. Критические размеры. Понятие о ядерной энергетике. Ядерные реакторы. Реакция синтеза атомных ядер. Проблема управляемых термоядерных реакций. Элементарные частицы. Их классификация и взаимная превращаемость. Кварки и глюоны.
VII. Современная физическая картина мира
Иерархия структур материи. Четыре типа фундаментальных взаимодействий: сильные, электромагнитные, слабые и гравитационные. Физический вакуум. Происхождение, эволюция и будущее Вселенной. Теория большого взрыва. Незавершенность современной физики. Основные этапы эволюции физики и становление новых форм рационального мышления.
ЭЛЕКТРОМАГНЕТИЗМ, ЭЛЕКТРОМАГНИТНЫЕ
КОЛЕБАНИЯ И ВОЛНЫ
ОСНОВНЫЕ ФОРМУЛЫ
| Магнитная индукция |
| |||||
| в вакууме (закон Био-Савара – Лапласа), где | ||||||
|
| ||||||
| Принцип суперпозиции для магнитного поля | 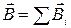
| |||||
| Поле прововодника произвольной формы с током I | 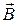 = = 
| |||||
| Магнитная индукция поля, создаваемого отрезком прямолинейного проводника, где b – расстояние от точки наблюдения до проводника a1 и a2 углы между векторами
| 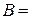 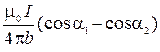
| |||||
| Магнитная индукция поля бесконечно длинного прямолинейного проводника (a1 = 0, a2 = p) | B = m0 I / 2p b | |||||
| Магнитная индукция поля на оси кругового тока, где R – радиус кривизны проводника, z – расстояние от центра витка до точки наблюдения. | 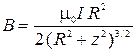
| |||||
| Магнитная индукция поля в центре кругового тока (z = 0) | B = m0 I / 2 R. | |||||
| Магнитная индукция поля на оси соленоида длиной l и радиусом R с числом витков N, где n = N / l – число витков на единицу длины, a1 и a2 углы между осью соленоида и радиусами-векторами, проведенными из точки наблюдения к краям соленоида | 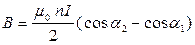
| |||||
|
Магнитная индукция поля - внутри длинного (l > > R, a1=p, a2=0) соленоида, | 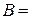 m0 n I m0 n I
| |||||
| - в центре основания длинного соленоида (l > > R, a1 =p/2, a2 = 0) | 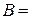 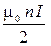
| |||||
| Циркуляция вектора магнитной индукции вдоль замкнутого контура | 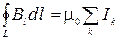
| |||||
| Сила, действующая на заряд q, движущийся со скоростью | 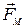 = q [ = q [ 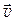 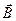 ], ], 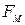 = qvB sin a = qvB sin a
| |||||
| сила, действующая на элемент проводника d | 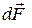 = I [ = I [ 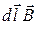 ] ]
| |||||
| Сила, действующая на прямолинейный проводник длиной L в однородном поле, где a - угол между направлением тока и вектором | 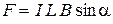
| |||||
| Магнитный поток через поверхность площадью dS, где a – угол между вектором нормали | dФ = B dS cos a = Bn dS | |||||
| Магнитный поток через поверхность S | Ф = 
| |||||
| Работа, совершаемая силой Ампера при перемещении в постоянном магнитном поле проводника длиной l с постоянным током I, где Ф – магнитный поток сквозь поверхность, образованную движением проводника | А = IФ | |||||
| Работа по перемещению замкнутого контура с постоянным током I в постоянном магнитном поле, где DФ – изменение магнитного потока сквозь поверхность, ограниченную контуром
| А = I DФ | |||||
| Магнитный момент контура с током I, где | 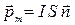
| |||||
|
Момент сил - в магнитном поле | 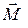 = [ = [ 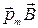 ] ]
| |||||
| - в неоднородном магнитном поле | 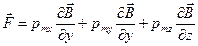
| |||||
| Сила, действующая на контур с током в в магнитном поле, изменяющемся только вдоль оси x, где a – угол между векторами | 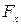 = = 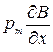 cos a cos a
| |||||
| Работа магнитного поля по перемещению проводника, по которому идёт ток I, где | 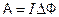
| |||||
| Основной закон электромагнитной индукции (закон Фарадея-Максвелла), где Ei – электродвижущая сила индукции; N – число витков в контуре; | 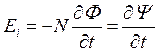
| |||||
| Разность потенциалов U на концах проводника длиной I, движущегося со скоростью υ в однородном магнитном поле, где α – угол между направлениями векторов скорости | 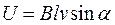
| |||||
| Электродвижущая сила индукции Еi, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью ω в однородном магнитном поле с индукцией | 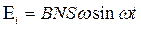
| |||||
| Количество электричества Q, протекающего в контуре, равно, где R – сопротивление контура; | 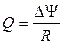
| |||||
| Электродвижущая сила самоиндукции Еi, возникающая в замкнутом контуре при изменении силы тока в нем, равна, где L – индуктивность контура | 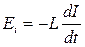
| |||||
| Потокосцепление контура, где L – индуктивность контура | 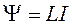
| |||||
|
Индуктивность соленоида (тороида) | 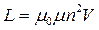
| |||||
| Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, где I – сила тока в контуре | 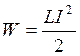
| |||||
| Объёмная (пространственная) плотность энергии однородного магнитного поля | 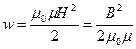
| |||||
| Намагниченность – магнитный момент единицы объема магнетика, где DV – физически бесконечно малый объем в окрестности данной точки,
| 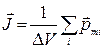
| |||||
|
Напряженность магнитного поля | 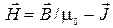
| |||||
| - в изотропной среде где | 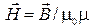 , ,
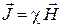 , ,
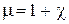 . .
| |||||
| Циркуляция вектора напряженности магнитного поля вдоль замкнутого контура пропорциональна алгебраической сумме макроскопических токов, охваченных этим контуром | 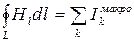
| |||||
| Условия на границе раздела двух сред с магнитными проницаемостями μ 1 и μ 2 при отсутствии макротоков, текущих по поверхности раздела сред, где
|  , , 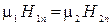 , ,
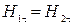 , , 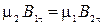 , ,
| |||||
|
Частота собственных незатухающих колебаний в контуре, где L – индуктивность контура; С – его электроёмкость. Период собственных незатухающих колебаний в контуре (Формула Томсона), | 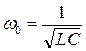 , ,
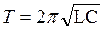
| |||||
| Затухающие колебания заряда конденсатора в контуре, где - частота затухающих колебаний, |  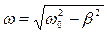
| |||||
| - коэффициент затухания, | 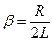
| |||||
| - логарифмический декремент затухания θ и добротность Q контура, | 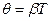 , , 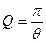 , , 
| |||||
| - при слабом затухании | 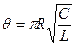 , , 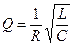
| |||||
Максимум амплитуды вынужденных колебаний заряда достигается при частоте 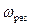
|
| |||||
| Связь длины электромагнитной волныс периодом Т и частотой ν колебаний, где с – скорость электромагнитных волн в вакууме (с=3· 108 м/с). |
| |||||
| Фазовая скоростьэлектромагнитных волн - в среде где ε – диэлектрическая проницаемость среды; μ – магнитная проницаемость среды, в которой распространяется волна, |
| |||||
| В бегущей электромагнитной волне |
| |||||
| Объёмная плотностьэнергии электромагнитного поля |
| |||||
| В неферромагнитной среде |
| |||||
| Плотность потока электромагнитной энергии (вектор Пойтинга) |
| |||||
| Интенсивность волны |
| |||||
| - для плоской монохроматической волны |
| |||||
Плотность потока энергии излучения диполя в волновой зоне
где r – расстояние от диполя до точки наблюдения; θ – угол между радиус-вектором 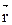 и осью диполя. и осью диполя.
|
| |||||
| Плотность потока импульса, переносимого электромагнитной волной |
| |||||
|
|
|



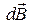 поля, создаваемого элементом проводника d
поля, создаваемого элементом проводника d 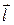 с постоянным током I
с постоянным током I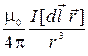
 – радиус-вектор, проведенный от элемента проводника в точку наблюдения, m0 = 4p 10 -7, Гн/м – магнитная постоянная.
– радиус-вектор, проведенный от элемента проводника в точку наблюдения, m0 = 4p 10 -7, Гн/м – магнитная постоянная.  и
и 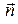 к поверхности dS, Bn – проекция вектора
к поверхности dS, Bn – проекция вектора 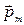 и
и  - изменение магнитного потока через поверхность, ограниченную контуром, по которому идет ток; I – сила тока в контуре
- изменение магнитного потока через поверхность, ограниченную контуром, по которому идет ток; I – сила тока в контуре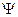 – потокосцепление
– потокосцепление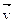 и магнитной индукции
и магнитной индукции 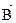
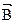 , где ω t – мгновенное значение угла между вектором
, где ω t – мгновенное значение угла между вектором 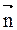 к плоскости рамки
к плоскости рамки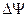 – изменение потокосцепления через контур
– изменение потокосцепления через контур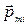 – магнитный момент i-го атома (молекулы).
– магнитный момент i-го атома (молекулы). 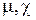 – соответственно магнитная проницаемость и магнитная восприимчивость вещества.
– соответственно магнитная проницаемость и магнитная восприимчивость вещества. 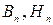 и
и 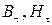 – нормальные и тангенциальные составляющие векторов
– нормальные и тангенциальные составляющие векторов 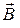 и
и 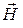 соответственно
соответственно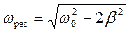
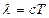 или
или 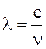
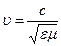 ,
, 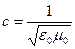
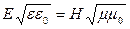
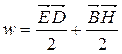
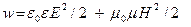
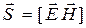
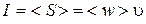
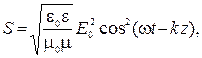
 .
. 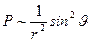 ,
, 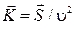 .
.