 |
Примеры решения задач. Решение. Поле витка, находящегося на расстоянии Х от центра катушки
|
|
|
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Однослойная катушка (соленоид) имеет длину l и радиус сечения R. Число витков на единицу длины n. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока I.
| l I R n |
Решение Поле витка, находящегося на расстоянии х от центра катушки |
|
| B -? |
где R – радиус сечения, μ 0 = 4p × 10-7 Гн/м – магнитная постоянная.
Тогда поле элемента dx длины соленоида
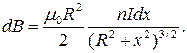 (2)
(2)
Поле в соленоиде
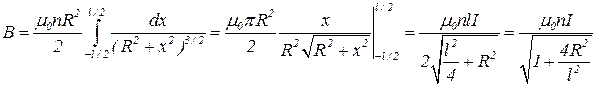 (3)
(3)
Проверка (3) на размерность: 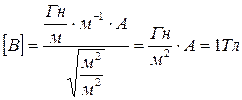
Ответ: индукция магнитного поля в центре катушки 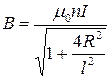 .
.
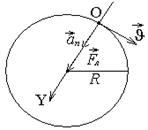
2. Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией B = 0, 015 Тл по окружности радиусом R = 10 см. Определить импульс р иона.
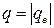 B = 0, 015 Тл
R = 10× 10-2 м
B = 0, 015 Тл
R = 10× 10-2 м
|
Решение Ион движется по окружности под действием магнитной составляющей силы Лоренца. По II-му закону Ньютона В проекции на нормаль |
|
| р -? |
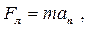 (1)
(1)
где аn – нормальное ускорение
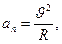 (2)
(2)
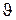 - скорость иона, R – радиус окружности.
- скорость иона, R – радиус окружности.
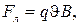 (3)
(3)
где q – заряд иона, 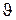 - его скорость, B – индукция магнитного поля.
- его скорость, B – индукция магнитного поля.
Подставляя (2), (3) в (1), получим
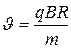 . (4)
. (4)
Импульс иона
р =  , (5)
, (5)
где m – масса иона.
Тогда, подставляя (5) в (6), получаем
|
|
|
 (6)
(6)
Проверка (6) на размерность:
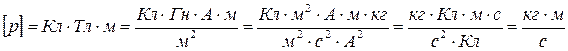 .
.
Вычисления:
р = 1, 6 × 10-19 × 0, 015 × 0, 1 = 2, 403 × 10-2 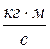 .
.
Ответ: импульс иона р =2, 403 × 10-2 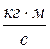 .
.
3. Постоянный ток I = 10 A течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины.
| I = 10 A |
Решение Cчитаем, что ток распределен по сечению равномерно с плотностью
|
| Ф/l -? |
где I – ток в проводнике, R – радиус поперечного сечения проводника.
Согласно закону полного тока
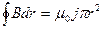 , (2)
, (2)
где 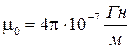 - магнитная постоянная, r – радиус замкнутого контура.
- магнитная постоянная, r – радиус замкнутого контура.
Из (1), (2) получим
2prB = 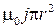
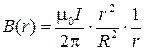 . (3)
. (3)
Поток через половину сечения на единицу длины
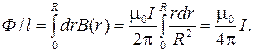 (4)
(4)
Проверка (4) на размерность:
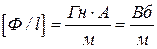 .
.
Вычисления:
Ф = 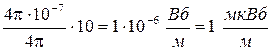 .
.
Ответ: магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины Ф = 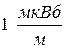 .
.
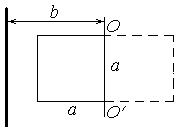
4. Квадратная проволочная рамка со стороной а и прямой проводник с постоянным током I лежат в одной плоскости (рис. ). Сопротивление рамки R, ее повернули на 180о вокруг оси, отстоящей от проводника с током на расстоянии b. Найти количество электричества, протекшее в рамке.
| I R a b |
Решение Индукция магнитного поля, создаваемого током прямолинейного проводника
|
|
| q -? |
где 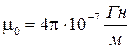 - магнитная постоянная, I – ток в проводнике, r – радиус поперечного сечения проводника.
- магнитная постоянная, I – ток в проводнике, r – радиус поперечного сечения проводника.
Пусть ток течет «вверх», а нормаль к рамке направлена за плоскость рисунка. Начальный поток через рамку
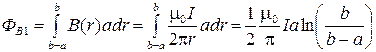 . (2)
. (2)
Конечный поток через рамку

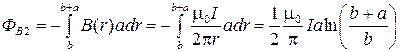 . (3)
. (3)
ЭДС индукции, возникающая в рамке при ее повороте
|
|
|
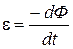 . (4)
. (4)
По закону Ома для участка цепи
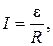 (5)
(5)
e - ЭДС индукции, R - сопротивление проводника.
Сила тока по определению
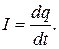 (6)
(6)
Подставляя (6) в (5) и получившийся результат в (4), имеем
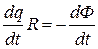 ,
,
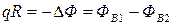 . (7)
. (7)
Подставляя (2), (3) в (7), окончательно получим
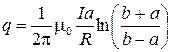 . (8)
. (8)
Проверка (8) на размерность:
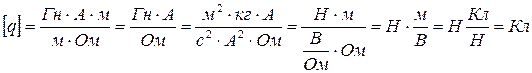
Ответ: количество электричества, протекшее в рамке, равно
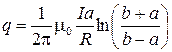 .
.
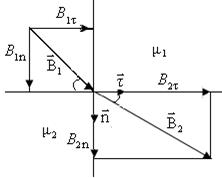
5. В среде с магнитной проницаемостью μ 1 векторы В 1 и Н 1 направлены под углом α 1 к границе раздела со средой, имеющей магнитную проницаемость μ 2. Определить величину и направление векторов В 2 и Н 2 во второй среде.
|
Решение | ||
| μ 1 |
| Согласно условиям для векторов В и Н на границе раздела магнетиков проекции этих векторов на направления
|
| В1 | ||
| Н1 | ||
| α 1 | ||
| В2 -? | ||
| Н2 -? | ||
| α 2 -? | ||
В соответствии с условием задачи и рисунком
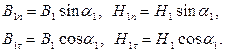 (2)
(2)
Из (1) и (2)
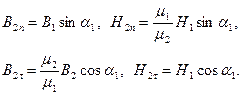 (3)
(3)
По проекциям 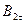 и
и 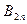 ,
, 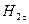 и
и 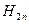 , находим модули векторов В 2 и Н 2:
, находим модули векторов В 2 и Н 2:
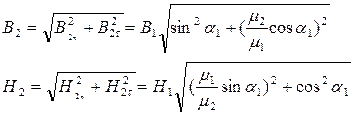 (4)
(4)
Направления векторов В 2 и Н 2 совпадают, так как оба магнетика однородные и изотропные. По (3) и рисунку
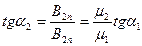 (5)
(5)
Размерности полученных величин совпадают с размерностями заданных в условии задачи.
Ответ: Величина магнитной индукции и напряжённости магнитного поля во втором магнетике составляют
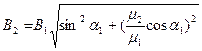 и
и 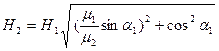 ,
,
вектор магнитной индукции во втором магнетике составляет с нормалью с границей раздела магнетиков угол 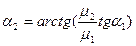 .
.
6. В колебательный контур включён источник ЭДС с амплитудой
e0 = 10 В. Амплитуда напряжения на конденсаторе при резонансе U0 = 200 В. Определить добротность Q контура.
|
Решение | ||||
| e0 = 10 В | Амплитуда напряжения U0 на конденсаторе связана с амплитудой тока I0 в последовательной цепи 1RLC2 переменного тока соотношением
|
| ||
| U0 = 200 В | ||||
| Q -? | ||||
При резонансе 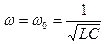 , а полное сопротивление Z цепи 1RLC2 равно её активному сопротивлению R, т. е.
, а полное сопротивление Z цепи 1RLC2 равно её активному сопротивлению R, т. е.
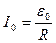 . (2)
. (2)
Подставив в (1)  и исключив из (1) и (2) I0, получим
и исключив из (1) и (2) I0, получим
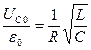 . (3)
. (3)
Так как 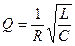 , то
, то 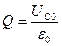 . Величина добротности, очевидно, является безразмерной.
. Величина добротности, очевидно, является безразмерной.
Вычисления:
Q= 20.
Ответ: добротность контура Q= 20.
7. В вакууме вдоль оси z распространяется плоская монохроматическая синусоидальная электромагнитная волна частоты ν = 50 МГц с амплитудой напряженности электрического поля Е0 = 100 мВ/м. Определить интенсивность волны, амплитуду напряженности магнитного поля и амплитудное значение тока смещения.
| Решение | |
| ν = 50 МГц | Амплитуды 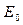 и и 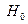 колебаний векторовнапряженностей колебаний векторовнапряженностей
|
| Е0 = 100 мВ/м | электрического Е и магнитного В полей в электромагнит- |
| I -? | ной волне связаны соотношением 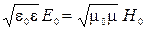 , где ε и , где ε и
|
| H0 -? | μ – диэлектрическая и маг нитная проницаемости среды, в |
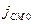 -? -?
| вакууме ε = 1, μ =1; ε 0 и μ 0 – электрическая и магнитная |
постоянные. Отсюда
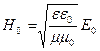 .
.
Интенсивность волны равна среднему значению вектора Пойнтинга
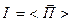 , т. е.
, т. е.  .
.
Напряженность электрического поля гармонической монохроматической плоской волны 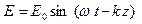 , где
, где 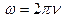 – циклическая частота волны. Вектор электрического смещения
– циклическая частота волны. Вектор электрического смещения 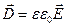 . Током смещения называется величина
. Током смещения называется величина 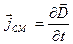 . Тогда
. Тогда 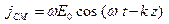 , и амплитудное значение тока смещения составит
, и амплитудное значение тока смещения составит 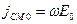 или
или  .
.
Проверка на размерность:
[Н0]= (( Ф/м)/(Гн/м))0, 5 · (В/м) = (( Кл/В)/(В·с/А))0, 5 · (В/м) =
= (( А2 · с /В)/(В2 · с))0, 5 · (В/м) = А/м.
[I] = ( А/м) · (В/м) Вт/м2.
[ 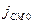 ] = (1/с) · ( Ф/м) · (В/м)= (1/с) · ( Кл/В) · (В/м2 ) = (1/с) · ( А·с/м2)= А·м2.
] = (1/с) · ( Ф/м) · (В/м)= (1/с) · ( Кл/В) · (В/м2 ) = (1/с) · ( А·с/м2)= А·м2.
Вычисления:
 ,
,
 ,
,
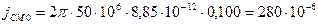 .
.
Ответ: Напряженность магнитного поля 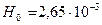 А/м, интенсивность волны
А/м, интенсивность волны 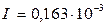 Вт/м2, амплитуда тока смещения
Вт/м2, амплитуда тока смещения 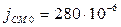 А.
А.
|
|
|



 (1)
(1)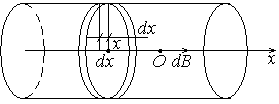
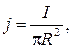 (1)
(1)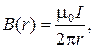 (1)
(1)
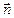 и
и 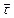 связаны соотношениями
связаны соотношениями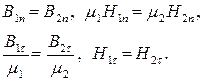 (1)
(1)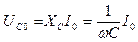 . (1)
. (1)