Главная | Обратная связь | Поможем написать вашу работу!

Задачи по теме «Основы электродинамики»

201. Частица совершает колебания по закону x =30 10^-2 cos(1, 5 t), м. Определить ускорение частицы в момент времени, когда ее скорость равна v = 8, 0 10^-2 м/с.

202. Частица совершает колебания по закону x =3, 0 10^-2 cos(2, 5 t), м. Определить скорость частицы в момент времени, когда ее ускорение равна а= 5, 0 10^-2 м/с².

203. Частица совершает гармонические колебания с частотой n = 4, 5 Гц и амплитудой А = 3, 0 10^-2 м. Каковы скорость и ускорение частицы, когда ее смещение равно х = 6, 0 10^-2 м?

204. Частица совершает колебания по закону x =4, 0 10^-2 sin (5, 5 t + 50^о), м. Каковы максимальная скорость и ускорение частицы?

205. Частица совершает гармонические колебания. Наибольшее смещение частицы А = 2, 0 10^-2 м, наибольшая скорость v_m = 8, 5 10^-2 м/с. Найти период колебаний.

206. Частица совершает колебания по закону x = A cos w t. В некоторый момент смещение х₁ = 3, 5 10^-2 м. Когда фаза колебаний увеличилась вдвое, смещение частицы равно х₂ = 0, 4 10^-2 м. Найти амплитуду колебаний.

207. Частица совершает гармонические колебания. Максимальная скорость частицы v_m=0, 40 10^-2 м/с, максимальное ускорение а_m = 40 10^-2 м/с². Найти период колебаний.

208. Два одинаково направленных гармонических колебания одного периода с амплитудами A₁ = 2, 0 10^-2 м и A₂= 1, 0 10^-2 м складываются в одно колебание с амплитудой А = 2, 0 10^-2 м. Найти разность фаз складываемых колебаний.

209. Частица совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x =3, 0 10^-2 sin w t и y =4, 0 10^-2 sin (w t + 45^о). Найти уравнение траектории частицы, построить ее и указать направление движения.

210. Два математических маятника, один длиной l =0, 6 м, другой 1, 7l совершают колебания с одинаковыми угловыми амплитудами. Определить периоды колебаний и отношение их энергий, если масса шарика второго маятника в k = 3, 5 раз больше массы первого.

211. Частица массой m = 30 10^-3 кг совершает колебания по закону x =7, 0 10^-2 sin 3, 5 t, м. Определить максимальное значение возвращающей силы и кинетической энергии.

212. Частица массой m = 30 10^-3 кг совершает колебания по закону x =5, 0 10^-2 sin 4, 5 t, м. Определить значение возвращающей силы в момент t = 3, 0 с и полную энергию частицы.

213. Груз, подвешенный к пружине, колеблется по вертикали с амплитудой А = 3, 0 10^-2 м. Определить полную энергию колебаний, если жесткость пружины равна k = 1, 5 кН/м.

214. Физический маятник в виде тонкого прямого стержня длиной l =1, 6 м колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на расстоянии а = 0, 3 м от верхнего конца стержня. Найти период колебаний маятника.

215. Диск радиусом R = 0, 25 м колеблется около горизонтальной оси, проходящей перпендикулярно плоскости диска через точку, удаленную на расстоянии а = 0, 10 м от центра диска. Найти период колебаний маятника.

216. На конце стержня длиной l = 1, 4 м укреплен груз, масса которого намного больше массы стержня. Стержень с грузом колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на расстоянии а = 0, 4 м от верхнего конца стержня. Найти период колебаний маятника.

217. Полная энергия тела, совершающего гармонические колебания, равна Е = 7, 0 10^-7 Дж, амплитуда колебаний А = 2, 0 10^-2 м. Определить смещение, при котором на тело действует сила F = 4, 0 10^-5 Н, и максимальное значение возвращающей силы.

218. Железный шарик массой m = 45 10^-3 кг, подвешенный на нити длиной l = 1, 3 м, совершает гармонические колебания. Если снизу под шарик поместить магнит, то он будет притягивать шарик с постоянной силой F= 0, 30 Н. Определить частоту колебаний маятника в новом состоянии.

219. Найти потенциальную энергию математического маятника массой m = 40 10^-3 кг при угле отклонения нити a = 4, 0 град, если период колебаний равен Т= 1, 40 с.

220. Математический маятник длиной l = 1, 6 м подвешен в вагоне, движущемся горизонтально с ускорением а = 2, 0 м/с². Определить период колебаний маятника.

221. На нити в воздухе подвешен шарик массой m = 0, 53 кг зарядом q = 2, 4 10^-6 Кл. Какой заряд надо поднести к нему снизу на расстоянии r = 29 10^-2 м, чтобы период колебаний уменьшился в 2 раза?

222. Сила кулоновского отталкивания двух частиц массами m₁ = 4, 3 10^-2 кг и m₂ =2, 4 10^-2 кг уравновешивается силой гравитационного притяжения. Заряд первой частицы q₁ = 5, 1 10^-13 Кл. Каков заряд второй частицы?

223. Заряды q₁= -5, 0 10^-6 Кл и q₂ = 40 10^-6 Кл находятся на расстоянии r = 55 10^-2 м друг от друга. Определить положение точки на прямой, соединяющей эти заряды, в которое нужно поместить заряд q₀ так, чтобы система находилась в равновесии.

224. Два одинаковых шарика массой m = 2, 5 10^-3 кг каждый подвешены в одной точке на шелковых нитях длиной l = 0, 70 м. Какие заряды нужно сообщить шарикам, чтобы каждая нить составляла с вертикалью угол a = 45°?

225. Расстояние между двумя точечными зарядами q₁ = 5, 0 мкКл и q₂ = -4, 0 мкКл равно 10 см. Определить силу F, действующую на точечный заряд Q = 0, 1 мкКл, удалённый на r₁ = 6 см от первого и на r₂ = 8 см от второго зарядов.

226. Тонкий длинный стержень равномерно заряжен с линейной плотностью t = 6, 0 10^-8 Кл/м. На продолжении оси стержня на расстоянии a =0, 40 м от его конца находится точечный заряд q = 6, 6 10^-7 Кл. Определить силу взаимодействия стержня и заряда.

227. Заряд равномерно заряженного тонкого кольца радиуса R = 0, 10 м равен Q = 6, 0 10^-8 Кл. Найти силу, действующую на пылинку с зарядом q = 5, 0 нКл, находящуюся на расстоянии h = 0, 4 м от центра кольца по перпендикуляру, восставленному к плоскости в центре кольца

228. Заряды q₁=6, 6 10^-7 Кл и q₂ =4, 0 10^-7 Кл находятся на расстоянии l = 0, 60 м друг от друга. Найти потенциал поля зарядов в точке, расположенной между зарядами на соединяющей их линии на расстоянии r = 0, 1 м от первого заряда.

229. Расстояние между двумя точечными зарядами q₁ = 7Q и q₂ =- Q равно d = 5, 5 10^-2 м. На каком расстоянии r от первого заряда находится точка, в которой напряжённость Е поля зарядов равна нулю?

230. Тонкое полукольцо радиусом R = 5, 5 10^-2 м равномерно заряжено с линейной плотностью t = 4, 4 10^-8 Кл/м. Найти напряженность электрического поля в центре кривизны полукольца.

231. Поверхностная плотность заряда бесконечно протяженной вертикальной плоскости равна s = 3, 0 10^-5 Кл/м². К плоскости на нити подвешен заряженный шарик массой m = 20 10^-3 кг. Определить заряд шарика, если нить образует с плоскостью угол a = 30 град.

232. Определить напряжённость электрического поля между двумя бесконечными параллельными пластинами, равномерно заряженными с поверхностными плотностями s₁= 3, 0 10^-6 Кл/м² и s₂= 6, 5 10^-6 Кл/м².

233. Напряжённость электрического поля в точке, отстоящей на расстоянии a = 0, 8 мот осевой линии бесконечного цилиндра радиусом r = 0, 4 м, равна Е = 1, 5 кВ/м. Определить поверхностную плотность заряда s.

234. Две концентрические сферы, радиусы которых R₁ = 7, 0 см и R₂ = 30 см, заряжены равномерно. На внутренней сфере находится заряд q₁ = 3, 0 10^–7 Кл, а на внешней q₂= -2, 0 10^–7 Кл. Определить напряжённость электрического поля в точках, находящихся соответственно на расстоянии 1, 5, 10 и 20 см от общего центра обеих сфер.

235. Заряженная капля жидкости массой m =0, 24 10^-3 кг находится в равновесии в поле горизонтально расположенного плоского конденсатора. Расстояние между пластинами конденсатора d = 3, 3 10^-3 м, разность потенциалов между ними Dj =150 В. Определить заряд капли.

236. Заряд равномерно заряженной сферической поверхности радиуса R=30 10^-2 м равен Q = 6, 5 10^-6 Кл. Определить напряжённость и потенциал электрического поля внутри и снаружи поверхности.

237. Цилиндрический конденсатор, радиусы внутреннего и внешнего цилиндров которого равны R₁ = 3, 0 см и R₂ = 7, 0 см, заряжен до разности потенциалов j₁ - j₂ = 140 В. Какова напряжённость электрического поля на середине расстояния между цилиндрами?

238. Две параллельные, бесконечно длинные нити, равномерно заряженные с линейными плотностями t₁ = 1, 0 10^-7 Кл/м и t₂ = 1, 2 10^-7 Кл/м находятся на расстоянии d = 15 см. Определить силу взаимодействия, приходящуюся на отрезок нити длиной 1 cм.

239. Две одинаковые круглые пластины площадью по S = 100 см² каждая расположены параллельно друг другу. Заряд одной Q₁ = 1, 0 10^-7 Кл, другой Q₂= 1, 2 10^-7 Кл. Определить силу взаимодействия пластин, если расстояние между ними равно d = 0, 15 см.

240. Тонкое кольцо радиусом R = 0, 10 м равномерно заряжено с линейной плотностью t = 6, 0 10^-8 Кл/м. Определить потенциал в точке, находящейся на оси кольца на расстоянии h = 0, 40 см от центра

241. На расстоянии d = 5, 0 см от бесконечной проводящей толстой пластины находится точечный заряд q = 1, 0 нКл. Определить напряженность электрического поля у поверхности пластины.

242. Найти потенциал незаряженного проводящего шара, на расстоянии r = 100 см от центра которого расположен точечный заряд q = 0, 8 нКл.

243. Бесконечно длинная тонкая прямая нить равномерно заряжена с линейной плотностью t = 6, 0 10^-8 Кл/м. Определить разность потенциалов двух точек поля, удаленных от нити на r₁= 1, 5 см и r₂ = 4, 0 м.

244. Определить потенциал, до которого можно зарядить уединенный металлический шар радиусом R = 3, 5 мв диэлектрической среде, если напряженность электрического поля, при котором происходит пробой среды Е_пр. = 0, 8 МВ/м

245. Плоский конденсатор содержит два слоя диэлектриков с диэлектрической проницаемостью и толщиной e₁ = 5, 0, d₁= 1, 6 мм и e₂= 3, 0, d₂. = 1, 4 мм. Найти напряжённость электрического поля в каждом слое, если к обкладкам конденсатора приложена разность потенциалов U = 200 В.

246. Две параллельные пластины заряжены с поверхностной плотностью s₁ = 3, 0 мкКл/м² и s₂. = 1, 4 мкКл/м². Расстояние между ними d = 16 мм. Между пластинами вплотную к ним вставлена пластина диэлектрика с диэлектрической проницаемостью e = 5, 0. Определить разность потенциалов между пластинами.

247. Плоский слой диэлектрика с диэлектрической проницаемостью e = 5, 0 толщиной d = 16 мм равномерно заряжен с объемной плотностью r = 3, 0 нКл/м³. Определить напряжённость электрического поля внутри слоя на расстоянии l = 1, 4 мм от поверхности.

248. N = 70 одинаковых капель ртути, заряженных до потенциала j = 30 В, сливаются в одну. Каков потенциал образовавшейся капли?

249. Два одинаковых металлических шарика радиусом r = 1, 6 мм расположены в среде с диэлектрической проницаемостью e = 2, 8 так, что расстояние между их центрами равно d = 35 см. Найти емкость такой системы.

250. Два параллельных цилиндрических провода радиусом r = 0, 60 мм расположены в среде с диэлектрической проницаемостью e = 2, 4 так, что расстояние между их осями равно d = 15 см. Найти емкость единицы длины такой системы.

251. Определить ёмкость плоского конденсатора с двумя слоями диэлектриков с диэлектрической проницаемостью и толщиной e₁ = 5, 0, d₁ = 1, 6 мм и e₂ = 3, 0, d₂ = 1, 4 мм. Площадь пластин S = 50 см².

252. Определить ёмкость цилиндрического конденсатора с диэлектриком с диэлектрической проницаемостью e = 5, 0. Высота конденсатора h = 13 см, радиусы обкладок r₁ = 3, 0 см и r₂ = 2, 4 см.

253. Определить ёмкость сферического конденсатора с диэлектриком с диэлектрической проницаемостью e = 3, 0, радиусы обкладок r₁= 6, 0 см и r₂ =5, 7 см.

254. Заряд сферического конденсатора равен Q = 3, 0 мкКл. Радиусы обкладок R₁=3, 0 см, R₂ = 2, 4 см. Промежуток между ними заполнен диэлектриком с диэлектрической проницаемостью e = 2, 0. Определить разность потенциалов между обкладками.

255. Металлический шар радиусом R = 20 мм, имеющий заряд q = 2, 0 мкКл, окружён слоем диэлектрика толщиной d = 5, 5 мм с диэлектрической проницаемостью e= 2, 5. Определить энергию электрического поля, сосредоточенного в слое диэлектрика.

256. На уединённом проводящем шаре радиусом R = 2, 0 см находится заряд Q = 30 мкКл. Какую работу надо совершить, чтобы добавить к заряду на шаре заряд q = 2, 0 мкКл, находящийся первоначально на расстоянии, очень большом по сравнению с радиусом шара?

257. Заряды двух конденсаторов ёмкостью С₁ = 2, 5 мкФ и С₂ = 3, 0 мкФ соответственно равны q₁ = 500 мкКл и q₂ = 150 мкКл. Найти изменение энергии при параллельном соединении этих конденсаторов.

258. Обкладки плоского воздушного конденсатора площадью S = 300 см² каждая, расположены на расстоянии d₁=1, 6 мм друг от друга. Какую работу надо совершить, чтобы увеличить расстояние между обкладками до d₂ = 2, 4 мм при условии, что конденсатор заряжают до разности потенциалов U = 150 В и отключают от батареи?

259. Обкладки плоского воздушного конденсатора площадью S = 350 см² каждая, расположены на расстоянии d₁ = 1, 7 мм друг от друга. Какую работу надо совершить, чтобы увеличить расстояние между обкладками до d₂ = 2, 0 мм при условии, что конденсатор всё время соединён с батареей, ЭДС которой e = 100 В.

260. Плоский воздушный конденсатор с площадью обкладок S = 300 см² каждая и расстоянием между ними d = 5, 6 мм заряжается до разности потенциалов U = 150 В и отключается от батареи. Как изменятся ёмкость и энергия конденсатора, если в пространство между обкладками параллельно им ввести металлическую пластину такой же площади и толщины h = 1, 6 мм?

261. Два источника тока ( e₁ = 5, 0 В, r₁ = 1, 6 Ом; e₂ = 3, 0 В, r₂= 1, 4 Ом ) и резистор R = 25 Омсоединены, как показано на рис. 1. Найти силу тока в резисторе.

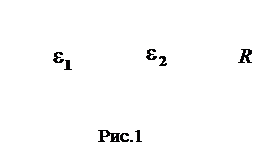
262. Два источника тока ( e₁ = 5, 0 В, r₁ = 1, 6 Ом; e₂ = 3, 0 В, r₂= 1, 4 Ом ) и одинаковые резисторы ( R = R₁ = 25 Ом ) соединены, как показано на рис. 2. Найти силу тока в резисторе R₁.

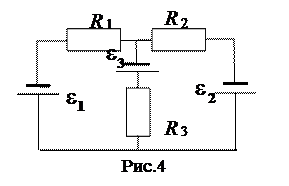263. Два источника тока ( e₁ = e₂ = e = 5, 0 В ) и резисторы ( R₁ = 350 Ом, R₂= 200 Ом ) соединены, как показано на рис. 3. Сопротивление вольтметра R_v = 200 Ом. Внутреннее сопротивление источников пренебрежимо мало. Что покажет вольтметр?

264. Источники тока ( e₁=5, 0 В, e₂=3, 0 В, e₃= 1, 0 В ) и резисторы ( R₁ = 16 Ом, R₂ = 1, 4 Ом, R₃ = 2, 5 Ом ) соединены, как показано на рис. 4. Внутреннее сопротивление источников пренебрежимо мало. Найти силу тока в источнике e₃ .

265. Два элемента ( e₁ = 4, 0 В, r₁ = 0, 16 Ом; e₂ = 6, 0 В, r₂ = 0, 14 Ом) соединены параллельно, а к местам соединения подключен вольтметр, сопротивление которого R = 25 Ом. Определить показание вольтметра.

266. В схеме, приведенной на рис. 5, ток через батарею с ЭДСe₁ = 3, 5 В не идет. Внутреннее сопротивление источников пренебрежимо мало. Определить силу тока в сопротивлении R₃ =6, 8 Ом и величину сопротивления R₁.

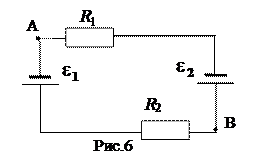
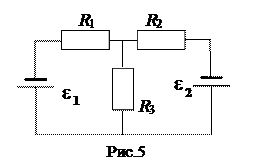
267. Найти разность потенциалов между точками А и В схемы (рис. 6). Внутреннее сопротивление источников пренебрежимо мало. (R₁ = 25 Ом, e₁ = 5, 0 В, R₂ = 14 Ом, e₂ = 3, 0 В).

268. По проводнику, сопротивление которого R = 4, 5 Ом, течет постоянный ток. За время t = 6, 3 с в проводнике выделилась теплота Q = 354 Дж. Определить заряд, протекший за это время по проводнику.

269. При выключении источника сила тока в цепи изменяется по закону

I =3, 5 e ^-⁴⁵⁰^t, А. Какой заряд протечет в цепи?

270. Сила тока в цепи изменяется по закону I =1, 2 sin w t. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 5, 0 Ом за время от t₁ = 0 до t₂ = Т/2, если Т = 1, 0 с.

271. Сила тока в цепи изменяется по закону I =2, 0 cos w t. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 4, 0 Ом за время от t₁ = 0 до t₂ = Т/4 с, если Т = 1, 0 с.

272. Сила тока в проводнике с сопротивлением R = 5, 0 Ом равномерно убывает от значения I₁= 3, 5 А до I₂= 1, 0 А в течение времени от t₁ = 0 до t₂ = 4, 0 с. Определить количество теплоты, которое выделится в проводнике.

273. Сила тока в цепи изменяется по закону I =1, 2 (1+ sin wt ), А. Какой заряд протечет в цепи за время от t₁ = 0 до t₂ = Т, если Т=1, 0 с?

274. При выключении источника сила тока в цепи изменяется по закону I =3, 5 e ^-⁴⁵⁰^t, А. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 5, 0 Ом после выключении источника.

275. Сила тока в проводнике с сопротивлением R = 5, 0 Ом равномерно возрастает от значения I₁= 1, 0 А до I₂= 3, 5 А в течение времени от t₁ = 0 до t₂ = 4, 0 с. Определить количество теплоты, которое выделится в проводнике

276. Сила тока в цепи изменяется по закону I =3, 5 ( 1 - e ^-^t^/^{3, 0}), А. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 5, 0 Ом в течение времени от t₁ = 0 до t₂ = 30 с.

277. Батарея состоит из пяти последовательно соединенных источников ЭДС с e = 3, 0 В и внутренним сопротивлением r = 0, 3 Ом каждого. Чему равна наибольшая мощность, которую можно получить от батареи?

278. Сила тока в цепи изменяется по закону I =3, 0 ( 1 - e ^-^t^/^{2, 0}). ). Какой заряд протечет в цепи за время от t₁ = 0 до t₂ = 20 с. ?

279. Во внешней цепи из двух одинаковых резисторов сопротивлением R = 2, 0 Ом каждого, выделяется одинаковая мощность как при параллельном, так и при последовательном их соединении. Найти мощность, выделяемую во внешней цепи, если ЭДС источника e = 15 В.

280. При подключении к источнику тока с ЭДС e = 24 В резистора с сопротивлением R = 30 Ом КПД источника составляет h 60 %. Какую максимальную мощность во внешней цепи может выделить данный источник?

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Воспользуйтесь поиском по сайту: