 |
Задачи, связянные с определением оптимальных потоков в сети
|
|
|
|
ЗАНЯТИЕ 5
СЕТЕВЫЕ ЗАДАЧИ
ЗАДАЧИ, СВЯЗЯННЫЕ С ОПРЕДЕЛЕНИЕМ КРАТЧАЙШЕГО И КРИТИЧЕСКОГО ПУТЕЙ
Словесная формулировка. Необходимо найти кратчайший или самый протяженный (критический) путь между заданными исходной и конечной вершинами (узлами, пунктами) сети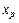 
и 
.
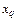Формальная постановка. Пусть задана сеть с графом 
и матрицей инцидентности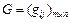 
; при этом каждой дуге 
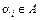сопоставлено число 
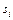, означающее длину этой дуги. Введем в рассмотрение переменные 
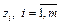, значения которых определяются следующим образом: 
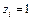, если дуга 
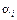присутствует в пути; 
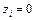в противном случае.
Тогда задача о кратчайшем (критическом) пути предстает в виде задачи линейного дискретного программирования:
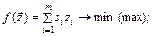(1.1.1)
(1.1.2)
Ограничения (1.1.2) являются необходимыми условиями, при которых набор дуг, соответствующих ненулевым значениям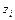 
, образует путь, соединяющи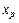й и .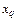
ЗАДАЧИ, СВЯЗЯННЫЕ С ОПРЕДЕЛЕНИЕМ ОПТИМАЛЬНЫХ ПОТОКОВ В СЕТИ
Задача о максимальном потоке. Словесная формулировка. Необходимо рассчитать величины потоков по дугам графа сети, которые бы обеспечивали максимальный приток в узел-приемник 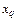. При этом величина данного притока должна быть равна величине истока из узла-источника 
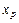, а величины потоков по всем дугам сети не должны превышать их пропускные способности, заданные числами. Суммарный приток по каждому узлу сети (за исключением приемника и источника) при этом должен быть равен суммарному истоку из этого узла (для исключения скоплений и дефицита потока).
Формальная постановка. Рассмотрим сеть с графом 
, матрица инцидентности 
которого задана. Предположим, что каждой дуге 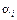сопоставлено число 
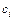, означающее «пропускную способность» этой дуги (у.е.). Обозначим через 
, величину потока по дуге 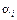. Тогда задача о максимальном потоке принимает вид
|
|
|
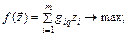(1.2.1)
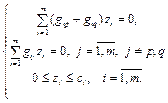(1.2.2)
Здесь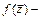 
суммарный втекающий в узел-приемник 
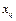поток. Первое ограничение в системе ограничений (1.2.2) означает равенство вытекающего из 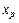и втекающего в 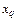потоков. Второе ограничение означает условие исключения скоплений и дефицита потока для любого промежуточного узла сети. Третье ограничение в (1.2.2) означает условие того, что потоки по дугам не могут превысить заданные предельно допустимые значения (пропускные способности дуг).
Задача о потоке минимальной стоимости. Словесная формулировка. Нужно рассчитать величины потоков минимальной суммарной стоимости по дугам сети, которые бы обеспечивали заданный суммарный приток в узел-приемник .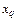
Формальная постановка. Пусть задана сеть с графом , и матрицей инцидентности . Предположим, что каждой дуге 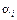сопоставлены числа 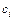и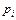 
, означающие «пропускную способность» этой дуги и стоимость единицы потока соответственно (у.е.). Пусть величина притока в узле-приемнике должна быть не меньше некоторой заданной величины 
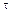. Обозначим через 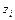величину потока по дуге 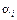. Тогда задача о потоке минимальной стоимости сводится к следующей задаче линейного программирования:
(1.2.3)
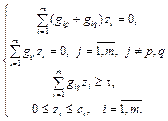(1.2.4)
Задача 1.1. Дорожная сеть состоит из транспортных узлов, соединенных между собой дорогами. Передвижение между узлами возможно лишь в одном направлении, разрешенные направления движения обозначены стрелками. Рядом с каждой стрелкой проставлены два числа: первое означает расстояние между узлами; второе (заключенное в скобки) – максимально возможную пропускную способность дороги (тыс.автомобилей в час).
Требуется:
| 1) найти наикратчайший путь проезда из пункта 1 в пункт 9; 2) найти критический (наиболее длинный) путь из пункта 1 в пункт 9; 3) определить максимальную пропускную способность дорожной сети |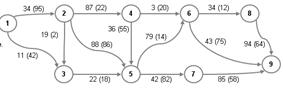 
|
Решение. Ответы на первый и второй вопросы находим, следуя (1.1.1)-(1.1.2). Реализуем следующие действия:
|
|
|
1) Из рисунка на рабочий лист вводим информацию по всем дугам сети (ячейки A35:D48 на шаблоне, рис.1.1 ниже);
2) перечисляем номера всех узлов сети (ячейки E34:M34);
3) вычисляем элементы матрицы инцидентности (ячейки E35:M48);
4) отводим столбец N35:N48 («выбор пути») под ячейки, которые будут определять искомый путь;
5) вычисляем итоги взаимодействия входящих в путь дуг со всеми узлами сети (ячейки E49:M49);
6) вычисляем суммарную длину всех дуг, образующих искомый путь (ячейка C49);
7) заносим в ячейки E50:M50 значения, определяющих сценарий пути (для начального узла пути заносим –1, для конечного узла заносим 1, для всех остальных заносим 0);
8) ставим задачу в «Поиске решения», отмечая при этом линейную модель, и решаем ее (рис.1.1):
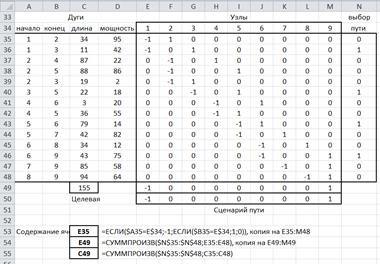
| Параметры Поиска решения: Установить целевую ячейку С49минимальному значению Изменяя ячейки N35:N48 Ограничения: Е49:М49 = Е50:М50 N35:N48 двоичное |
Рис.1.1. Шаблон с решением задачи 1.1 для ответа на первый вопрос
Для получения ответа на второй вопрос делаем копию листа рис. 1.1; вызываем «Поиск решения», целевую ячейку устанавливаем на максимальное значение; даем команду «выполнить» и получаем ответ на второй вопрос.
Для получения ответа на третий вопрос необходимо решить задачу по определению максимальной пропускной способности. Следуя (1.2.2)-(1.2.3), делаем следующие шаги:
1) копируем лист (рис. 1.1), где решалась задача определения пути минимальной длины;
2) на скопированном листе удаляем строку со сценарием пути и ячейку с длиной пути (рис. 1.2);
3) заголовок «выбор пути» над столбцом N35:N28 изменяем на заголовок «потоки» (рис. 1.2);
4) ставим задачу в «Поиске решения» и решаем ее (рис. 1.2):
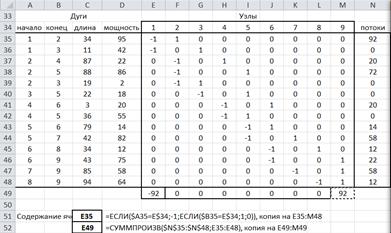
| Параметры Поиска решения: Установить целевую ячейку М49максимальному значению Изменяя ячейки N35:N48 Ограничения: F49:L49 = 0 N35:N48>=0 N35:N48 <= D35:D48 |
Рис. 1.2. Шаблон с решением задачи 1.1 для ответа на третий вопрос
2. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ (ИГРЫ ПРОТИВ ПРИРОДЫ)
Игрой против природы называется модель конфликта двух лиц, одно из которых не имеет цели, но своими действиями существенно влияет на качество принимаемых другим лицом решений. Такое лицо называется «природой». Другое лицо, имеющее цель и своими действиями стремящееся достичь ее, называется лицом, принимающим решения (ЛПР). Конечную игру против природы в нормальной форме задают с помощью платежной матрицы (матрицы исходов)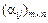 
, элементы которой являются выигрышами (проигрышами) ЛПР в ситуации 
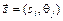. Здесь 
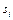– одно из решений ЛПР, а 
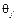– одно из состояний природы. Если в игре против природы элементы матрицы исходов 
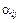являются выигрышами ЛПР, то такую матрицу называют матрицей выигрышей или матрицей полезности. В случае, когда 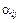представляют собой проигрыши ЛПР, матрица исходов называется матрицей проигрышей или матрицей потерь.
|
|
|
В зависимости от того, какая информация доступна ЛПР, а также от его субъективных характеристик (особенностей), при поиске оптимальных решений применяются различные критерии оптимальности.
|
|
|
