 |
Задачи для самостоятельного решения
|
|
|
|
Задача 3.1. Мелкооптовый продавецможет закупить несколько контейнеров огурцов, для их последующей распродажи в течение недели более мелкими партиями – ящиками. Розничной торговлей он не занимается. В каждом контейнере находится 100 ящиков с овощами. Общие издержки, связанные с приобретением, перевозкой, хранением и т.д. одного контейнера, составляют 70000 руб.; начальная продажная цена ящика со свежими овощами – 900 руб. Если в течение недели все огурцы не удается продать, то в самом конце недели оптовик реализует их остаток по сниженной цене – 300 руб. за ящик. Используя критерий ожидаемого значения (Байеса), определите, сколько контейнеров следует приобрести оптовику, чтобы получить максимум ожидаемой прибыли за недельный цикл, при условии, что вероятности спроса (количество ящиков с овощами, приобретаемых у оптовика в неделю по начальной цене) заданы в таблице:
| Количество ящиков | |||||||||
| 0,05 | 0,05 | 0,1 | 0,1 | 0,2 | 0,2 | 0,1 | 0,1 | 0,05 | 0,05 |
| Вероятности спроса |
Чему равна максимальная ожидаемая прибыль за недельный цикл?
Ответ: следует приобрести 5 контейнеров.Максимальная ожидаемая прибыль за недельный циклравна 61000 руб.
| Задача 3.2.Дорожная сеть состоит из семи транспортных узлов, соединенных между собой дорогами. Передвижение между узлами возможно лишь в одном направлении (движение однонаправленное); разрешенные направления движения обозначены стрелками. Числа, стоящие у стрелок, означают расстояние между узлами (км). Необходимо найти кратчайший и критический (самый длинный) пути проезда из узла 1 в узел 7. | 
|
Ответ: искомый кратчайший путь проходит через узлы 1-2-5-7. Его длина равна 14 км. Критический путь проходит через узлы 1-2-4-6-7. Его длина равна 25 км.
|
|
|
Задача 3.3. Дорожная сеть состоит из двенадцати транспортных узлов, соединенных между собой дорогами (рис. 3.1). Разрешенные направления движения обозначены стрелками. Числа, стоящие у стрелок, означают расстояние между узлами (км). Необходимо найти наикратчайший путь проезда из узла 1 в узел 12.
Рис. 3.1. Дорожная сеть
Ответ: кратчайший путь проходит через узлы 1-2-3-4-8-12. Его длина равна 27 км.
Задача 3.4. Для дорожной сети рис 3.1 найти кратчайшие пути проезда из пункта 12 в пункт 1 и из пункта 9 в пункт 4.
Ответ: кратчайший путь из пункта 12 в пункт 1 проходит через узлы 12-8-4-3-2-1; длина равна 32 км. Кратчайший путь из пункта 9 в пункт 4 проходит через узлы 9-5-1-2-3-4; длина равна 28 км.
Задача 3.5. Решить задачу 3.4 при условии, что пятый пункт закрыт для движения.
Ответ: кратчайший путь из пункта 12 в пункт 1 проходит через узлы 12-8-4-3-2-1; длина равна 32 км. Кратчайший путь из пункта 9 в пункт 4 проходит через узлы 9-10-11-7-3-4; длина равна 32 км.
Задача 3.6. Для дорожной сети на рис 3.2 найти кратчайший и критический пути проезда из пункта 1 в пункт 6.
Рис. 3.2. Дорожная сеть
Ответ: кратчайший путь проходит через узлы 1-2-6; длина равна 105 км. Критический путь проходит через узлы 1-5-4-2-3-6; длина равна 323 км.
Задача 3.7. Дорожная сеть (рис. 3.3) состоит из девяти транспортных узлов, соединенных между собой дорогами. Пропускные характеристики каждой из дорог (в тыс. автомобилей в час) в направлениях, указанных стрелками, заданы. Числа, стоящие рядом со стрелками, означают максимально возможную пропускную способность соответствующих дорожных участков в указанных направлениях. Требуется определить максимальную пропускную способность данной дорожной сети в целом, то есть, определить, какое максимальное число автомобилей может проехать за 1 час из начального узла 1 сети в ее конечный узел 9.
Рис. 3.3. Дорожная сеть
|
|
|
Ответ: максимальное значение для входного потока в контрольный 9-й узел сети – 12 тыс. автомобилей в час.
Задача 3.8. Сеть нефтепроводов состоит из девяти узлов, соединенных между собой трубами (рис. 3.4). Перекачка нефти между узлами возможна лишь в направлениях, указанных стрелками. Рядом с каждой из стрелок проставлены два числа, из которых одно заключено в скобки. То из чисел, которое не заключено в скобки, означает пропускную способность соответствующей трубы (у.е.). Число, заключенное в скобки, означает стоимость единицы потока по данной трубе (у.е.). Требуется найти распределение потоков по сети минимальной суммарной стоимости при условии, что суммарный приток в 9-й узел должен быть не менее 90 у.е.
Рис. 3.4. Сеть нефтепроводов
Задача 3.9. Для сети на рис. 3.4рассчитать ее максимальную пропускную способность между 1-м и 9-м узлами без учета стоимости потоков.
Задача 3.10. Решить задачу 3.8 при условии, что третий узел выведен из строя и прокачка нефти через него невозможна.
Задача 3.11. Решить задачу 3.8 при условии, что четвертый узел выведен из строя и прокачка нефти через него невозможна.
ДОМАШНЕЕ ЗАДАНИЕ
Разобрать приведенный ниже материал
СЕТЕВЫЕ ЗАДАЧИ
| Задача 1 (о замене).Транспортное агентство составляет 5-летний бюджетный план. В связи с этим возникает задача определения оптимальной стратегии замены автобусного парка. В табл. 1.1 приведены данные по стоимостям замен и годового обслуживания одного автобуса в зависимости от его возраста. Замены проводятся в конце очередного года. По окончании пятилетнего периода (в конце пятого года) все автобусы парка должны быть новыми. Требуется определить моменты замен старых автобусов на новые, при которых суммарная стоимость эксплуатации и затрат на замены за весь пятилетний период была бы минимальна. | Таблица 1.1
|
| Решение.Представим всю пятилетнюю операцию, связанную с эксплуатацией и заменами автобуса в виде сети, представленной на рис. 1.Кружок под номером N означает начало очередного N -го года рассматриваемого пятилетнего периода. Стрелка, ведущая из K -го в L -й кружок, означает операцию, состоящую в начале эксплуатации нового автобуса в начале K -го года и замену его на новый в начале L -го года. Число над стрелкой означает общую стоимость (тыс. руб.) такой операции, состоящей из эксплуатации автобуса в течение L-K лет и последующей его замены в конце этого срока на новый. |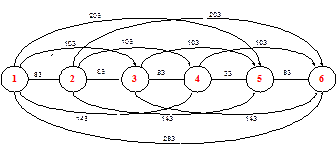 
Рис.1. Сеть процесса по эксплуатациям и заменам автобуса
|
В соответствии с приведенной схемой решение задачи сводится к определению кратчайшего пути между узлами 1 и 6, если в качестве длин дуг сети на рис. 1. взять проставленные рядом с ними стоимости соответствующих операций. Шаблон с решением представлен на рис. 2.
|
|
|
Рис. 2. Шаблон с решением задачи о замене
Из рис 1 видно, что искомый кратчайший путь проходит через узлы 1-4-6. Его длина равна 246. Это означает, что оптимальными заменами стали бы две – одна в начале четвертого года периода (после трех лет эксплуатации автобуса), а другая – в самом конце всего периода. Суммарная стоимость замен и эксплуатации при этом варианте составила бы 246 тыс. руб. На самом деле, существует еще один вариант с такой же общей стоимостью – замена в начале третьего года (после двух лет эксплуатации) и в конце (от перемены мест слагаемых сумма не меняется).
Задача 2. Задана дорожная сеть:
Рис. 3. Дорожная сеть
Передвижение между узлами возможно лишь направлениях, указанных стрелками. Числа, стоящие у стрелок, означают пропускные способности дорог (тыс. авт./час). Сеть подлежит ремонту, за счет которого планируется увеличить ее пропускную способность. Это будет достигнуто в результате модернизации некоторых сегментов сети. Стоимости модернизации (у.е.) дорожных сегментов (участков) сети, приводящих к увеличению их пропускных способностей на 1 тыс. авт. в час известны и заданы в таблицах:
| Дорожный участок | Стоимость модернизации | Дорожный участок | Стоимость модернизации | |||
| нач. узел | кон. узел | нач. узел | кон. узел | |||
|
|
|
1) Каким образом инвестировать100 у.е. средств в реконструкцию дорог (т.е. сколько денег вложить в ремонт того или иного дорожного участка, чтобы максимально увеличить пропускную способность маршрута «1»-«9»?
2) Определить минимальную сумму вложений в реконструкцию дорог, необходимую для достижения пропускной способности сети по маршруту «1»-«9» в 20 тыс. автомобилей в час.
Ответ на 1-й вопрос задачи: необходимо инвестировать (у.е.):
9,33 в модернизацию участка (1,2); 21,00 в модернизацию участка (1,3); 31,00 в модернизацию участка (2,5); 38,67 в модернизацию участка (5,9). Пропускная способность дорожной сети при этом увеличится до 31 тыс. автомобилей в час.
Ответ на 2-й вопрос задачи: необходимо инвестировать (у.е.):
15,00 в модернизацию участка (1,3); 3,00 в модернизацию участка (2,5); 16,00 в модернизацию участка (5,9). Минимальный суммарный объем инвестиций в модернизацию дорог, необходимый для достижения пропускной способности сети в 20 тыс. автомобилей в час равен 34,00 у.е.
|
|
|
