 |
Игры против природы. Рандомизированные решения
|
|
|
|
Рандомизированным решением 
ЛПР называется распределение вероятностей на множестве его обычных решений:
, 
, 
Критериями оптимальности для р.-решений служат те же критерии, что и рассмотренные выше критерии для обычных, нерандомизированных решений. Отличие лишь только в том, что при этом между собой сравниваются значения средних выигрышей (потерь), вычисляемые по формуле
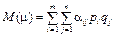(3)
где 
– вероятность свершения состояния 
природы.
Поиск оптимальных р.-решений по критерию Лапласа. Применяется при отсутствии какой-либо информации о вероятностях свершения состояний природы. Оптимальное по критерию Лапласа р.-решение находится из решения следующей задачи линейного программирования:
, (4)
,
Значения 
являющиеся компонентами оптимального плана задачи (4), и определяют искомое оптимальное р.-решение по критерию Лапласа.
Поиск оптимальных р.-решений по критерию ожидаемого значения (Байеса). Применяется, когда известны вероятности 
свершения всех состояний 
природы. Оптимальное р.-решение находится из решения задачи линейного программирования
, (5)
,
Значения являющиеся компонентами оптимального плана задачи (5), и определяют искомое оптимальное р.-решение по критерию ожидаемого значения (Байеса) при заданных вероятностях состояний природы.
Пример 4. В условиях примера 1 находим оптимальное р.-решение по критерию Байеса для заданных априорных вероятностей свершения состояний природы: 
. Следуя (5), для заданных значений элементов матрицы полезностей получаем задачу:
,
Полученную задачу линейного программирования решаем с помощью надстройки «Поиск решения» (рис. 4). В ответе получаем решение 
, означающее, что всю продукцию следует подвергнуть решению 
. Ожидаемое значение прибыли при этом равно 11,13.
|
|
|
Рис. 4. Шаблон с решением задачи примера 4
Поиск оптимальных р.-решений по критерию гарантированного результата (максимину и минимаксу). Данные критерии применяются тогда, когда необходимо получить гарантированный результат. В зависимости от того, является ли матрица исходов матрицей полезности или матрицей потерь, применяется либо критерий максимина (задача максимизации), либо критерий минимакса (задача минимизации). К ответу ведут решения следующих задач линейного программирования:
| критерий максимина: (для матрицы полезности): | критерий минимакса: (для матрицы потерь): |
 (6);
|  (7)
|
Пример 5. В условиях примера 1 находим оптимальное р.-решение по критерию максимина. Следуя (6), для заданных значений элементов матрицы полезностей получаем задачу:
Полученную задачу линейного программирования решаем с помощью надстройки «Поиск решения» (рис. 5).
Рис. 5. Шаблон с решением задачи примера 5
В ответе получаем решение 
, означающее, что четверть всей продукции следует подвергнуть решению , а три четверти – решению 
. Гарантированное среднее значение прибыли при этом равно 9.
Поиск оптимальных р.-решений по критерию Неймана-Пирсона. Критерий Неймана-Пирсона применяется тогда, когда природа может иметь всего два состояния, одно из которых находится под контролем. Пусть задана некоторая пороговая величина 
, и все р.-решения ЛПР, при которых его средние потери превышают порог (выигрыши меньше порога), отвергаются как недопустимые. Из всех допустимых р.-решений оптимальным по критерию Неймана-Пирсона объявляется то, при котором средние потери при неконтролируемом состоянии минимальны (выигрыш максимален). В зависимости от того, является ли матрица исходов матрицей полезности или матрицей потерь, получаем следующие задачи:
|
|
|
| (для матрицы полезности): | (для матрицы потерь): |
 область индексов допустимых решений;
 и  потери ЛПР при контролируемом и неконтролируемом состояниях соответственно.
| 
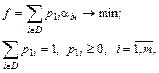
 область индексов допустимых решений;
и потери ЛПР при контролируемом и неконтролируемом состояниях соответственно.
|
|
|
|
