 |
Игры против природы. Нерандомизированные решения
|
|
|
|
Критерии гарантированного результата (максимин и минимакс). Данные критерии применяются тогда, когда необходимо получить гарантированный результат. Они соответствуют очень осторожному подходу, когда считается, что для любого решения ЛПР природой будет реализовано самое неблагоприятное для ЛПР состояние. Можно сказать, что критерии гарантированного результата соответствуют крайне пессимистичному ЛПР.
Оптимальное по критерию гарантированного результата решение находится из условия
(1)
Из (1) видно происхождение терминов «максимин» и «минимакс»: максимин соответствует случаю матрицы полезности и макси муму от мин имума (верхняя строка в (1)), а минимакс – случаю матрицы потерь мини мума от макс имума (нижняя строка в(1)).
Оптимальное по критерию гарантированного результата решение является, по-сути, защитной стратегией ЛПР в игре против природы.
Пример 1. Предприятие выпускает скоропортящуюся продукцию, которую может направить на продажу сразу (решение s 1), отправить на склад для хранения (решение s 2) или подвергнуть дополнительной обработке (решение s 3) для длительного хранения. Характер спроса на продукцию "Весны" определяется состоянием рынка; при этом предполагается, что возможны три состояния: продукция "Весны" приобретается немедленно (состояние ө1), в течение небольшого периода времени (состояние ө 2), после длительного периода времени (состояние ө 3). В случае решений s2 и s 3 предприятие несет дополнительные затраты на хранение и обработку продукции, которые не требуются при s 1, однако при s 1 следует учесть возможные убытки из-за порчи продукции, если состояние рынка будет ө2 или ө3. Матрица прибылей предприятия «Весна» задана в таблице:
|
|
|
| ө1 | ө2 | ө3 | |
| s 1 | |||
| s 2 | |||
| s 3 |
Решение. Для данной задачи критерием гарантированного результата является максимин (т.к. матрица исходов есть матрица полезности). В соответствии с (1) имеем:
; 
; 
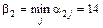, откуда 
. Оптимальным решением по критерию максимина является решение 
, обеспечивающее максимальное значение среднему гарантированному выигрышу ЛПР.
Критерий минимаксного сожаления (Сэвиджа). Реализуется за два шага.
Шаг 1. Вычисляется матрица сожалений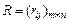 
по формулам
(2)
Элементы 
выражают собой сожаление ЛПР о том, что им в соответствующей ситуации выбрано не оптимальное решение.
Шаг 2. Искомое оптимальное по критерию Сэвиджа решение получается применением к полученной на шаге 1 матрице сожалений критерия минимакса.
Пример 2. В условиях примера 1 матрица сожалений принимает вид
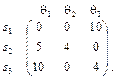
Применяя критерий минимакса, имеем 
; 
; 
, следовательно 
. Оптимальным решением по критерию Сэвиджа оказывается решение 
, обеспечивающее гарантированный минимум сожалений.
Критерий Гурвица. Критерий Гурвица охватывает весь спектр подходов ЛПР к принятию решений – от крайнего пессимизма до крайнего оптимизма. В рассмотрение вводится специальный числовой параметр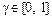 
, называемый параметром оптимизма. Перед принятием решения значение 
фиксируется. Оптимальное по критерию Гурвица решение 
выбирается из условия
Пример 3. В условиях примера 1 при показателе оптимизма 
, имеем
; 
;
.
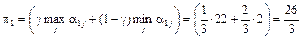Поскольку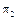 
является наибольшим, то оптимальным по критерию Гурвица решением с показателем оптимизма 
является решение .
Критерий Неймана-Пирсона. Применяется в ситуациях, когда состояние природы может принимать только два значения, причем одно из них более важно и находится под контролем. В рассмотрение вводится некоторая величина 
(порог), и все решения ЛПР, при которых его потери превышают порог (выигрыши меньше порога), отвергаются как недопустимые. Из всех допустимых решений оптимальным по критерию Неймана-Пирсона объявляется то, при котором потери при неконтролируемом состоянии минимальны (выигрыш максимален).
|
|
|
Пример 4. Предположим, что возможны два варианта уровня среднегодовых цен на нефть на мировом рынке на следующий год:
"высокий уровень цен на нефть"; 
"низкий уровень цен на нефть". Для простоты будем считать, что других состояний система мировых цен на нефть принимать не может.
Предположим далее, что некоторая нефтедобывающая компания разрабатывает стратегию своей работы на следующий год и может принять одно из трех следующих решений по добыче и экспорту нефти:
максимально нарастить добычу и экспорт нефти;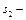 
оставить нефтедобычу и экспорт на текущем уровне;
максимально снизить уровень добычи и экспорта нефти.
Предположим, что потенциальные потери, которые определяются величиной упущенной прибыли при каждом из возможных сочетаний решений и состояний мировых цен на нефть, подсчитаны и задают следующую матрицу потерь:
.
Предположим далее, что контролируется состояние 
(низкие цены), а потери в этом состоянии не должны превысить порога 
. Тогда допустимыми решениями оказываются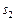 
и 
, из которых имеет меньшие потери при состоянии 
и, следовательно, является оптимальным по критерию Неймана-Пирсона с порогом .
|
|
|
