Определение функции и способы задания функции

Алгебра и начала математического анализа; геометрия

Методические указания

По выполнению контрольной работы

Для студентов 1 курса заочного отделения

Семестр

 

 

 

Заречный 2016

 

Голянова О.Н.

Математика: алгебра и начала математического анализа; геометрия. Методические указания по выполнению контрольной работы для студентов 1 курса заочного отделения. 2016. – стр.24

 

 

Методические указания содержат варианты заданий для контрольной работы по дисциплине «Математика: алгебра и начала математического анализа; геометрия», необходимые теоретические сведения, примеры решения типовых задач. Методические указания предназначены для студентов 1 курса заочной формы обучения по специальности 38.02.04 «Коммерция по отраслям» и составлена в соответствии с рабочей программой дисциплины.

 

 

Содержание

 

Раздел 1. Алгебра. 4

Тема 1.4. Функции, их свойства и графики. 4

1. Определение функции и способы задания функции. 4

2. Свойства функции. 5

3. Построение графиков линейной и квадратичной функций. 7

Раздел 2. Комбинаторика, статистика и теория вероятностей. 9

Тема 2.1. Элементы комбинаторики. 9

Тема 2.2. Элементы теории вероятностей. 11

Тема 2.3. Элементы математической статистики. 15

Задания для контрольной работы.. 17

 

Раздел 1. Алгебра

Тема 1.4. Функции, их свойства и графики

Определение функции и способы задания функции

 

Определение. Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция y=f(x) с областью определения Х.

Для области определения функции используют обозначение D(f). Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной. Множество всех значение функции y=f(x) называют областью значений функции и обозначают E(f).

Например, функция , где , есть отображение множества натуральных чисел в множество положительных рациональных чисел, так как каждому натуральному числу х формула ставит в соответствие вполне определенное положительное рациональное число . Все рассматриваемые нами функции будут определены, как правило на множестве R действительных чисел. Если при задании функции ее область определения не указывается, то при этом считают, что она определена для всех значений, для которых функция имеет смысл.

Пусть дана функция . Так как х и у принимают различные числовые значения, то они могут быть переменными, при этом х называют независимой переменной или аргументом, у – зависимой переменной или функцией.

Отношение, задающее функцию, может быть выражено различными способами. Например, одной формулой: ,

несколькими формулами:

или даже сопровождаться словесным пояснением: .

 

Пример 1. Вычислить значение функции при х =2.

Решение. Подставляем в заданное выражение для функции значение х=2.

.

 

Пример 2. Функция задана выражением

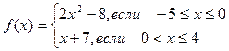Найти f(-1), f(0), f(3)

Решение. Значение х = -1 удовлетворяет условию -5≤х≤0, значит, f(-1) надо вычислять по формуле f(х)= 2х² – 8. Получим f(-1) = 2×(-1)² – 8 = -6.

Значение х = 0 удовлетворяет условию -5≤х≤0, значит, f(0) надо вычислять по формуле f(х)= 2х² – 8. Получим f(0) = 2×0² – 8 = -8

Значение х = 3 удовлетворяет условию 0<х≤4, значит, f(3) надо вычислять по формуле f(х) =х+7. Получим f(3) = 3 + 7 = 10.

 

Пример 3. Найти область определения функции .

Решение. Дробное выражение имеет смысл, если знаменатель отличен от нуля. При х =6 знаменатель дроби обращается в нуль, и следовательно, выражение не имеет смысла. Таким образом, .

Пример 4. Найти область определения функции .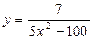

Решение. Дробное выражение имеет смысл, если знаменатель отличен от нуля. Найдем значения х, при которых знаменатель дроби обращается в нуль.

5х² – 100 = 0

5х² = 100

х² = 25

х₁ = -5 х₂ = 5

Таким образом, .

 

Функцию иногда можно представить таблицей, в первой строке которой перечисляются значения независимой переменной х, а во второй – соответствующие значения зависимой переменной. Запишем часть такой таблицы для функции :

х
у

Графиком функции называется множество всех точек координатной плоскости с координатами .

 

Свойства функции

 

Нули функции - это те значения аргумента х, при которых значение функции (y) равно нулю.

Чтобы найти нули функции y=f(x), нужно решить уравнение f(x)=0. Корни этого уравнения и будут нулями функции y=f(x).

Чтобы найти нули функции y=f(x) по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции.

Пример 5. Найти нули функции

Решение. Чтобы найти нули функции, решаем уравнение

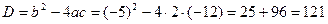
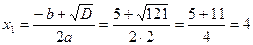
Итак, нули функции х₁ = 4, х₂ = -1,5.

 

Промежутки знакопостоянства функции y=f(x) - это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть f(x)>0 или f(x)<0.

Чтобы найти промежутки знакопостоянства функции y=f(x), нужно решить неравенства f(x)>0 и f(x)<0.

Чтобы найти промежутки знакопостоянства функции y=f(x) по ее графику, нужно:

- найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ - при этих значениях аргумента f(x)>0;

- найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ - при этих значениях аргумента f(x)<0.

Промежутки монотонности функции y=f(x) - это такие промежутки значений аргумента х, при которых функция y=f(x) возрастает или убывает.

Говорят, что функция y=f(x) возрастает на промежутке I, если для любых двух значений аргумента х₁, х₂, принадлежащих промежутку I таких, что

Другими словами, функция y=f(x) возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Чтобы по графику функции y=f(x) определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.

Говорят, что функция y=f(x) убывает на промежутке I, если для любых двух значений аргумента х₁, х₂, принадлежащих промежутку I таких, что х₁<х₂ выполняется соотношение: f(x₁)>f(x₂).

Другими словами, функция y=f(x) убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Чтобы по графику функции y=f(x) определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.

Четность и нечетность функции.

Функция y=f(x) называется четной, если выполняются для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение f(-x) = f(x). График четной функции симметричен относительно оси ОУ.

Функция y=f(x) называется нечетной, если выполняются для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение f(-x) = -f(x). График четной функции симметричен относительно начала координат (точки О(0, 0)).

Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.

Чтобы определить четность функции, нужно в уравнение функции y=f(x) вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду f(-x) или -f(x).

Если f(-x) = f(x), то функция четная. Если f(-x) = -f(x), то функция нечетная. Если не удалось привести ни к тому ни к другому, то наша функция y=f(x) - общего вида.

Пример 6. Задана функция . Определить, является ли функция четной или нечетной.

Решение. Находим у(-х).

Так как f(-x) =- f(x), то функция нечетная.

Функция называется периодической, существует такое положительное число Т, что для любого значения х из области определения функции выполняется равенство f(х+Т) = f(x) = f(x–T). Число Т называется периодом функции.

График периодической функции обладает следующей особенностью. Если Т – период функции у= f(х), то для построения ее графика достаточно построить ветвь графика на одном из промежутков длины Т, а затем выполнить параллельный перенос этой ветви вдоль оси на , , , …

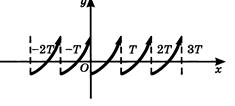
Рис.1. График периодической функции

Сложной функцией или композицией двух функций и называется функция . называется внутренней функцией, называется внешней функцией.

Пример 7. Заданы две функции , Найти композицию функций.

Решение. В заданную функцию подставляем заданное выражение для х, то есть .

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: