 |
Тема 2.1. Элементы комбинаторики
|
|
|
|
В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой.
Одним из основных понятий в комбинаторике является факториал.
Факториалом целого положительного числа n (обозначается n!) называется произведение 1∙2∙3∙…∙n = n!
Основное свойство факториала: n! = n*(n – 1)!.
Комбинаторные задачи – это задачи на перебор возможных вариантов.
Сочетаниями из n элементов по k называются их соединения, отличающиеся друг от друга только самими элементами. Число всех сочетаний из n различных элементов по k (обозначается  ):
):
 .
.
Основное свойство сочетаний:  .
.
Размещениями из n элементов по k называются такие соединения по k элементов, которые отличаются друг от друга самими элементами или их порядком. Число всех размещений из n различных элементов по k (обозначается  ):
): 
Перестановками из n элементов называются их соединения, отличающиеся друг от друга только порядком входящих в них элементов. Число всех перестановок из n различных элементов (обозначается Pn): Pn = n!.
Выбор формулы комбинаторики осуществляется по алгоритму

Пример 10. В группе 18 студентов. Сколькими способами можно выбрать 3 делегата на профсоюзную конференцию?
Решение.
По схеме получаем: n = 18, k = 3, порядок не важен. Используем формулу сочетаний.
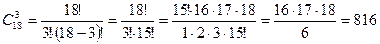
Ответ: 816 способов.
Пример 11. Правление фирмы выбирает 5 человек на различные должности из 16 кандидатов. Сколькими способами это можно сделать?
Решение.
По схеме получаем: n = 16, k = 5, порядок важен (должности различные). Используем формулу размещений.
|
|
|
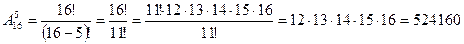
Ответ: 524 160 способов.
Пример 12. В студенческой группе 20 человек. Сколькими способами можно выбрать старосту и его заместителя?
Решение.
По схеме получаем: n = 20, k = 2, порядок важен (должность старосты и заместителя различны). Используем формулу размещений.

Ответ: 380 способов.
Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.
Правило суммы. Если некоторый объект А можно выбрать n способами, а другой объект В можно выбрать m способами, то выбор "либо А, либо В можно осуществить n+m способами.
Правило произведения. Если объект А можно выбрать n способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) m способами, то пары объектов А и В можно выбрать n×m способами.
Пример 13. Из 23 человек военнослужащих формируется караул, состоящий из начальника караула, его заместителя и трех караульных. Сколькими способами возможно сформировать такой караул?
Решение.
Сначала находим количество способов выбрать из 23 военнослужащих начальника караула и его заместителя. По схеме получаем: n = 23, k = 2, порядок важен (должность начальника караула и его заместителя различны). Используем формулу размещений.

Теперь находим количество способов выбрать из оставшихся военнослужащих трех караульных. По схеме получаем: n=23–2=21, k = 3, порядок не важен (все три караульных имеют одинаковую должность). Используем формулу сочетаний.

Тогда по правилу произведения получим
506×1330 = 672 980
Ответ: 672 980 способов.
Пример 14. Сколькими способами можно изготовить четырехцветных флажков, если использовать 10 цветов?
Решение.
По схеме получаем: n = 10, k = 4, порядок важен (все цвета различны и могут располагаться в разном порядке). Используем формулу размещений.
|
|
|

Ответ: 5040 способов
Пример 15. В отделе работают 8 мужчин и 5 женщин. Сколькими способами можно составить группу из 4 человек так, чтобы в ней было не менее 3 мужчин?
Решение
Группа должна состоять из 4 человек, из них не менее 3 мужчин, то есть возможны случаи: в группе 3 мужчины и 1 женщина или все 4 мужчины.
1-й случай – в группе 3 мужчины и 1 женщина.
Число способов выбрать 3 мужчин из 8 имеющихся в отделе равно числу сочетаний

Число способов выбрать одну женщину из 5 имеющихся в отделе равно

Тогда по правилу произведения получим 56×5=280
2-й случай – в группе 4 мужчины.
Число способов выбрать 4 мужчин из 8 имеющихся в отделе равно числу сочетаний

По правилу суммы имеем
280 + 70 = 350
Ответ: 350 случаев
|
|
|


