 |
Тема 2.2. Элементы теории вероятностей
|
|
|
|
Наблюдаемые события можно разделить на три вида: достоверные, невозможные и случайные.
Событие называется достоверным, если оно обязательно произойдет при выполнении данного ряда условий.
Событие называется невозможным, если оно заведомо не произойдет при выполнении данного ряда условий.
Событие называется случайным, если при осуществлении ряда условий оно может либо произойти, либо не произойти.
Испытанием называется осуществление ряда условий.
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
Очевидно, единственно возможные события являются попарно несовместимыми.
События называются равновозможными, если можно считать, что ни одно из них не является более возможным, чем другие.
Элементарным исходом называется каждый из возможных результатов испытания.
Полной группой называется совокупность единственно возможных событий испытания.
Противоположными называются два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое обозначают A.
Суммой A + B двух событий A и B называется событие, состоящее в появлении события A или события B, или обоих этих событий.
Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.
Произведением двух событий A и B называется событие AB, состоящее в совместном появлении этих событий.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
|
|
|
Вероятностью события А называется отношение числа благоприятных исходов к общему числу всех элементарных исходов испытания, если все исходы равновозможны (классическое определение вероятности).
Формулой это определяется так: 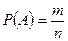
где m – число элементарных исходов, благоприятных событию A; n – число всех возможных элементарных исходов.
Из определения вероятности вытекают следующие свойства:
а) вероятность достоверного события равна единице;
б) вероятность невозможного события равна нулю;
в) вероятность случайного события есть положительное число, заключенное между нулем и единицей;
г) вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Пример 16. Структура занятых в региональном отделении крупного банка дана в таблице:
| Структура | женщины | мужчины |
| Администрация | 10 | 7 |
| Операторы | 12 | 15 |
Случайно отобран один служащий. Какова вероятность того, что он: а) женщина-оператор; б) мужчина-администратор; в) женщина; г) администратор?
Решение
а) Событие А – отобранный служащий женщина-оператор
 . Имеем m=12 (количество женщин-операторов); всего служащих n=10+7+12+15=44
. Имеем m=12 (количество женщин-операторов); всего служащих n=10+7+12+15=44
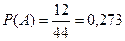
б) Событие В – отобранный служащий мужчина-администратор
Количество мужчин-администраторов равно m=7. 
в) Событие С – отобранный служащий женщина
Количество женщин равно m=10+12=22. 
г) Событие D – отобранный служащий администратор
Количество администраторов равно m=10+7=17. 
Ответ: а) 0,273 б) 0,159 в) 0,5 г) 0,386
Пример 17. В коробке 20 неразличимых конфет, из которых 9 с шоколадной начинкой и 11 с фруктовой. Берут наугад две конфеты. Какова вероятность того, что обе конфеты с шоколадной начинкой?
Решение. Событие А – из двух взятых конфет обе конфеты с шоколадной начинкой.
Число способов выбрать 2 конфеты с шоколадной начинкой из имеющихся 9 равно

Число способов выбрать любые две конфеты из имеющихся 20 равно
|
|
|
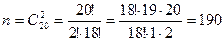
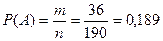
Ответ: 0,189
Пример 18. Среди 25 билетов 5 выигрышных. Найти вероятность того, что среди трех выбранных наугад хотя бы один выигрышный.
Решение
Событие А – из трех выбранных билетов хотя бы один выигрышный.
Событие  – противоположное событие - из трех выбранных билетов ни одного выигрышных, т.е. все три без выигрыша.
– противоположное событие - из трех выбранных билетов ни одного выигрышных, т.е. все три без выигрыша.
Всего билетов 25, среди них 5 выигрышных, значит, без выигрыша 25 – 5 = 20 билетов.

Так как сумма вероятностей противоположных событий равна 1, то

Ответ: 0,504
Условной вероятностью P(B|A) называется вероятность события В, вычисленная в предположении, что событие А уже произошло.
Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
P(AB) = P(A)×P(B | A) = P(В)×P(А | В).
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
P(A1A2 A3...A n) = P(A1)×P(A2 | А1)×P(A3 | A1A2)×...×P(An | A1 A2...An-1).
Два события А и В называются независимыми, если
P(AB) = P(A)×P(B).
Теорема. Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
P(A1 + A2 +... + An) = P(A1) + P(A2) +... + P(An).
Теорема. Сумма вероятностей событий A 1, A 2,..., A n, образующих полную группу, равна единице:
P(A1) + P(A2) +...+ P(An) = 1.
Теорема. Сумма вероятностей противоположных событий равна единице:
P(A) + P(A) = 1.
Пример 19. В двух урнах находятся шары, отличающиеся только цветом. В первой урне: 7 белых шаров, 8чёрных и 12 красных. Во второй урне 8 белых шаров, 11чёрных и 15 красных. Из каждой урны наудачу извлекаются по одному по одному шару. Какова вероятность того, что извлечённые шары будут одинакового цвета?
Решение
I урна: 7 белых, 8 черных и 12 красных шаров. Всего 27 шаров.
II урна: 8 белых, 11 черных и 15 красных шаров. Всего 34 шара.
Событие А – извлеченные шары одинакового цвета.
Событие В1 – из каждой урны извлекли белый шар
Событие В2 – из каждой урны извлекли черный шар
Событие В3 – из каждой урны извлекли красный шар
|
|
|


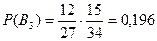
Так как события В1, В2 и В3 несовместны, то
Р(А) = Р(В1) + Р(В2) + Р(В3) = 0,061 + 0,096 + 0,196 = 0,353
Ответ: 0,353
Пример 20. В электрическую цепь последовательно включены два элемента, работающих независимо друг от друга. Вероятности отказов элементов равны соответственно q1=0,12 и q2=0,17. Найти вероятность того, что тока в цепи не будет.
 Решение.
Решение.
q1 = 0,12 – вероятность отказа первого элемента, тогда p1 = 1 – 0,12 = 0,88 – вероятность работы первого элемента.
q2 = 0,17 – вероятность отказа второго элемента, тогда p2 = 1 – 0,17 = 0,83 – вероятность работы второго элемента.
Событие А – тока в цепи не будет.
Событие  - противоположное событие - ток в цепи будет. При последовательном соединении ток в цепи будет, если оба элемента работают, т.е.
- противоположное событие - ток в цепи будет. При последовательном соединении ток в цепи будет, если оба элемента работают, т.е.

Так как сумма вероятностей противоположных событий равна 1, то

Ответ: 0,2696
Пример 21. Вероятность поражения цели первым стрелком равна р1=0,83, а вторым р2=0,78. Оба стрелка стреляют одновременно. Найти вероятность поражения цели.
Решение
Событие А – цель поражена, т.е. попал хотя бы один стрелок.
Событие  - противоположное событие – оба стрелка промахнулись (цель не поражена).
- противоположное событие – оба стрелка промахнулись (цель не поражена).
р1 = 0,83 – вероятность поражения цели первым стрелком, тогда q1 = 1 – 0,83 = 0,17 – вероятность промаха первым стрелком.
р2 = 0,78 – вероятность поражения цели вторым стрелком, тогда q2 = 1 – 0,78 = 0,22 – вероятность промаха вторым стрелком.

Так как сумма вероятностей противоположных событий равна 1, то
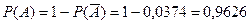
Ответ: 0,9626
Пример 22. Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна р1=0,16; второй р2=0,18; третий р3=0,2. Найти вероятность того, что:
а) в течение часа потребует вмешательства наладчика только один станок;
б) в течение часа потребует вмешательства наладчика все три станка.
Решение
р1 = 0,16 q1 = 1 – 0,16 = 0,84
р2 = 0,18 q2 = 1 – 0,18 = 0,82
р3 = 0,2 q2 = 1 – 0,2 = 0,8
1) Событие А – в течение часа потребует вмешательства наладчика только один станок
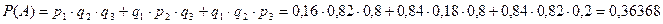
2) Событие В – в течение часа потребует вмешательства наладчика все три станка
|
|
|

Ответ: а) 0,36368; б) 0,00576
Пример 23. В ящике 20 деталей, среди которых 8 бракованных. Наудачу достают 3 детали. Найти вероятность следующих событий:
а) все детали окажутся годными;
б) две детали окажутся годными и одна бракованная.
Решение
n = 20 – всего деталей m = 8 – число бракованных деталей
20 – 8 = 12 – число годных деталей
а) Событие А – из трех взятых деталей все детали годные.



б) Событие В – из трех взятых деталей две детали окажутся годными и одна бракованная.


Ответ: а) 0,193; б) 0,049
|
|
|


