 |
Классическое определение вероятности
|
|
|
|
Элементы комбинаторики
Пусть а и b – элементы конечного множества.
Правило 1 (сложения). Если элемент а может быть выбран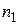 
способами, а элемент b – 
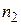способами, причем первые и вторые способы не пересекаются, то любой из элементов (а или b) можно выбрать 
способами.
Правило 2 (умножения). Если элемент а может быть выбран 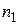способами, а элемент b – 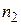способами, то оба элемента (а и b) в указанном порядке можно выбрать 
способами.
Схема выбора без возвращений
Пусть дано множество, состоящее из n различных элементов.
Размещением из n элементов по m элементов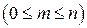 
называется любое упорядоченное подмножество данного множества, содержащее m элементов.
Два размещения различны, если они отличаются друг от друга либо составом элементов либо порядком их расположения, и обозначаются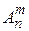 
.
Перестановкой из n элементов называется размещение из n элементов по n элементов. Число перестановок из n элементов обозначается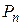 
.
Сочетанием из n элементов по m 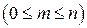называется любое подмножество данного множества, которое содержит m элементов.
Два сочетания различны, если они отличаются хотя бы одним элементом, и обозначаются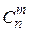 
.
Схема выбора с возвращением
Если при упорядоченной выборке m элементов из n элементов возвращаются обратно, то получаем размещения с повторениями. Число всех размещений с повторениями из n элементов по m обозначается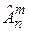 
.
Если при выборке m элементов из n элементы возвращаются обратно без последующего упорядочивания (то есть одни и те же элементы могут выниматься несколько раз, поэтому повториться), то полученные выборки есть сочетания с повторениями. Число всех сочетаний с повторениями из n элементов по m обозначается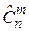 
.
Пусть в множестве из n элементов есть m различных элементов, при этом первый элемент повторяется 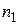раз, второй – 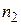раз, …, m -ый – 
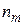раз, причем 
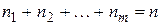. Тогда перестановки элементов данного множества представляют собой перестановки с повторениями и обозначаются 
.
|
|
|
Формулы для вычислений приведены в таблице (первая строка без повторений, вторая с повторениями).
| Размещения | Перестановки | Сочетания | |
| 
| 
| |
| 
| 
|
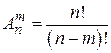
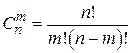
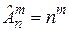
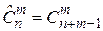
Пример 1. В ящике 100 деталей. Известно, что 50 из них – 1 сорта, 20 –
2-го, остальные – 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2 -го сорта?
Решение. Деталь 1-го сорта может быть извлечена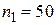 
способами, 2-го сорта – 
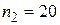способами. По правилу суммы существует 
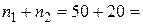= 70 способов извлечения одной детали первого или второго сорта.
Пример 2. Порядок вступления 12 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Каждый вариант отличается только порядком участников, т.е. перестановкой
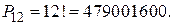
Пример 3. Сколькими способами можно переставить буквы в слове ЛИМПОПО?
Решение. Букв всего 7, но среди них 2 буквы О и 2 буквы П, поэтому вычисляем по формуле перестановок с повторениями
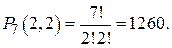
Пример 4. В магазине есть 7 видов тортов. Сколькими способами можно составить набор, содержащий три торта?
Решение. Имеем выборку с повторением из 7 элементов по 3, причем важен только состав.
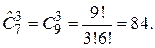
Пример 5. Пять человек вошли в лифт на 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
Решение. Каждый из 5 пассажиров может выйти на любом из 8 этажей. Имеем выборку с повторением, где важен и порядок и состав. Итак,
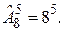
Пример 6. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?
Решение. Имеем выборку без повторения из 10 элементов по 7, в которой важен только состав. То есть
|
|
|
.
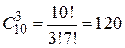Классическое определение вероятности
Случайные события обозначаются латинскими буквами А, В, С, …. Достоверное событие обозначим через Е, невозможное – символом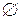 
. Равенство А = В означает, что появление одного из этих событий влечет за собой появление другого.
Произведение событий А и В есть событие С = АВ, состоящее в наступлении обоих событий А и В.
Сумма событий А и В есть событие С = А+В, состоящее в наступлении хотя бы одного из событий А и В.
Разность событий А и В есть событие С = А–В, состоящее в том, что А происходит, а В не происходит.
Противоположное событие обозначается той же буквой. но с чертой сверху (событие А;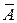 
– противоположное). Если А происходит, то 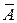– не происходит.
События А и В несовместны, если АВ = .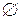
События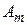 
(m = 1,2,…, n) образуют полную группу, если в результате опыта обязательно должно произойти хотя бы одно из них; при этом 
.
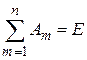Если результат опыта можно представить в виде полной группы событий, которые попарно несовместны и равновозможны, то вероятность события равна отношению числа 
благоприятствующих этому событию исходов опыта к общему числу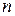 
всех возможных исходов, т.е. 
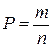; под равновозможными понимаются события, которые в силу тех или других причин не имеют объективного преимущества одно перед другим.
Пример 1. Из 30 студентов 10 имеют спортивные разряды, какова вероятность того, что выбранные наудачу три студента – разрядники?
Решение. Событие А – 3 наудачу выбранных студента – разрядники. Общее число выбора 3 студентов из 30 представляет собой выборку без повторения, в которой важен только состав, т.е.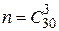 
. Аналогично число благоприятствующих событию А исходов опыта 
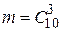. Итак,
.
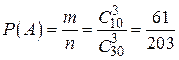Пример 2. На склад поступило N изделий, среди которых M бракованных. Определить вероятность того, что среди 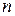наугад взятых со склада изделий окажется бракованных.
Решение. Выбрать 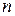изделий из N можно 
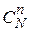способами. Число способов выбора бракованных из M равно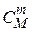 
, причем каждый из них может быть дополнен (n – m) изделий из общего числа стандартных изделий (N–M) числом способов 
. Таким образом,
.
§3. Теоремы сложения и умножения вероятностей.
Условная вероятность
Вероятность суммы двух событий определяется по формуле
|
|
|
.
Для несовместных событий вероятность суммы событий равна сумме вероятностей событий
.
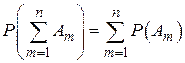Условной вероятностью 
события А называется вероятность появления этого события, вычисленная в предположении, что событие В уже произошло. События А и В независимы, если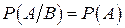 
.
Вероятность произведения двух событий определяется по формуле
.
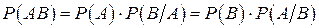Пример 1. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Определить вероятность хотя бы одного попадания в мишень.
Решение. Пусть событие А – попал первый стрелок. Событие В – попал второй стрелок, тогда
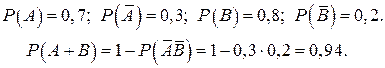
Пример 2. Вероятность поражения мишени для стрелка равна 
. Если при первом выстреле зафиксировано попадание, то стрелок получает право выстрела по второй мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,5. Определить вероятность поражения второй мишени.
Решение. Пусть А – поражение первой мишени, В – поражение второй мишени, тогда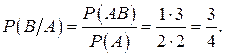 
Пример 3. Вероятность, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность, что студентом будет сдан: а) только первый экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Решение. Пусть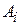 
– студент сдаст i -ый экзамен 
.
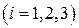а) В – студент сдаст только первый экзамен, тогда
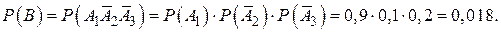
б) С – студент сдаст только один экзамен
в) Событие D – студент сдаст все три экзамена
.
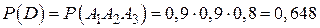г) Событие Е – студент сдаст по крайней мере два экзамена
.
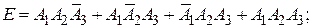
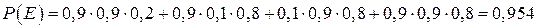д) Событие F – студент сдаст хотя бы один экзамен
|
|
|
