 |
Показательное распределение
|
|
|
|
Если плотность распределения вероятностей случайной величины задана функцией

тогда случайная величина распределена по показательному (экспоненциальному) закону. Для показательного закона верно:

Если Т – время безотказной работа механизма, то 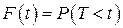 выражает вероятность входа из строя механизма за время t. Тогда
выражает вероятность входа из строя механизма за время t. Тогда  – вероятность безотказной работы механизма за время t. Функция
– вероятность безотказной работы механизма за время t. Функция  называется функцией надежности
называется функцией надежности  , где
, где  – число отказов в единицу времени.
– число отказов в единицу времени.
Пример 5. Время безотказной работы прибора подчинено показательному закону с плотностью распределения вероятностей 
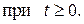 Найти вероятность того, что прибор проработает безотказно 100 часов.
Найти вероятность того, что прибор проработает безотказно 100 часов.
Решение. По условию  Искомая вероятность
Искомая вероятность
 .
.
Нормальный закон распределения
Плотность вероятности нормального распределения случайной величины имеет вид:
 ,
,
где а – математическое ожидание,  – среднее квадратическое отклонение нормально распределенной случайной величины.
– среднее квадратическое отклонение нормально распределенной случайной величины.
Для нормального распределения верно
 ,
,
где  – функция Лапласа,
– функция Лапласа,  .
.
Для нормального распределения верны формулы:

Пример 6. Измерение дальности до объекта сопровождается систематическими (математическое ожидание) и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчинены нормальному закону со средним квадратическим отклонением  . Найти вероятность измерения дальности с ошибкой не превосходящей по абсолютной величине 150 м.
. Найти вероятность измерения дальности с ошибкой не превосходящей по абсолютной величине 150 м.
Решение. Пусть Х – суммарная ошибка измерения дальности. Ее систематическая составляющая а = –50 м, поэтому имеем

Пример 7. Средняя масса коробки конфет равна 540 г. Найти  , если известно, что масса коробок распределена нормально и 5 % коробок имеют массу не большую 530 г.
, если известно, что масса коробок распределена нормально и 5 % коробок имеют массу не большую 530 г.
|
|
|
Решение. По условию а = 540,  так как
так как  , то
, то 



Неравенство Чебышева
Пусть у случайной величины Х определено 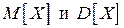 , то для любого
, то для любого  верно неравенство:
верно неравенство:
 .
.
Для относительной частоты  события А в п независимых испытаниях, в каждом из которых оно может произойти с вероятностью р, неравенство Чебышева примет вид
события А в п независимых испытаниях, в каждом из которых оно может произойти с вероятностью р, неравенство Чебышева примет вид
 .
.
Пример 1. Игральная кость подбрасывается 1200 раз. Оценить вероятность отклонения относительной частоты выпадения 6 очков от вероятности этого события (по модулю) на величину, меньшую, чем 0,02.
Решение. Исходя из неравенства Чебышева, имеем
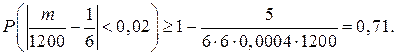
Пример 2. Всхожесть семян некоторой культуры равна 0,85. Оценить вероятность того, что из 400 посеянных семян число взошедших будет заключено в пределах от 300 до 380.
Решение. Случайная величина Х – число взошедших семян имеет биноминальное распределение 
 . Тогда по неравенству Чебышева имеем
. Тогда по неравенству Чебышева имеем

Решение типовых задач
Задача 1. В группе 30 человек. Необходимо выбрать старосту, заместителя и профорга. Сколько существует способов это сделать?
Решение. Старостой может быть выбран любой из 30 человек, заместителем – любой из оставшихся 29, а профоргом – любой из оставшихся 28. По правилу умножения имеем  способов. Задачу можно решить иначе. Мы имели выборку 3 элементов из 30 без возвращения, которые отличаются и порядком и составом, поэтому
способов. Задачу можно решить иначе. Мы имели выборку 3 элементов из 30 без возвращения, которые отличаются и порядком и составом, поэтому
 .
.
Задача 2. В шахматном турнире участвуют 10 гроссмейстеров, 6 международных мастеров и 4 мастера. Шахматисты для первого тура и номер столиков для каждой пары участников определяются путем жеребьевки. Найти вероятность того, что за первым столиком встретятся шахматисты одной и той же категории.
Решение. Число всех равновозможных случаев определения двух соперников из 20 участников равно числу сочетаний из 20 элементов по 2, т.е.  Число групп по 2 человека, которые могут быть составлены из 10 гроссмейстеров, равно
Число групп по 2 человека, которые могут быть составлены из 10 гроссмейстеров, равно  Число групп, которые могут быть составлены из 6 международных мастеров, равно
Число групп, которые могут быть составлены из 6 международных мастеров, равно  Из 4 мастеров может быть составлено
Из 4 мастеров может быть составлено  пар. Сумма
пар. Сумма  равна числу благоприятных случаев для встречи за первым столиком шахматистов одной и той же категории. Следовательно, искомая вероятность
равна числу благоприятных случаев для встречи за первым столиком шахматистов одной и той же категории. Следовательно, искомая вероятность  .
.
|
|
|
Задача 3. На стеллаже библиотеке в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А).
Решение. Первый способ. Требование – хотя бы один из трех учебников в переплете – будет осуществлено, если произойдет любое из следующих трех несовместных событий: В – один учебник в переплете, С – два учебника в переплете, D – три учебника в переплете.
Интересующие нас события А можно предоставить в виде суммы событий: А=В+С+D. По теореме сложения,
Р (А) =Р (В) +Р (С)+ Р (D). (*)
Найдем вероятность событий В, С и D:

Подставив эти вероятности в равенство (*), окончательно получим
Р (А) = 45/91+20/91+2/91=67/91.
Второй способ. Событие А (хотя бы один из взятых трех учебников имеет переплет) и  (ни один из взятых учебников не имеет переплета) – противоположные, поэтому
(ни один из взятых учебников не имеет переплета) – противоположные, поэтому  Отсюда
Отсюда 
Вероятность появления события 
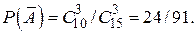
Искомая вероятность

Задача 4. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60 % деталей отличного качества, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение. Обозначим через А событие – деталь отличного качества. Можно сделать два предположения (гипотезы):  – деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй)
– деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) 
 – деталь произведена вторым автоматом, причем
– деталь произведена вторым автоматом, причем  .
.
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом,  .
.
Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом,  .
.
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятность равна
|
|
|
 ого качества, а второй - 84%мат ир.
ого качества, а второй - 84%мат ир.
Искомая вероятность того, что взятая деталь произведена первым автоматом, по формуле Байеса равна
 .
.
Задача 5. Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождевых дней. Найти вероятность того, что из случайно зафиксированных в этом месяце 8 дней дождливыми окажутся: а) три дня; б) не менее трех дней; в) не более трех дней.
Решение. Наблюдения в условиях данной задачи являются независимыми. Вероятность выпадение дождя в любой день сентября р = 12/30 = 0,4, а вероятность того, что в любой день сентября дождя не будет, q = 1 –р = 1–0,4 = 0,6.
Вероятность  того, что в n наблюдениях событие наступит m раз, определяется формулой биноминального распределения (формулой Бернулли).
того, что в n наблюдениях событие наступит m раз, определяется формулой биноминального распределения (формулой Бернулли).
а) По условию задачи n = 8, m = 3, p = 0,4, q = 0,6. Тогда
 .
.
б) Поскольку n = 8,  , то
, то
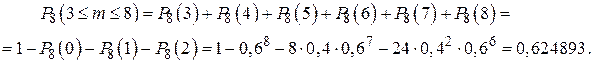
в) Так как n = 8, 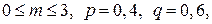 то
то

Задача 6. На факультете 730 студентов. Вероятность дня рождения каждого студента в данный день равна 1/365. Вычислить вероятность того, что найдутся 3 студента, у которых дни рождения совпадают.
Решение. В данном случае n = 730, m = 3, p = 1/365, q = 1–1/365 = 364/365. Так как n велико, воспользуемся локальной теоремой Муавра – Лапласа:
 где
где 
Имеем:

Задача 7. Проводится четыре независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Рассматривается случайная величина Х – число появления события А в четырех опытах. Записать закон распределения СВ Х. Вычислить математическое ожидание 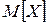 .
.
Решение. Случайная величина Х может принимать следующие значения:  Вероятности
Вероятности  вычисляются по формуле Бернулли:
вычисляются по формуле Бернулли:

В результате вычислений получим закон распределения в виде следующей таблицы:

| |||||

| 0,1296 | 0,3456 | 0,3456 | 0,1536 | 0,0256 |
Далее находим:

Задача 8. Дана функция распределения СВ Х

Найти плотность распределения вероятностей f (x), математическое ожидание 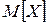 , дисперсию D [ X ] и вероятность попадания СВ Х на отрезок [1,2].
, дисперсию D [ X ] и вероятность попадания СВ Х на отрезок [1,2].
Решение. Так как 

Далее вычисляем:
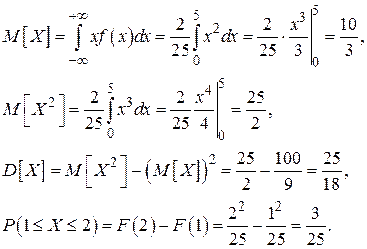
Задача 9. Случайная величина Х распределена нормально с математическим ожиданием а = 12,5. Вероятность попадания СВ Х в интервал (10;15) равна 0,2. Чему равна вероятность попадания СВ Х в интервал (35;40)?
|
|
|
Решение. Для нормального распределения верна формула

Находим:

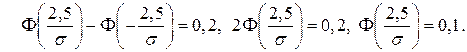
Т.к.  то
то 


Задача 10. Дан закон распределения дискретной случайной величины Х
| Х | 
| |||
| P | 0,4 | р | 0,1 | 0,2 |
Найти значение р, математическое ожидание 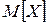 и дисперсию D [ X ].
и дисперсию D [ X ].
Решение. Т.к.  то 0,4 + р + 0,1 + 0,2 = 1. Отсюда, р = 0,3.
то 0,4 + р + 0,1 + 0,2 = 1. Отсюда, р = 0,3.
Найдем математическое ожидание Х:

Найдем математическое ожидание  :
:

Найдем дисперсию Х:

Задача 11. Для непрерывной случайной величины Х задана плотность распределения

Найти: а) параметр  , б) математическое ожидание, дисперсию,
, б) математическое ожидание, дисперсию,  .
.
Решение. а) Так как 


Задача 12. Вероятность некоторого события в каждом испытании из серии 9000 независимых испытаний равна 1/3. Используя неравенство Чебышева, оценить вероятность того, что частота этого события отклонится от его вероятности по абсолютной величине не более чем на 0,01.
Решение: Неравенство Чебышева для СВ Х имеет вид

Для данной задачи неравенство Чебышева записывается в виде

где
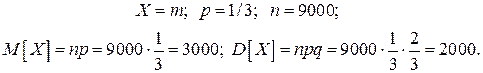
Тогда 
Таким образом, согласно неравенству Чебышева, имеем оценку





































Редактор Л.И. Чигвинцева
Компьютерная верстка О.Г. Белименко
ИД № 06039 от 12.10.2001
Свод. темплан 2010 г.
Подписано в печать 15.01.2010. Формат 60х84 1/16. Отпечатано на дупликаторе.
Бумага офсетная. Усл. печ. л. 5,25. Уч.-изд. л. 5,25. Тираж 150 экз. Заказ 60.
 |
Издательство ОмГТУ. Омск, пр. Мира, 11. Т. 23-02-12
|
|
|


