 |
Свойства математического ожидания
|
|
|
|
1. 
,
2. 
,
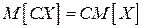3. 
,
4. 
, если случайные величины X и Y независимы.
Дисперсией или рассеянием 
случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
.
Величина 
называется средним квадратическим отклонением случайной величины Х.
Для непрерывных случайных величин
.
Основные свойства дисперсии
1. 
,
2. 
,
3. 
,
4. 
.
Пример 1. Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом 5 изделий для проверки их качеств. Построить ряд распределения случайного числа Х – дефектных изделий содержащихся в выборке. Найти математическое ожидание и дисперсию.
Решение. Значения случайной величины принимают значения 
Вероятность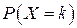 
вычислим по формуле
В результате получим
| ||||||
| 0,583 | 0,340 | 0,070 | 0,007 |
.
.
Пример 2. Производятся последовательные независимые испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайного числа испытанных приборов, если вероятность выдержать испытания для каждого из них равна 0,9. Найти математическое ожидание и дисперсию.
Решение. Значения случайной величины есть 
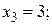
А их вероятности будут иметь значения
и ряд имеет вид
|
| |||||
|
| 0,1 | 0,09 | 0,081 | 0,0729 | 0,6561 |
,
Пример 3. Непрерывная случайная величина Х задана функцией распределения 
. Найти: а) плотность распределения 
; б) математическое ожидание, дисперсию; в) вероятность 
.
.
Решение. а) Плотность вероятности
б) Математическое ожидание и дисперсию непрерывной случайной величины найдем по формулам
|
|
|
в) Вероятность попадания случайной величины Х на промежуток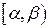 
вычислим по одной из формул
Основные законы распределения случайных величин.
Биномиальный закон распределения
Пусть в каждом из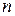 
независимых испытаний событие А появляется с вероятностью 
. Тогда случайная величина Х, означающая число появлений события А в 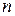независимых испытаниях, может принимать значения 0,1,2,…, 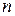с вероятностями
.
Такое распределение называется биноминальным. Здесь имеем
Пример 1. Найти среднее число лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, а вероятность выигрыша одного билета равна 0,1. Найти дисперсию числа успехов в данном опыте.
Решение. 
Распределение Пуассона
Если число испытаний велико, а вероятность р появления события А мала, то
где m – число появления события А в 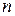независимых испытаниях; a = np. Для распределения Пуассона 
. Если a выражает число появлений события за единицу времени, то вероятность наступления 
событий за время t определяется формулой Пуассона
.
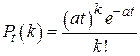Пример 2. Среднее число машин, прибывающих в автопарк за 1 минуту, равно двум. Найти вероятность того, что за 5 минут прибудет не менее двух машин.
Решение. 
,
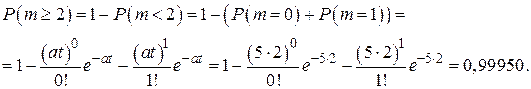
Гипергеометрическое распределение
Дискретная случайная величина Х имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения 
с вероятностями 
, где 
– натуральные числа; известно, что
.
Пример 3. В сетке 8 баскетбольных мячей, из которых 6 уже были использованы для игр. Для очередной игры отобрали 2 мяча, а после игры положили опять в сетку. Найти закон распределения и числовые характеристики случайной величины Х, равной числу оставшихся после игры новых мячей.
Решение. Первоначально в сетке было 2 новых мяча, а после игры их может остаться 0 или 1 или 2:
, 
.
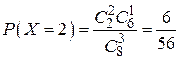| Х | |||
| Р | 
| 
| 
|
, 
.
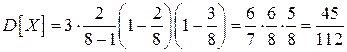Равномерное распределение
|
|
|
Если случайная величина Х принимает все значения 
с постоянной плотностью распределения вероятностей 
, то говорят, что случайная величина Х распределена равномерно на отрезке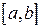 
. Плотность равномерно распределенной случайной величины Х
Известно, что 
Пример 4. Поезда метро идут с интервалом в 2 минуты. Найти вероятность того, что пассажир, пришедший на станцию, будет ожидать поезд менее 30 секунд.
Решение. Пусть случайная величина Х – время прихода пассажира на станцию. Очевидно, что Х – равномерно распределена на интервале 
. Функция распределения имеет вид: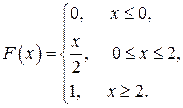 
Отсюда 
|
|
|
