 |
Глава 1. Теоретические предпосылки влияния эффекта Холла на ЗС
|
|
|
|
Эффект Холла был открыт Эдвином Гербертом Холлом в 1879 году в тонких пластинках золота [57, 58, 67]. Эффект состоит в возникновении на боковых гранях проводника с током (размерами: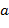 
– высота, 
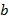– ширина и 
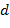– длина, где 
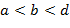– проводник должен быть достаточно объемным и представлять из себя пластину или брусок), помещенного в поперечное магнитное поле, разности потенциалов 
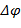(холловского напряжения 
, 
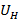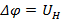) (рис. 1), пропорционального величине продольного тока 
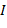и вектору индукции магнитного поля 
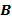[1, 54]. Эффект возникает вследствие воздействия силы Лоренца 
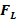на заряды в этом проводнике [36].
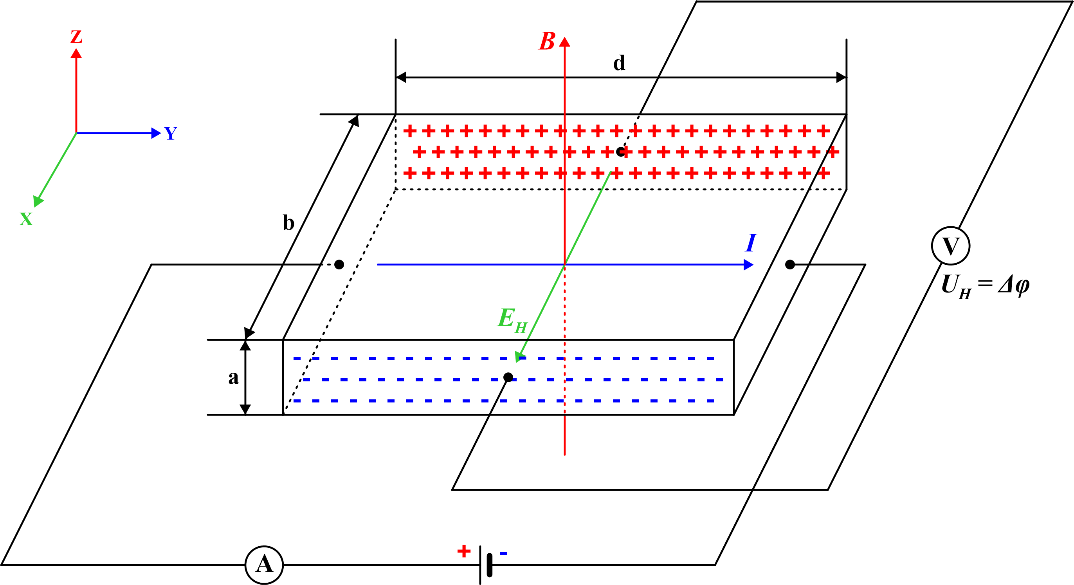
Рис. 1. Возникновение поперечной разности потенциалов 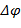в среде
Выражение для силы Лоренца имеет вид:
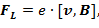(1)
где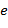 
– заряд электрона, 
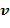– скорость движения электронов в проводнике.
Скапливающиеся на боковых краях холловского элемента заряды создают электрическое поле напряженностью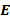 
, воздействующее на проводник с силой:
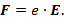(2)
Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, две эти силы – 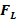и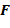 
, уравновешивают друг друга:
(3)
Из формулы плотности тока 
имеем скорость перемещения зарядов в проводнике :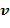
=> 
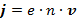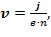(4)
где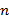 
– концентрация электронов (количество электронов на единицу объема).
Подставив это выражение в формулу (3), находим:
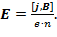(5)
Разность потенциалов 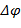между боковыми гранями проводника будет равна:
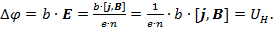(6)
Отсюда можно выразить постоянную Холла – холловское сопротивление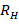 
, характеризующее материал, из которого изготовлен холловский элемент:
|
|
|
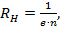(7)
Важно отметить, что знак постоянной Холла совпадает со знаком носителя заряда в веществе.
Теперь выражение (6) примет вид:
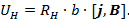(8)
Свой эксперимент Холл проводил на размещенной на стеклянной подложке золотой пластинке, при пропускании через которую магнитного потока возникала разность потенциалов на боковых краях пластины [67]. Некоторое время спустя этот эксперимент был повторен для пластин из других металлов и, всякий раз, получались аналогичные результаты.
В 1880 году результаты, полученные Эдвином Холлом, были опубликованы в качестве тезисов его докторской работы в журналах «American journal of mathematics» [67], «American journal of science» и «Philosophical magazine» [57, 58].
Далее развитие знаний об эффекте Холла как о физическом феномене нашло свое отражение в ряде базовых образовательных (например, [1, 36, 54, 57, 58]) и научных (например, [59-73, 76]) источниках, но применительно к геофизике целенаправленные исследования эффекта Холла автору данной работы на момент ее написания найти не удалось. В указанных выше источниках довольно подробно изложены механизм и физический смысл изучаемого эффекта, отражены исследования его проявления в самых различных средах и условиях, а также способы применения этих знаний в современных науке и технике.
Распространяя вышесказанное об эффекте Холла как о физическом феномене на условия геологической среды, можно заметить следующее:
1. В рассматриваемых масштабах проводящая геологическая среда является неограниченным проводником;
2. Согласно физической теории в ней также возникает поперечная э. д. с. в присутствии естественных или искусственных электрических токов, ведь стороннее магнитное поле есть всегда – это магнитное поле Земли.
В работе [28] описаны некоторые факты электроразведки ЗС, которые могут быть отнесены на счет влияния геомагнитного поля. Далее будет описан специальный эксперимент с целью регистрации эффекта Холла в геологической среде. Учитывая наличие силы Лоренца 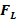, можно представить первое уравнение Максвелла в виде:
|
|
|
(9)
где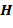 
– напряженность магнитного поля в геологической среде, 
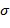– проводимость среды, 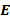– напряженность индуцируемого в электроразведке ЗС электрического поля, 
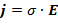– плотность возбуждаемых в среде токов, 
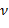– коэффициент (в м/А), удовлетворяющий размерности и учитывающий способность среды к появлению холловского (поперечного ) тока,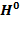 
– напряженность магнитного поля Земли. Выражение (9) можно представить иначе:
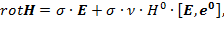(10)
здесь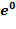 
– единичный вектор в направлении земного поля.
Видно, что дополнительная холловская проводимость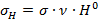 
складывается из разнородных факторов. Отчасти, она присуща среде и связана (посредством коэффициента 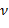) с такими характеристиками микропроцессов, как подвижность носителей тока, длина свободного пробега и прочее. Холловская проводимость 
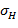также пропорциональна обычной проводимости 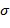и напряженности земного поля 
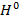. Есть еще один переменный фактор – конфигурация токов по отношению к направлению поля Земли. Эту ситуацию можно описать эффективной тензорной проводимостью (холловской анизотропией).
Рассмотрим наиболее простую ситуацию: процесс становления от горизонтальной токовой петли в горизонтально-слоистой среде – в таком случае решение известно (например, [8]). Примем, что магнитное поле Земли вертикально. Поле осесимметрично, и в цилиндрической системе координат имеет две магнитные компоненты 
, 
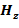и одну электрическую – 
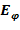[77]. Тогда из уравнения (10), раскрывая векторное произведение, появляется радиальная плотность тока:
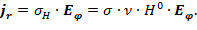(11)
В первом приближении 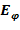есть решение задачи без учета магнитного поля Земли. Появление радиального тока 
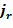возможно трактовать двояко: можно рассматривать эффективную тензорную проводимость с холловскими компонентами 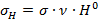или считать, что в изотропной среде с проводимостью 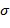появляется холловская радиальная электрическая компонента (рис. 2), перпендикулярная :
|
|
|
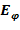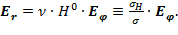(12)
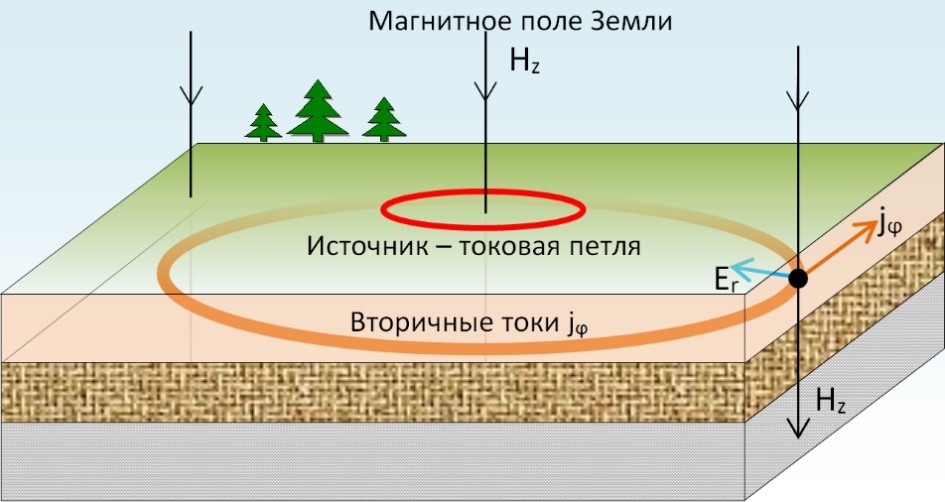
Рис. 2. Появление холловской (радиальной) компоненты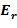 
электрического поля [29]
Первую трактовку удобно использовать в МТЗ, однако в ЗС эффективный тензор проводимости 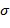станет зависимым от типа источника, что неудобно.
Зная параметр 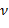, можно проводить прямое моделирование процессов становления с учетом геомагнитного фактора. Параметр 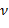можно связать с подвижностью носителей тока 
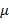и с коэффициентом Холла 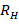, определенными для некоторых материалов и меняющимися в широких пределах. Проблема заключается в том, что это не имеет отношения к геологической среде. В этой работе, а также в [10-14, 26-34], предлагается способ экспериментального определения параметров эффекта Холла в геологической среде.
Как показывает формула (12), применяя токовую петлю и измеряя радиальной линией разность потенциалов:
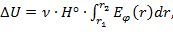(13)
где 
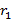и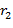 
– удаление, соответственно, ближнего и дальнего концов радиальной приемной линии от центра генераторной петли. Здесь для известной горизонтально-слоистой среды функция 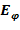, хорошо известна. Можно рассчитать коэффициент 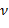, определяющий геомагнитный эффект в ЗС.
Таким образом, предлагается простая экспериментальная схема (рис. 3). На выбранном участке (удаленном от объектов, способных создать помехи для ЗС) с ровной поверхностью и горизонтально-слоистым разрезом (насколько это известно) располагается источник – токовая петля с импульсным возбуждением. Процесс становления регистрируется радиальной приемной линией при четырех одинаковых ее положениях относительно петли. В итоге мы имеем установку метода чистой аномалии в ЗС – этот факт требует проведения полевых экспериментов в особых условиях, которые будут описаны далее, но при этом позволяет добиться устранения влияния прямого поля ЗС – сигнала от геологической среды.
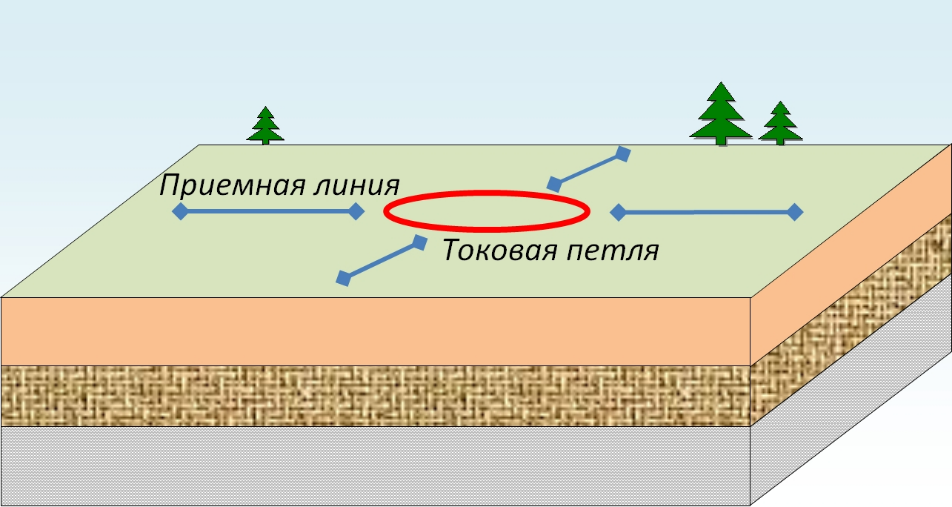
Рис. 3. Схема определения холловской (поперечной) проводимости в ЗС [29]
Генераторно-измерительная установка также должна быть большой, как для структурных исследований, чтобы максимально увеличить измеряемый сигнал от эффекта Холла. Желательно также перемещать (для исключения влияния среды и обстановки на конкретной территории) и поворачивать (для исследования сигналов в линиях, ориентированных, относительно сторон света, по разным направлениям) всю расстановку и повторять измерения (для проверки повторяемости результатов эксперимента).
|
|
|
Важным критерием, который поможет установить природу регистрируемых в ходе полевого эксперимента сигналов, является то, что искомые сигналы, связанные с магнитным полем Земли, во всех четырех радиальных измерительных линиях должны быть одинаковыми в силу осевой симметрии, в то время как все мыслимые нарушения условий дадут совершенно разные сигналы, что будет продемонстрировано в последующем.
|
|
|
