 |
Тема 4. Показатели вариации
|
|
|
|
Пример 21
Имеются данные о распределении рабочих по тарифным разрядам (таблица 21.1).
Таблица 21.1 – Распределение рабочих по тарифным разрядам
| Тарифный разряд | |||||
| Число рабочих |
Определить: а) дисперсию; б) среднее квадратическое отклонение; в) коэффициент вариации.
Решение
Дисперсия ( ), или средний квадрат отклонений для рядов распределения, исчисляется по формуле
), или средний квадрат отклонений для рядов распределения, исчисляется по формуле
 ,
,
т. е. является средней арифметической квадратов отклонений каждого значения признака от общей средней.
Корень квадратный из дисперсии называется средним квадратическим отклонением:
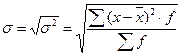 .
.
Выражается он в единицах измерения изучаемого признака.
Коэффициент вариации – относительный показатель колеблемости, равный процентному отношению среднего квадратического отклонения к средней арифметической:
 .
.
Как величина относительная, выраженная в процентах, коэффициент вариации применяется для сравнения степени вариации различных признаков.
Как видно из формул, для расчета показателей вариации необходимо предварительно определить среднюю величину. Исчислим указанные выше показатели вариации, представив необходимые расчеты в таблице 21.2.
Таблица 21.2 – Расчет показателей вариации
Тарифный разряд, 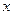
| Число рабочих, чел., 
| 
| 
| 
| 
|
| - 2,5 | - 2,5 | 6,25 | |||
| - 1,5 | - 3,0 | 4,50 | |||
| - 0,5 | 3,0 | 1,50 | |||
| 0,5 | 4,0 | 2,00 | |||
| 1,5 | 4,5 | 6,75 | |||
| Итого | - | - | 21,00 |
Определим показатели:
 разряда.
разряда.
 .
.
 разряда.
разряда.
 .
.
Так как  < 40%, то совокупность достаточно однародна и средняя характеристика достаточна надежна.
< 40%, то совокупность достаточно однародна и средняя характеристика достаточна надежна.
Пример 22
По данным условия предыдущего примера исчислить дисперсию по формуле
|
|
|
 .
.
Решение
Все расчеты представим в таблице 22.1.
Таблица 22.1 – Расчет дисперсии
Тарифный разряд, 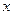
| Число рабочих, чел., 
| 
| 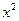
| 
|
| Итого | - |
Дисперсия равна

 .
.
Среднее квадратическое отклонение:
 разряда.
разряда.
Пример 23
Имеются данные о распределении работников организации обслуживания населения по размеру средней месячной заработной платы (таблица 23.1).
Таблица 23.1 – Распределение работников организации обслуживания населения по размеру средней месячной заработной платы
| Группы работников по размеру заработной платы, руб. | Численность работников, чел. |
| До 100 | |
| 100-120 | |
| 120-140 | |
| 140-160 | |
| 160-180 | |
| 180-200 | |
| Свыше 200 | |
| Итого |
Определить дисперсию заработной платы по способу моментов.
Решение
Способ моментов основан на математических свойствах дисперсии, применение которых значительно упрощает технику ее вычисления, а для рядов распределения с равными интервала приводит к формуле
 ,
,
где  – длина интервала;
– длина интервала;
 – момент первого порядка;
– момент первого порядка;
 – момент второго порядка;
– момент второго порядка;
 – ложный ноль.
– ложный ноль.
Определим дисперсию по формуле, представив необходимые расчеты в таблице 23.2.
Таблица 23.2 – Расчет дисперсии способом моментов
Группы работников по размеру заработной платы, руб., 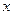
| Число работников, чел., 
| Середина интервала, 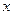
| 
| 
| 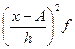
|
| До 100 | -3 | -6 | |||
| 100-120 | -2 | -24 | |||
| 120-140 | -1 | -15 | |||
| 140-160 | |||||
| 160-180 | |||||
| 180-200 | |||||
| Свыше 200 | |||||
| Итого | - | - |
Исчислим моменты первого и второго порядка:

 .
.
Затем вычислим средний квадрат отклонений (дисперсию):
 .
.
|
|
|
Пример 24
Удельный вес основных рабочих в трех цехах предприятия составил: 80, 75 и 90% общей численности рабочих. Определить дисперсию и среднее квадратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составила соответственно 100, 200 и 150 человек.
Решение
Рабочие предприятия подразделяются на две группы: основные и ремонтно-вспомогательные рабочие.
Общая численность основных рабочих по предприятию в целом составит:
 человек.
человек.
Доля основных рабочих по предприятию
 .
.
Дисперсия альтернативного признака составит
 ,
,
где  – доля единиц, обладающих данным признаком (доля основных рабочих);
– доля единиц, обладающих данным признаком (доля основных рабочих);
 – доля единиц, не обладающих данным признаком (доля ремонтно-вспомогательных рабочих).
– доля единиц, не обладающих данным признаком (доля ремонтно-вспомогательных рабочих).
Поскольку  , следовательно,
, следовательно, 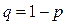 и формула дисперсии имеет вид
и формула дисперсии имеет вид
 .
.
Среднее квадратическое отклонение доли основных рабочих по предприятию в целом:
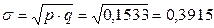 .
.
Пример 25
Для изучения взаимосвязи между стажем работы и производительностью труда (часовой выработкой) произведена группировка рабочих, приведенная в таблице 25.1.
Таблица 25.1 – Группировка рабочих по стажу работы с указанием среднечасовой выработки продукции на одного рабочего
| Группа, № | Группы рабочих по стажу, лет | Число рабочих, чел. | Среднечасовая выработка продукции одного рабочего, шт. |
| I | До 3 | 2; 2; 3; 3; 4 | |
| II | 3 – 5 | 2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 4; |
Определить:
1) среднюю часовую выработку продукции по каждой группе рабочих и по двум группам вместе;
2) дисперсию по каждой группе рабочих (групповые дисперсии) и среднюю из групповых дисперсий;
3) дисперсию групповых средних от общей средней (межгрупповую дисперсию);
4) общую дисперсию по правилу вложения дисперсий;
5) коэффициент детерминации;
6) эмпирическое корреляционное отношение.
Решение
1 Определим среднюю выработку по каждой группе рабочих и по двум группам:
 шт.;
шт.;  шт.;
шт.;
 шт. или
шт. или  шт.
шт.
2 Исчислим дисперсии по каждой группе рабочих по формуле:
 .
.
Предварительно строим по каждой группе рабочих ряды распределения по выработке (таблицы 25.2 и 25.3). Затем исчислим групповые дисперсии.
Таблица 25.2 – Ряд распределения первой группы рабочих по выработке
|
|
|
Выработка, шт., 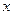
| Число
рабочих, чел., 
| 
| 
| 
|
| - 0,8 | 0,64 | 1,28 | ||
| 0,2 | 0,04 | 0,08 | ||
| 1,2 | 1,44 | 1,44 | ||
| Итого | - | - | 2,80 |
Дисперсия для первой группы  .
.
Таблица 25.3 – Ряд распределения второй группы рабочих по выработке
Выработка, шт., 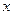
| Число
рабочих, чел., 
| 
| 
| 
|
| - 1,4 | 1,96 | 3,92 | ||
| - 0,4 | 0,16 | 0,80 | ||
| 0,6 | 0,36 | 2,88 | ||
| Итого | - | - | 7,60 |
Дисперсия для второй группы  .
.
Исчислим среднюю из групповых (частных) дисперсий по формуле
 ;
;
 .
.
3 Межгрупповая дисперсия
 ;
;
 .
.
4 Определим общую дисперсию по правилу сложения дисперсий
 ;
;
 .
.
5 Определяем коэффициент детерминации
 или 11,5%.
или 11,5%.
Коэффициент детерминации показывает, что вариация среднечасовой выработки рабочих обусловлена вариацией стажа лишь на 11,5%.
6 Исчислим эмпирическое корреляционное отношение
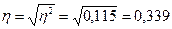 .
.
Оно показывает, что для данной группы рабочих связь между производственным стажем и среднечасовой выработкой незначительная.
Пример 26
Имеются данные о времени простоя автомобиля под разгрузкой (таблица 26.1).
Таблица 26.1 – Время простоя автомобиля под разгрузкой
| № пункта разгрузки | ||||||||||
| Число грузчиков | ||||||||||
| Время простоя, мин. |
Проверить закон сложения дисперсий.
Решение
В данной задаче варьирующим признаком является время простоя автомобиля под разгрузкой. Общая дисперсия времени простоя под разгрузкой определяется по формуле
 .
.
Для расчета общей дисперсии составляется дискретный ряд распределения, промежуточные расчеты представим в таблице 26.2.
Таблица 26.2 – Вспомогательная таблица для расчета общей дисперсии
Время простоя под разгрузкой, мин, 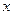
| Число выполненных разгрузок, 
| 
| 
| 
| 
|
| - 4 | |||||
| - 2 | |||||
| Итого | - | - |
 мин – среднее время простоя.
мин – среднее время простоя.
|
|
|
 – общая дисперсия.
– общая дисперсия.
Величина этой дисперсии характеризует вариацию времени простоя под разгрузкой под влиянием всех условий.
Различия в величине изучаемого признака прежде всего возникают под влиянием числа грузчиков, принимающих участие в процессе разгрузки. В связи с этим в совокупности выделяются две однородные группы по числу грузчиков: в первую группу включаются наблюдения при числе грузчиков 3; во вторую группу попадают наблюдения при числе грузчиков 4. Для каждой из выделенных групп определяется внутригрупповая дисперсия, возникающая под влиянием неучтенных факторов. Для их расчета использованы вспомогательные таблицы 26.3 и 26.4.
Таблица 26.3 – Расчет внутригрупповой дисперсии по первой группе (число грузчиков, участвующих в разгрузке, – 3)
Время простоя под разгрузкой, мин, 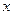
| Число
выполненных разгрузок, 
| 
| 
| 
|
| - 4 | ||||
| - 1 | ||||
| Итого | - |
 мин.;
мин.; 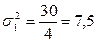 .
.
Таблица 26.4 – Расчет внутригрупповой дисперсии по второй группе (число грузчиков, участвующих в разгрузке, – 4)
Время простоя под разгрузкой, мин, 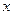
| Число
выполненных разгрузок, 
| 
| 
| 
|
| - 1,33 | 5,31 | |||
| 0,67 | 0,90 | |||
| 2,67 | 7,13 | |||
| Итого | - | 13,37 |
 мин.;
мин.;  .
.
Средняя из групповых дисперсий

Межгрупповая дисперсия, отражающая различия в величине признака под влиянием фактора, положенного в основу группировки, определяется по формуле

Общая дисперсия ( ) равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии
) равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии
 ,
,
что и соответствует полученной ранее величине.
Пример 27
Имеются данные о результатах обследования рабочих предприятия по размеру месячной заработной платы (таблица 27.1).
Таблица 27.1 – Информация о численности рабочих по возрасту и размере заработной платы
| Группы рабочих по возрасту, лет | Число рабочих | Дисперсия заработной платы |
| До 20 | ||
| 20-30 | ||
| 30 и старше |
Общая дисперсия заработной платы в обследованной совокупности рабочих составила 450.
Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста.
Решение
Средняя внутригрупповая дисперсия характеризует случайную вариацию под влиянием неучтенных факторов

Межгрупповая дисперсия отражает систематическую вариацию под влиянием фактора, положенного в основу группировки (возраста рабочих).
Межгрупповая дисперсия определяется по правилу сложения дисперсий

Отсюда соотношение дисперсий
 или 8,0%.
или 8,0%.
Полученный результат показывает, что возраст на варьирование заработной платы рабочих предприятия не оказывает существенного влияния.
|
|
|
Пример 28
Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найти среднюю величину.
Решение
Для нахождения средней величины воспользуемся формулой
 ,
,
где  – средняя арифметическая из квадратов индивидуальных значений признака;
– средняя арифметическая из квадратов индивидуальных значений признака;
 – квадрат среднего значения признака.
– квадрат среднего значения признака.
Тогда  .
.
Средняя величина признака
 .
.
Тема 5. Индексы
Пример 29
Имеются данные по одному из магазинов (таблица 29.1).
Таблица 29.1 – Объем реализации тканей по магазину
| Вид ткани | Реализовано, тыс. м | Цена за 1 м, ден. ед. | ||
базисный
период ( ) )
| отчетный
период (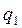 ) )
| базисный
период (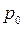 ) )
| отчетный
период (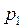 ) )
| |
| Хлопчатобумажные | 15,0 | 13,8 | 2,8 | 3,1 |
| Льняные | 9,5 | 10,0 | 6,0 | 7,8 |
Определить:
1 Индивидуальные индексы физического объема, цен.
2 Сводные индексы объема реализации, цен и товарооборота.
3 Абсолютное изменение товарооборота общее и в результате изменения цен и физического объема реализованных товаров.
Сделать выводы.
Решение
1 Рассчитаем индивидуальные индексы физического объема и цен.
Индивидуальный индекс физического объема ( ) равен
) равен
 .
.
 или 92%, т. е. объем реализации хлопчатобумажной ткани в отчетном периоде снизился по сравнению с базисным на 8% (92 – 100).
или 92%, т. е. объем реализации хлопчатобумажной ткани в отчетном периоде снизился по сравнению с базисным на 8% (92 – 100).
 или 105%, т. е. объем реализации льняной ткани в отчетном периоде увеличился по сравнению с базисным на 5% (105 – 100).
или 105%, т. е. объем реализации льняной ткани в отчетном периоде увеличился по сравнению с базисным на 5% (105 – 100).
Индивидуальный индекс цен ( ) объема равен
) объема равен
 .
.
 или 111%, т. е. цена за 1 метр хлопчатобумажной ткани увеличилась в отчетном периоде на 11% (111 – 100).
или 111%, т. е. цена за 1 метр хлопчатобумажной ткани увеличилась в отчетном периоде на 11% (111 – 100).
 или 130%, т. е. цена за 1 метр льняной ткани увеличилась в отчетном периоде на 30% (130 – 100).
или 130%, т. е. цена за 1 метр льняной ткани увеличилась в отчетном периоде на 30% (130 – 100).
2 Рассчитаем сводные индексы физического объема, цен и товарооборота.
Сводный индекс физического объема  равен
равен
 или 99,6%.
или 99,6%.
Сводный индекс цен  равен
равен
 или 122,4%.
или 122,4%.
Сводный индекс товарооборота  равен
равен
 или 122%
или 122%
или
 или 122%.
или 122%.
3 Абсолютное изменение товарооборота ( ) составит
) составит
 тыс. руб.
тыс. руб.
Абсолютное изменение товарооборота ( ) в результате изменения цен составит
) в результате изменения цен составит
 тыс. руб.
тыс. руб.
Абсолютное изменение товарооборота ( ) в результате изменения физического объема реализованных товаров составит
) в результате изменения физического объема реализованных товаров составит
 тыс. руб.
тыс. руб.



Следовательно, товарооборот в отчетном периоде по сравнению с базисным вырос на 22% или на 22,78 тыс. руб. Это произошло за счет влияния двух факторов:
- за счет роста цен товарооборот вырос на 22,4% или на 22,14 тыс. руб.;
- за счет изменения объема реализованных товаров товарооборот снизился на 0,4% или на 0,36 тыс. руб.
Пример 30
Имеются данные о продаже товаров в торговых предприятиях района (таблица 30.1).
Таблица 30.1 – Объем товарооборота торговых предприятий района
| Товар | Товарооборот, тыс. руб. | Изменение средних цен во II квартале по сравнению с I кварталом, % | |
| I квартал | II квартал | ||
| Обувь | +12 | ||
| Трикотаж | +5 | ||
| Изделия из кожи | +2 |
Определить:
1) изменение цен на проданные товары (индекс цен);
2) общий индекс товарооборота;
3) общий индекс физического товарооборота.
Решение
1 Общий индекс цен вычислим в форме среднего гармонического индекса
 ,
,
где  – индивидуальный индекс цен.
– индивидуальный индекс цен.
Определим индивидуальные индексы цен:
обувь 100 + 12 = 112%
трикотаж 100 + 5 = 105%
изделия из кожи 100 + 2 = 102%
Таким образом: 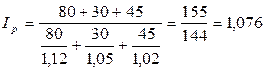 или 107,6%, т. е. цены в среднем выросли на 7,6%.
или 107,6%, т. е. цены в среднем выросли на 7,6%.
Сумма перерасхода, полученная населением от повышения цен, составит
155 – 144 = + 11 тыс. руб.
2 Общий индекс товарооборота составит
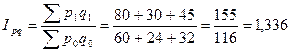 или 133,6%, т. е. товарооборот во II квартале вырос по сравнению с I кварталом на 33,6%, а в денежном выражении – на 39 тыс. руб. (155 – 116).
или 133,6%, т. е. товарооборот во II квартале вырос по сравнению с I кварталом на 33,6%, а в денежном выражении – на 39 тыс. руб. (155 – 116).
3 Общий индекс физического объема товарооборота составит
 или 124,1%, т. е. количество проданных товаров выросло на 24,1%, что составляет 28 тыс. руб.
или 124,1%, т. е. количество проданных товаров выросло на 24,1%, что составляет 28 тыс. руб.
Между вычисленными индексами существует взаимосвязь:

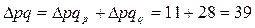 тыс. руб.
тыс. руб.
Пример 31
Имеются данные по одной из кондитерских фабрик (таблица 31.1).
Таблица 31.1 – Затраты на производство продукции кондитерской фабрики
| Вид продукции | Общие затраты на производство продукции, тыс. ден. ед. | Индивидуальный индекс физического объема продукции | |
| базисный период | отчетный период | ||
| Карамель | 25,0 | 27,0 | 1,05 |
| Шоколадные конфеты | 54,0 | 55,0 | 1,12 |
Определить абсолютное изменение затрат на производство продукции за счет изменения физического объема и себестоимости произведенной продукции.
Решение
Абсолютное изменение затрат на производство за счет изменения физического объема продукции ( ) найдем как разницу между числителем и знаменателем индекса физического объема
) найдем как разницу между числителем и знаменателем индекса физического объема
 .
.
Из формулы  выразим
выразим  , тогда
, тогда
 или 109,8%,
или 109,8%,
 тыс. ден. ед.
тыс. ден. ед.
Абсолютное изменение затрат на производство за счет изменения себестоимости ( ) найдем как разницу между числителем и знаменателем сводного индекса себестоимости
) найдем как разницу между числителем и знаменателем сводного индекса себестоимости
 или 94,5%,
или 94,5%,
 тыс. ден. ед.
тыс. ден. ед.
Следовательно, за счет роста объема произведенной продукции на 9,8% затраты на производство продукции выросли на 7,73 тыс. ден. ед., однако снижение цен на 5,5% способствовало снижению затрат на 4,73 тыс. ден. ед.
Пример 32
Имеются данные о производстве продукции и затратах времени на ее производство (таблица 32.1).
Таблица 32.1 – Объем производства продукции за базисный и отчетный год и затраты времени на ее производство
| Вид продукции | Базисный год | Отчетный год | ||
произведено, тыс. ц
( ) )
| затрачено
тыс. чел./дн. ( ) )
| произведено, тыс. ц
( ) )
| затрачено
тыс. чел./дн. ( ) )
| |
| Лук | 7,3 | 7,5 | ||
| Морковь | 7,6 | 7,7 |
Определить индекс производительности труда.
Решение
Индекс производительности труда рассчитывается по формуле
 ,
,
где  – индекс трудоемкости;
– индекс трудоемкости;
 ,
,  – трудоемкость соответственно в базисном и отчетном году.
– трудоемкость соответственно в базисном и отчетном году.
Трудоемкость рассчитывается по формуле
 ,
,
где  – затраты рабочего времени;
– затраты рабочего времени;
 – объем производства продукции.
– объем производства продукции.
Трудоемкость за отчетный период равна
 чел.-дн./ц;
чел.-дн./ц;  чел.-дн./ц.
чел.-дн./ц.
Трудоемкость за базисный период равна
 чел.-дн./ц;
чел.-дн./ц;  чел.-дн./ц.
чел.-дн./ц.
Таким образом
 или 104,4%, т. е. производительность труда в отчетном периоде по сравнению с базисным увеличилась на 4,4%.
или 104,4%, т. е. производительность труда в отчетном периоде по сравнению с базисным увеличилась на 4,4%.
Пример 33
Динамика себестоимости и объема продукции характеризуется данными, представленными в таблице 33.1.
Таблица 33.1 – Объем произведенной продукции по заводам за базисный и отчетный периоды
| Завод | Выработано продукции, тыс. ед. | Себестоимость единицы продукции, тыс. руб. | ||
базисный
период
( ) )
| отчетный
период
( ) )
| базисный
период
( ) )
| отчетный
период
( ) )
| |
| Завод №1 | 7,0 | 7,4 | ||
| Завод №2 | 6,8 | 7,0 |
Определить:
1) индекс себестоимости переменного состава;
2) индекс себестоимости постоянного состава;
3) индекс изменения структуры.
Решение
1 Индекс себестоимости переменного состава (индекс среднего уровня) рассчитывается по формуле
 .
.
Индекс показывает, как изменилось среднее значение показателя за счет двух факторов (изменения самой себестоимости на отдельном заводе и изменений в структуре выработанной продукции).
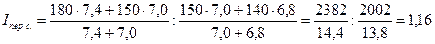 или 116%.
или 116%.
2 Индекс себестоимости постоянного (фиксированного) состава рассчитывается по формуле
 .
.
Индекс показывает, как изменилось среднее значение показателя за счет изменения первого фактора (себестоимости).
 или 114%.
или 114%.
3 Индекс структурных сдвигов рассчитывается по формуле
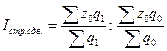 .
.
Индекс показывает, как изменилось среднее значение показателя за счет изменения второго фактора (объема произведенной продукции).
 или 102%.
или 102%.
Между этими индексами существует связь:

Следовательно, среднее значение себестоимости по двум заводам в отчетном периоде по сравнению с базисным увеличилось на 16%. За счет изменения себестоимости единицы продукции по отдельным заводам среднее значение себестоимости по двум заводам увеличилось на 14%. За счет изменений в структуре объема выработанной продукции среднее значение себестоимости увеличилось на 2%.
Пример 34
Расходы консолидированного бюджета Республики Беларусь на социально-культурные мероприятия представлены в таблице 34.1.
Таблица 34.1 – Расходы консолидированного бюджета Республики Беларусь на социально-культурные мероприятия
| Виды расходов | Фактически действовавшая цена, млрд руб. | Объем расходов, млн руб. | ||
| город А | город Б | город А | город Б | |
| Здравоохранение | 32,5 | 17,8 | ||
| Образование | 44,6 | 24,1 | ||
| Физическая культура, спорт, культура и СМИ | 7,6 | 4,6 |
Рассчитать территориальный индекс цен на эти виды расходов в городе А по сравнению с городом Б.
Решение
Территориальный индекс цен, в котором в качестве базы сравнений принимаются данные по городу А ( ), будет иметь вид
), будет иметь вид
 ,
,
где  ,
,  – фактически действующие цены в городе А и Б;
– фактически действующие цены в городе А и Б;
 – количество расходов в городе А и Б.
– количество расходов в городе А и Б.
Суммируем объем расходов в разных городах по каждому виду:
 ;
;
 ;
;
 .
.
Рассчитаем территориальный индекс цен:
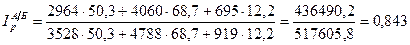 или 84,3%.
или 84,3%.
Таким образом, цены на расходы в городе А ниже на 15,7% по сравнению с ценами в городе Б.
|
|
|


