Тема 6. Статистическое изучение динамики

 

Пример 35

Имеются данные о количестве безработных за 2007 год (таблица 35.1).

 

Таблица 35.1 – Количество безработных в Республике Беларусь за 2007 год

Период	Январь	Февраль	Март	II квартал
Количество безработных, тыс. чел.

 

Определить среднемесячное количество безработных за I квартал и за первое полугодие.

 

Решение

По условию примера дан интервальный ряд с равными интервалами. Таким образом, среднемесячное количество безработных найдем по формуле:

.

где − уровень (значение) ряда;

– количество периодов.

 

За I квартал среднемесячное количество безработных составит

тыс. чел.

За первое полугодие среднемесячное количество безработных составит

тыс. чел.

 

 

Пример 36

Остатки вкладов в сберегательной кассе на 1-е число месяца составили:

январь – 450 тыс. руб.;

апрель – 485 тыс. руб.;

июль – 462 тыс. руб.;

октябрь – 443 тыс. руб.;

январь следующего года – 470 тыс. руб.

Определить средний годовой остаток вкладов в сберегательной кассе.

 

Решение

Средний годовой остаток вкладов определим по средней хронологической для моментных рядов с равными интервалами, т. к. промежутки времени между датами равны и составляют 3 месяца:

тыс. руб.

 

 

Пример 37

Остатки вкладов в сберегательной кассе на 1-е число месяца составили:

январь – 460 тыс. руб.;

май – 475 тыс. руб.;

август – 469 тыс. руб.;

октябрь – 484 тыс. руб.;

январь следующего года – 490 тыс. руб.

Определить средний годовой остаток вкладов в сберегательной кассе.

 

Решение

Так как данные приведены на 1-е число месяца и промежутки времени между датами не равны, для расчета среднего годового остатка вкладов в сберегательной кассе будем использовать среднюю хронологическую для моментных рядов с неравными интервалами

,

где – средний уровень в интервалах между датами,

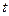– период времени.

Таким образом, средний годовой остаток вкладов в сберегательной кассе составит:

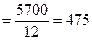тыс. руб.

 

 

Пример 38

Номинальная заработная плата работников народного хозяйства Республики Беларусь характеризуется данными, представленными в таблице 38.1.

 

Таблица 38.1 – Номинальная заработная плата работников народного хозяйства Республике Беларусь

Год
Размер заработной платы, тыс. руб.	58,9	123,0	189,2	250,7	347,5	463,7	582,2	701,1

 

Для анализа динамики заработной платы определить:

1) среднегодовой размер заработной платы за 8 лет;

2) ежегодные и базисные абсолютные приросты, темпы роста и прироста заработной платы;

3) абсолютное значение 1% прироста;

4) среднегодовой абсолютный прирост;

5) среднегодовой темп роста и среднегодовой темп прироста;

6) среднее значение 1% прироста.

Результаты представить в таблице, сделать выводы.

 

Решение

1 Среднегодовой размер заработной платы определим по формуле средней арифметической простой

тыс. руб.

 

2 Ежегодный (цепной) абсолютный прирост (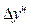) определим по формуле

,

где , – значение показателя соответственно в -м периоде и предшествующем ему.

Например, для 2001 года тыс. руб., т. е. заработная плата в 2001 году по сравнению с 2000 годом выросла на 64,1 тыс. руб.; для 2002 года 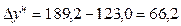тыс. руб. и т. д.

Базисный абсолютный прирост () определим по формуле

,

где , 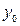– значение показателя соответственно в -м и базисном (2000 год) периоде.

Например, для 2001 года тыс. руб.; для 2002 года тыс. руб., т. е. заработная плата в 2002 году по сравнению с 2000 годом увеличилась на 130,3 тыс. руб. и т. д.

 

Цепной темп роста определим по формуле

.

Например, для 2001 года , т. е. заработная плата в 2001 году по сравнению с 2000 годом выросла на 108,8%; для 2002 года и т. д.

 

Базисный темп роста определим по формуле

.

Например, для 2001 года 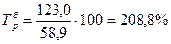; для 2002 года , т. е. заработная плата в 2002 году по сравнению с 2000 годом выросла на 221,2% и т. д.

 

Темп прироста найдем по формуле

.

Так, цепной темп прироста

за 2001 год: ;

за 2002 год: .

Базисный темп прироста

за 2001 год: ;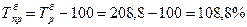

за 2002 год: .

 

3 Абсолютное значение 1% прироста () найдем по формуле

.

Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:

.

Например, для 2001 года тыс. руб.; для 2002 года тыс. руб.

 

Расчеты показателей по пунктам 1, 2, 3 оформим в таблице 38.2.

 

Таблица 38.2 – Показатели динамики заработной платы за 2000-2007 гг.

Год	Размер заработной платы, тыс. руб.	Абсолютный прирост, тыс. руб.	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста, тыс. руб.
цепной	базисный	цепной	базисный	цепной	базисный
	58,9	-		-		-		-
	123,0	64,1	64,1	208,8	208,8	108,8	108,8	0,589
	189,2	66,2	130,3	153,8	321,2	53,8	221,2	1,23
	250,7	61,5	191,8	132,5	425,6	32,5	325,6	1,892
	347,5	96,8	288,6	138,6		38,6		2,507
	463,7	116,2	404,8	133,4	787,3	33,4	687,3	3,475
	582,2	118,5	523,3	125,6	988,5	25,6	888,5	4,637
	701,1	118,9	642,2	120,4	1190,3	20,4	1090,3	5,822

 

4 Среднегодовой абсолютный прирост вычисляется двумя способами:

1) как средняя арифметическая простая годовых (цепных) приростов, т.е.:

;

2) как частное от деления базисного прироста к числу периодов

.

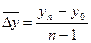Так тыс. руб.

или тыс. руб.

5 Среднегодовой темп роста найдем по формуле

,

где – число темпов роста цепных;

или

,

где – число периодов.

 

Так или 143%.

Либо или 143%.

Среднегодовой темп роста заработной платы за 2000-2007 гг. составляет 143%, следовательно, среднегодовой прирост составит 43%.

 

6 Среднее значение 1% прироста рассчитаем по формуле

.

Так тыс. руб.

 

Таким образом, на протяжении 2000-2007 гг. наблюдается положительная динамика роста заработной платы. Так, среднегодовой абсолютный прирост составил 91,7 тыс. руб. или 43%.

 

 

Пример 39

Имеются данные о реализации овощей по Минской области за три года (таблица 39.1).

 

 

Таблица 39.1 – Объем реализованных овощей по Минской области за 2005-2007 гг. (тыс. т)

Год

Месяц

 

Определить индексы сезонности. Построить сезонную волну.

 

Решение

Индекс сезонности определим по формуле

,

где – одноименные (одномесячные) средние (в нашем примере в среднем за три года);

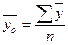– общая средняя;

– средний уровень ряда за год.

Например, в январе ;

в феврале и т. д.

Средний уровень ряда равен

2005 год ;

2006 год ;

2007 год .

Общая средняя равна

тыс. т.

Таким образом, индекс сезонности будет равен

в январе ;

в феврале ;

и т. д. по месяцам. Расчеты представим в таблице 39.2.

 

Таблица 39.2 – Расчет индексов сезонности

Месяц	Реализация овощей по Минской области, тыс. т	Индекс сезонности, %
2005 год	2006 год	2007 год	в среднем за три года
Январь
Февраль				8,7	23,5
Март				12,7	34,2
Апрель				18,7	50,4
Май				23,7	63,9
Июнь				37,7	101,6
Июль				38,7	104,3
Август					94,3
Сентябрь				84,7	228,3
Октябрь				92,7
Ноябрь				42,7
Декабрь				40,7	109,7
Средний уровень ряда ()	35,9		36,3	37,1

 

Изобразим на графике сезонную волну:

 

По результатам вычислений следует, что на осень приходится самый большой объем реализации овощей.

 

 

Пример 40

Имеются данные о производстве тракторов за четыре года (таблица 40.1).

 

Таблица 40.1 – Информация о производстве тракторов за 2003-2006 гг.

Год	Производство тракторов, тыс. шт.
	22,5
	22,7
	24,3
	26,7

 

Определить тенденцию производства тракторов за изученный период и сделать прогноз на 2009 год.

 

Решение

Для того, чтобы определить тенденцию производства и сделать прогноз, проведем аналитическое выравнивание ряда динамики по прямой.

Уравнение прямой имеет вид

,

где , 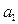– параметры уравнения;

– время.

 

Для нахождения параметров и 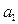решим систему уравнений

или воспользуемся готовыми формулами

и .

Поскольку время, перейдем к условным годам, выбрав начало отсчета таким образом, чтобы .

Расчеты приведем в таблице 40.2.

 

Таблица 40.2 – Расчет параметров уравнения

Год	Производство тракторов, тыс. шт. ()
	22,5	- 3		- 67,5
	22,7	- 1		- 22,7
	24,3			24,3
	26,7			80,1
Всего	96,2			14,2

 

тыс. шт. и тыс. шт.

Таким образом, уравнение прямой имеет вид

,

т. е. средний годовой объем производства равен 24,05 тыс. шт., ежегодный прирост составляет 0,71 тыс. шт.

Прогноз на 2009 год найдем подставив в уравнение период времени, т. е.

тыс. шт.

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: