 |
Тема 8. Статистическое изучение взаимосвязи
|
|
|
|
Пример 48
Имеются данные о распределении предприятий по дневной заработной плате и уровню организации (таблица 48.1).
Таблица 48.1 – Распределение предприятий по дневной заработной плате и уровню организации
| Уровень организации Дневная зарплата | Ниже среднего | Средний | Выше среднего | Всего |
| Ниже среднего | 2,77 (36) | 2,45 (49) | 4,77 (81) | 9,99 0,45 |
| Средняя | 0,69 (9) | 3,2 (64) | 0,24 (4) | 4,13 0,32 |
| Выше среднего | 1,23 (16) | 1,25 (25) | 2,12 (36) | 4,6 0,31 |
| Итого | 1,08 |
Необходимо оценить тесноту связи между уровнем организации и дневной заработной платой с помощью коэффициентов взаимной сопряженности Пирсона и Чупрова.
Решение
1 Возведем каждую частоту в квадрат и результат запишем в этой же клетке, только в скобках.
2 Делим каждое число, стоящее в скобках на число стоящее в итоговой строке соответствующего столбца и записываем в этой же клетке (например, 
).
3 Полученные числа складываем по строкам и результат записываем в графе «Всего» (например, 
).
4 В графе «Всего» в каждой клетке второе число делим на первое (например,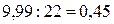 
).
5 Полученные числа складываем и результат записываем в правом нижнем углу таблицы (
).
6 Для исследования тесноты связи между признаками, рассчитаем коэффициенты Пирсона и Чупрова
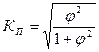и 
,
где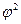 
– показатель взаимной сопряженности;
– количество групп по первому признаку;
– количество групп по второму признаку.
Коэффициент Чупрова всегда меньше коэффициента Пирсона. Он дает обычно более осторожную оценку связи. Коэффициенты принимают значения от 0 до 1, и чем ближе к 1, тем теснее связь.
Показатель взаимной сопряженности
.
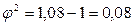Рассчитаем коэффициент Пирсона
|
|
|
.
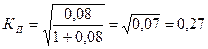Рассчитаем коэффициент Чупрова
.
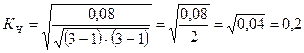Так как коэффициенты Пирсона и Чупрова значительно ниже 1, то связь между признаками незначительна.
Пример 49
В результате обследования работников предприятия получены следующие данные (таблица 49.1).
Таблица 49.1 – Сведения об уровне образования и степени удовлетворенности работников своей работой
| Образование | Удовлетворены своей работой | Не удовлетворены своей работой | Итого |
| Высшее и среднее | |||
| Незаконченное среднее | |||
| Итого |
Требуется оценить тесноту связи между уровнем образования работников и удовлетворенностью своей работой с помощью коэффициентов ассоциации и контингенции.
Решение
Коэффициенты ассоциации и контингенции применяются тогда, когда исследуется связь между варьированием двух атрибутивных (пол, национальность, профессия) признаков, по каждому признаку имеется две группы (таблица 49.2).
Таблица 49.2 – Варьируемые атрибутивные признаки
| Всего | |||
| a | b | a+b | |
| c | d | c+d | |
| Итого | a+c | b+d | a+b+c+d |
Коэффициент ассоциации
.
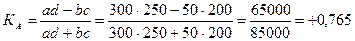Коэффициент контингенции
.
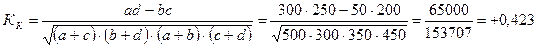Коэффициенты контингенции и ассоциации принимают значение от -1 до 1, показывают не только тесноту, но и направление связи.
Если коэффициент >0, связь прямая, <0 – обратная. Чем ближе коэффициент к ±1, тем связь теснее.
Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками. Однако коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.
Пример 50
Урожайность плодов и ягод по Могилевской области за 2007 год характеризуется данными, представленными в таблице 50.1.
Таблица 50.1 – Показатели урожайности плодов и ягод по колхозам Могилевской области за 2007 год
| Номер колхоза | Урожайность, ц/га ( )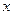
| Внесено
удобрений
на 1 га ( )
| Знаки отклонений | |
| 
| |||
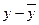
| 31,9 | 15,5 | - | - | |
| 33,3 | 11,3 | - | - | |
| 32,9 | 39,7 | - | + | |
| 34,4 | 15,7 | - | - | |
| 52,3 | 61,4 | + | + | |
| 26,4 | 14,6 | - | - | |
| 39,4 | 47,4 | - | + | |
| 41,6 | 50,1 | + | + | |
| 77,3 | 80,5 | + | + | |
| 45,9 | 45,1 | + | + | |
| Итого | 415,4 | 381,3 |
Определите тесноту связи с помощью коэффициентов знака Фехнера между урожайностью плодов и ягод по колхозам Могилевской области и количеством внесенных удобрений.
|
|
|
Решение
Коэффициент Фехнера основан на методе параллельных рядов. Суть его в том, что сравниваются знаки отклонений значений признака от их средних арифметических.
Найдем средние арифметические по формуле
; 
.
; 
.
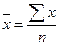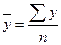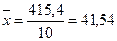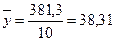Рассмотрим совпадение и несовпадение знаков отклонений.
Совпадение знаков (С) означает согласованную вариацию, а несовпадение (Н) – нарушение этой согласованности.
С = 8; Н = 2.
Коэффициент Фехнера вычисляется по формуле
.
Принимает значения от –1 до +1. Знак «–» означает, что связь обратная, «+» − связь прямая. Чем ближе коэффициент к ±1, тем связь теснее.
Вычислим коэффициент Фехнера:
.
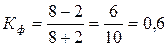Следовательно, связь прямая и заметно согласованная.
Пример 51
По группе акционерных коммерческих банков региона имеются данные о сумме прибыли банков и размере активов (таблица 51.1).
Таблица 51.1 – Информация о размере прибыли коммерческих банков и стоимости активов
| № банка | Активы банка, млн руб. | Прибыль банка, млн руб. |
| 39,6 | ||
| 17,8 | ||
| 12,7 | ||
| 14,9 | ||
| 4,0 | ||
| 15,5 | ||
| 6,4 | ||
| 10,1 | ||
| 3,4 | ||
| 13,4 |
Исчислить коэффициент корреляции рангов для оценки тесноты связи между суммой прибыли банка и размером его активов.
Решение
Для расчета коэффициента корреляции рангов предварительно выполняется ранжирование банков по уровню каждого признака (таблица 51.2).
Таблица 51.2 – Ранжирование банков
| № банка | Активы банка, млн руб. ()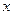
| Ранг
по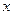
| № банка | Прибыль банка, млн руб. ()
| Ранг
по
|
| 3,4 | |||||
| 4,0 | |||||
| 6,4 | |||||
| 10,1 | |||||
| 12,7 | |||||
| 13,4 | |||||
| 14,9 | |||||
| 15,5 | |||||
| 17,8 | |||||
| 39,6 |
|
|
|
Коэффициент корреляции рангов найдем по формуле
,
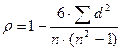где 
– разность рангов;
– число единиц совокупности.
Дальнейшие расчеты произведем в таблице 51.3.
Таблица 51.3 – Вспомогательная таблица для расчета коэффициента корреляции рангов
| Активы банка,
млн руб. ()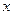
| Прибыль банка, млн руб. ()
| Ранги | 
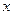(ранг – ранг )
| 
| ||
|
|
| |||||
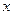
| 39,6 | ||||||
| 17,8 | - 1 | |||||
| 12,7 | ||||||
| 14,9 | - 2 | |||||
| 4,0 | ||||||
| 15,5 | - 6 | |||||
| 6,4 | ||||||
| 10,1 | ||||||
| 3,4 | ||||||
| 13,4 | ||||||
| Итого |
Следовательно, связь между признаками прямая и заметная.
Пример 52
По группе предприятий имеются данные о стоимости суммарных активов и сумме чистой прибыли (таблица 52.1).
Таблица 52.1 – Информация о стоимости суммарных активов предприятий и размере их чистой прибыли
| № предприятия | Суммарные активы, млн руб. | Чистая прибыль, тыс. руб. |
| 4 613 | ||
| 5 929 | ||
| 1 705 | ||
| 4 591 | ||
| 6 321 | ||
| 1 778 | ||
| 2 186 | ||
| 6 768 | ||
| 4 362 | ||
| 7 129 | ||
| 5 227 | ||
| 4 355 |
На основании приведенных данных
1) оценить тесноту связи между результативным и факторным признаком с проверкой коэффициента корреляции на значимость;
2) построить линейное уравнение парной регрессии между чистой прибылью и суммарными активами, оценить на основании расчета различных коэффициентов полученные результаты.
Решение
1 Необходимые данные вычислим в таблице 52.2.
Таблица 52.2 – Вспомогательная таблица
| № предприятия | Суммарные активы,
млн руб.
()
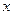| Чистая
прибыль,
тыс. руб.
()
| 
| 
| 
|
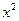
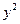
| 4 613 | 1 591 485 | 21 279 769 | 119 025 | ||
| 5 929 | 2 976 358 | 35 153 041 | 252 004 | ||
| 1 705 | 209 715 | 2 907 025 | 15 129 | ||
| 4 591 | 1 657 351 | 21 077 281 | 130 321 | ||
| 6 321 | 2 945 586 | 39 955 041 | 217 156 | ||
| 56 140 | 643 204 | 4 900 | |||
| 1 778 | 234 696 | 3 161 284 | 17 424 | ||
| 62 613 | 597 529 | 6 561 | |||
| 2 186 | 404 410 | 4 778 596 | 34 225 | ||
| 6 768 | 3 329 856 | 45 805 824 | 242 064 | ||
| 4 362 | 1 605 216 | 19 027 044 | 135 424 | ||
| 7 129 | 3 393 404 | 50 822 641 | 226 576 | ||
| 62 152 | 835 396 | 4 624 | |||
| 5 227 | 2 017 622 | 27 321 529 | 148 996 | ||
| 4 355 | 1 641 835 | 18 966 025 | 142 129 | ||
| Итого | 57 453 | 4 432 | 22 188 439 | 292 331 229 | 1 696 558 |
|
|
|
Оценка тесноты связи определяется с помощью коэффициента корреляции
;
; 
.
; 
.
; 
.
.
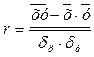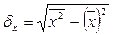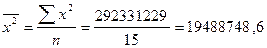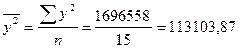Так как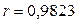 
, то связь прямая, сильная.
2 Линейное уравнение парной регрессии имеет вид
.
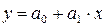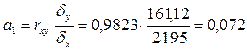, т. е. при увеличении стоимости суммарных активов на 1 млн руб. чистая прибыль в среднем увеличивается на 0,072 тыс. руб.
.
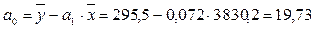Таким образом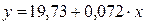 
Коэффициент детерминации 
или 96,49%, т. е. вариация результативного признака на 96,49% обусловлена различиями факторного признака и на 3,51% (100 – 96,49) – другими факторами.
Коэффициент эластичности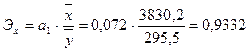 
, т. е. при увеличении стоимости суммарных активов на 1% чистая прибыль в среднем увеличится на 0,9332%.
Учебное издание
СТАТИСТИКА
Часть I
Теория статистики
Методические указания
Составители: Малышева Ольга Дмитриевна
Барсукова Ольга Григорьевна
Шкинёва Ольга Константиновна
Редактор А.А. Щербакова
Технический редактор М.О. Хлыстова
Подписано в печать Формат 60  84 1/16.
|
| Бумага офсетная. Гарнитура Таймс. Ризография. |
| Усл. печ. л. Уч.-изд. л. |
| Тираж экз. Заказ |
Отпечатано на ризографе редакционно-издательского отдела
учреждения образования
«Могилевский государственный университет продовольствия»
212027, Могилев, пр-т Шмидта, 3.
ЛИ № 02330/0131913 от 08.02.2007.
Рецензия
на методические указания к решению задач
по дисциплине «Статистика» часть I «Теория статистики»
для студентов экономических специальностей
1 – 25 01 08 «Бухгалтерский учет, анализ и аудит»
разработанные старшим преподавателем кафедры БУА и А Малышевой О.Д.,
ассистентом кафедры БУА и А Барсуковой О.Г.,
ассистентом кафедры БУА и А Шкинёвой О.К.
Методические указания к решению задач по дисциплине «Статистика» составлены в соответствии с программой курса «Статистика» для экономических специальностей и содержат указания и подробные решения задач по всем разделам курса.
Данные методические указания позволят студентам самостоятельно изучить дисциплину и приобрести практические навыки по решению задач.
Главная цель методических указаний – помочь студентам заочникам самостоятельно закрепить полученные теоретические навыки при выполнении контрольной работы.
Рецензируемая методическая разработка выполнена в соответствии с планом издания учебно-методической литературы кафедры бухгалтерского учета, анализа и аудита, является своевременной и актуальной.
|
|
|
Методические указания к решению задач по дисциплине «Статистика» часть I «Теория статистики» для студентов экономических специальностей отвечают современным требованиям экономической науки, написаны доступно и на высоком методическом уровне, поэтому они могут быть рекомендованы к изданию на ризографе УО МГУП и использованию в учебном процессе.
Рецензент: к.э.н., доцент Т.И. Сушко
|
|
|
