 |
Тема 7. Выборочное наблюдение
|
|
|
|
Пример 41
При проверке веса поставляемого груза методом случайной повторной выборки было отобрано 350 изделий. В результате был установлен средний вес изделия – 120 г при среднем квадратическом отклонении 9 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.
Решение
1 Рассчитаем предельную ошибку выборки (
) по формуле
,
где 
– коэффициент доверия, который зависит от вероятности, с которой можно гарантировать, что предельная ошибка выборки не превысит t -кратную среднюю ошибку (
при вероятности 0,997);
– средняя ошибка выборки.
Среднюю ошибку выборки рассчитаем по формуле
,
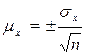где 
– среднее квадратическое отклонение;
– объем выборочной совокупности.
Таким образом
2 Определим пределы генеральной средней
,
где 
– среднее значение признака в генеральной совокупности;
– среднее значение признака в выборочной совокупности.
Для нашего примера
Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 118,557 г до 121,443 г.
Пример 42
В городе проживают 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей (таблица 42.1).
Таблица 42.1 – Состав семей по количеству детей
| Число детей в семье | ||||||
| Количество семей |
С вероятностью 0,954 найти пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение
|
|
|
На основании имеющегося распределения семей определим выборочную среднюю и дисперсию
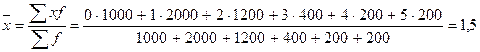чел.
Предельную ошибку выборки определим по формуле
,
где – коэффициент доверия, который зависит от вероятности, с которой можно гарантировать, что предельная ошибка выборки не превысит t -кратную среднюю ошибку (
при вероятности 0,954);
– средняя ошибка выборки.
Среднюю ошибку выборки для бесповторного отбора определим по формуле
,
где 
– дисперсия;
– объем выборочной совокупности;
– объем генеральной совокупности;
– доля выборки.
Таким образом
Определим пределы генеральной средней
Следовательно, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т. е. в среднем на каждые две семьи приходится 3 ребенка.
Пример 43
Произведено выборочное наблюдение партии однородной продукции для определения процента изделий высшего сорта. При механическом способе отбора из партии готовых изделий в 20 000 единиц было обследовано 800 единиц, из которых 640 изделий отнесены к высшему сорту.
Определить с вероятностью 0,997 возможный процент изделий высшего сорта во всей партии.
Решение
В случае механического отбора предельная ошибка выборки определяется по формуле
,
где – коэффициент доверия ( при вероятности 0,997);
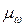– средняя ошибка выборки.
Средняя ошибка выборки равна
,
где 
– выборочная доля;
Таким образом
Определим пределы генеральной доли (
)
,
Следовательно, с вероятностью 0,997 можно утверждать, что доля изделий высшего сорта во всей партии находится в пределах от 76 до 84%.
Пример 44
В выборке объемом 1000 единиц доля бракованных изделий составила 3%. Выборка случайная, бесповторная. Необходимо определить вероятность того, что во всей партии изделий (10 000 штук) доля бракованных изделий находится в пределах от 2,5 до 3,5%.
|
|
|
Решение
Предельная ошибка выборки равна
.
Рассчитаем среднюю ошибку
.
Коэффициент доверия равен
.
Вероятность, соответствующую данной величине коэффициента, находим по таблицам интегральной функции Лапласа. Она будет равна 0,683.
Пример 45
По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин при среднем квадратическом отклонении 2 мин.
Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 с?
Решение
По условию задачи известны:
объем выборки –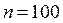 
;
выборочная средняя – 
мин;
выборочное среднее квадратическое отклонение – 
мин;
предельная ошибка выборки – 
сек.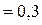 
мин;
; 
мин;
.
Затем по таблице интегральной функции Лапласа на основе значения определяется вероятность того, что ошибка не превысит заданной величины.
При 
вероятность 
.
Пример 46
На основании выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.
Требуется определить численность выборки, если результаты выборки дать с точность до 1% и гарантировать это с вероятностью 0,95.
Решение
По условию задачи известны:
размер допустимой (предельной) ошибки – 
или 0,01;
принятая вероятность – 
;
по таблице интегральной функции Лапласа при 
.
Необходимая численность выборки
.
Так как значение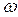 
не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение 
.
.
Таким образом, чтобы с заданной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.
Пример 47
Определить, сколько электроламп из всей партии изделий следует подвергнуть обследованию в порядке случайной бесповторной выборки, чтобы с вероятностью 0,954 предельная ошибка не превышала 3% среднего веса спирали (средний вес составляет 42 мг). Коэффициент вариации среднего срока службы компьютеров по данным предыдущих обследований составляет 6%, а вся партия состоит из 1220 электроламп.
|
|
|
Решение
По условию задачи известны:
выборочная средняя – 
мг;
предельная ошибка выборки – 
мг;
коэффициент доверия – 
при вероятности 0,954;
объем партии – 
электроламп;
коэффициент вариации – 
;
Среднее квадратическое отклонение
.
Оптимальная численность выборки для повторного отбора
.
Таким образом, чтобы с заданной вероятность предельная ошибка не превышала 3% среднего значения, необходимо в порядке случайной выборки обследовать 16 электроламп.
|
|
|
