Коэффициент поперечной силы

При проектировании закруглений в плане необходимо обеспечить удобство и безопасность движения. Удобство обеспечивается плавностью движения, БД - достаточной видимостью на кривой и исключением заноса и выброса автомобиля.

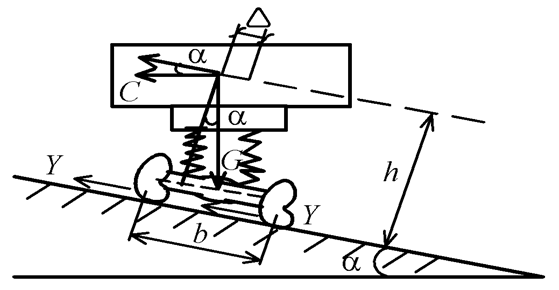
На автомобиль, движущийся по кривой в точке, радиус кривизны которой равен R, действует центробежная сила С = mv 2/ R, где m – масса автомобиля, т; v – скорость, м/с.

m = G/g,

тогда С = G v ²/ gR.

Центробежная сила направлена горизонтально в сторону от центра кривой и стремится сдвинуть автомобиль с ПЧ. Составляющая веса автомобиля противодействует центробежной силе.

Проектируя силы С и G на направление поперечного уклона ПЧ дороги получим общую силу Y, которая стремится сдвинуть автомобиль с дороги, называемую поперечной силой.

Y = С cosα ± G sinα.

Принимая sinα = i и cosα = 1 получим

Y = G v ²/ gR ± G i; Y = G v ²/ gR ± mgi.

Разделим на G и получим

Y/ G = v ²/ gR ± i.

Отношение Y/ G называется коэффициентом поперечной силы - μ.

Поперечная сила отрицательно действует на автомобиль, ухудшает управление и сцепление шин с покрытием.

 

34 Рекомендуемые и наименьшие допустимые радиусы кривых в плане

При проектировании автодорог радиусы кривых в плане определяют по приведенной выше формуле:

R ≥ v ²/ g (μ ± i),

«+» – наименьший радиус;

«–» – рекомендуемый.

Допустимые максимальные значения коэффициента поперечной силы μ в зависимости от поперечного сцепления шины с поверхностью покрытия и исходя из требований устойчивости автомобиля приведем в таблице.

Показатель	Предельно-допустимые значения μ на покрытии
сухом, φ = 0,6	мокром, φ = 0,4	покрытом льдом, φ = 0,2
Устойчивость против опрокидывания	0,6	0,6	0,6
Устойчивость против заноса	0,36	0,24	0,12
Комфортность поездки	0,15	0,15	0,15
Экономичность эксплуатации автомобиля	0,10	0,10	0,10

Рекомендуемый радиус – это такой радиус кривой, который обеспечивает удобное движение автомобиля по кривой с расчетной скоростью. Рекомендуется назначать радиусы ≥ 3000 м, т.к. условия движения на таких кривых такие же, как на прямых, при этом не устраиваются переходные кривые.

В зависимости от рельефа местности, наличия различных препятствий и т.д. приходится допускать меньшие значения радиусов, при этом соблюдается условие, обеспечивающее движение автомобиля с расчетной скоростью с запасом устойчивости против заноса или опрокидывания.

Практика показывает, что в большинстве случаев занос автомобиля происходит раньше, чем его опрокидывание, поэтому минимальные радиусы определяют, как правило, по условиям заноса.

Наименьший радиус – это такой радиус кривой, при котором обеспечивается безопасное движение с расчетной скоростью при чистом и увлажненном покрытии, с устройством виражей и уширением ПЧ.

Наименьшие допустимые радиусы кривых в плане определяют по расчету в зависимости от скорости движения и минимальных значений коэффициента поперечной силы μ.

В соответствии с ТКП установлены следующие значения радиусов кривых в плане в трудных условиях проектирования.

Расчетная скорость движения
Категория дороги	I	II	III	IV	V	-	-	-
Наименьшие радиусы кривых в плане, м

 

 

35-36 Виды закруглений плана трассы

Закругления на автомобильных дорогах бывают:

• состоящее из круговой кривой;
• состоящее из круговой кривой и переходных кривых;
• клотоидное;
• серпантины.

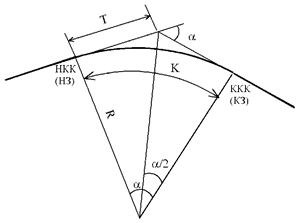
При радиусах более 3000 м переходные кривые не устраиваются, только круговая кривая. Расчет такого закругления производят в следующей последовательности:

определяется угол поворота α; назначается рекомендуемый радиус R; рассчитываются элементы круговой кривой: К; Т; Д; Б; определяется пикетажное значение начала круговой кривой (НКК),

соответствующее началу закругления (НЗ) и конца круговой кривой (ККК), соответствующее концу закругления (КЗ).

При движении по кривым малого радиуса (R ≤ 2000 м) в целях безопасности движения и плавного нарастания центробежного ускорения устраивают переходную кривую. Переходная кривая представляет собой кривую переменного радиуса (от ∞ до R), по которой происходит плавный поворот передних колес автомобиля, исключающий боковой толчок при въезде на круговую кривую. Длина переходной кривой определяется по формуле

L = v ³/(47 RJ),

где v – скорость автомобиля;

R – радиус круговой кривой;

J – скорость нарастания центробежного ускорения.

Расчет закругления с переходными кривыми и круговой вставкой выполняют в следующей последовательности: в зависимости от угла поворота αи радиуса круговой кривой R определяют значения К; Т; Д; Б; в зависимости от радиуса круговой кривой R по таблицам

устанавливаются элементы переходной кривой:

- длина L;

- угол поворота α_min = 2β;

- сдвижка начала круговой кривой t;

-сдвижка круговой кривой р;

• проверяется возможность устройства переходной кривой, α ≥ α_min;
• определяется центральный угол γ и длина сокращенной кривой К ₀

γ = α – 2β;

К ₀ =π R γ/180;

• рассчитываются элементы закругления:

Т₁ = Т + t; К ₁ = К ₀ + 2 L;

Б ₁ = Б + р; Д ₁ = 2 Т ₁ – К ₁;

• определяется пикетажное положение основных точек закругления:

НЗ = ВУ – Т ₁; НКК = НЗ + L;

КЗ = НЗ + К ₁; ККК = КЗ – L.

В качестве переходных кривых на дорогах используют различные кривые: клотоиду, лемнискату Бернулли, кубическую параболу и др. Наибольшее распространение - клотоида. В прямоугольной системе координат клотоида выглядит следующим образом:

ЕЕ траектория в начальной стадии соответствует равномерному поступательному движению автомобиля при вращении руля с одинаковой угловой скоростью. Для удобства проектирования клотоиды используют шаблоны, выполненные в масштабе карты.

В настоящее время при проектировании автодорог широко применяется клотоидное закругление - это закругление, состоящее из двух переходных кривых. Расчет клотоидного закругления выполняется с использованием специальных таблиц для проектирования и разбивки клотоидной трассы. Переходные кривые по клотоиде характеризуются: углом поворота трассы α, углом клотоиды β, длиной клотоиды L, тангенсом клотоиды Т, радиусом R, параметром клотоиды А = √(RL).

При трассировании дорог в горной местности широко применяется закругление в виде серпантины. Серпантина – это кривая, описанная с внешней стороны угла поворота между двумя ее направлениями, сходящимися под острым углом.

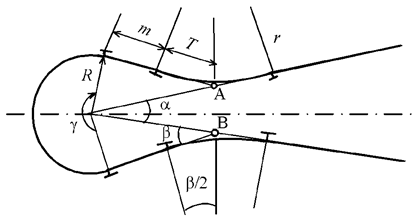
Основные элементы серпантины: основная кривая с углом γ и радиусом R; вспомогательные кривые с углом β и радиусом r; прямая вставка – m; шейка серпантины - АВ

Серпантины могут быть I рода – симметричные, у которых обратные кривые расположены выпуклостью в разные стороны (см. рисунок) и IIрода – со смещенным центром основной кривой и обратными кривыми, описанными дугами разных радиусов.

Проектирование серпантины заключается в расчете ее элементов и проверке размещения ее на местности.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: