 |
Опыты Рейнольдса. Критически ечисла Рейнольдса. Определение числа Рейнольдса.
|
|
|
|
При проведении многочисленных экспериментов с потоками движущейся жидкости было неоднократно подмечено, что на величину гидравлических сопротивлений кроме физических свойств самой жидкости, формы и размеров каналов, состояния их стенок, существенное влияние оказывает особенности движения частиц жидкости в потоке.
Впервые дал теоретическое обоснование этой зависимости английский физик Осборн Рейнольде. Суть его эксперимента заключалась в следующем.
В ёмкость А достаточного большого объёма была вставлена длинная (не менее 20 диаметров) стеклянная трубка Г. На конце этой трубки устанавливался кран Д для регулирования расхода жидкости. Измерение расхода жидкости осуществлялось с помощью мерной ёмкости Б, расположенной в конце трубки. Из малого бачка В с помощью тонкой изогнутой трубки Е по центру основной трубки вводилась подкрашенная жидкость. Её расход также регулировался с помощью краника. Уровень жидкости в основном баке А поддерживался постоянным. Плавно меняя расход жидкости в трубке, Рейнольдс отметил, что при малых скоростях движения жидкости подкрашенная струйка жидкости текла по центру потока жидкости, не смешиваясь с остальной жидкостью потока Однако при определённой скорости жидкости подкрашенная струйка жидкости теряла свою устойчивость и, в конечном итоге частицы окрашенной жидкости перемешивались с остальной жидкостью. При снижении скорости движения жидкости положение восстанавливалось: хаотичное движение частиц жидкости снова становилось упорядоченным. Рейнольдс менял длину и диаметр трубки, вязкость жидкости, количество подкрашенных струек жидкости и установил, что эффект перемешивания (смена режима течения жидкости) зависит от скорости движения жидкости, её вязкости и от диаметра трубки, причём при увеличении вязкости жидкости для смены режима течения жидкости требовалась большая скорость Отсюда Рейнольдс сделал вывод что смена режима движения жидкости зависит от целого комплекса параметров потока а именно от соотношения:
|
|
|
которое получило название числа Рейнольдса Число Рейнольдса оказалось безразмерной величиной представлявшей собой отношение сил инерции к силам вязкостного трения. Была установлена и критическая величина числа Рейнольдса, при котором происходила смена режима движении жидкости R.eкрн она оказалась равной 2320.и R.eкрв=4000.
Потери напора. Определение потерь напора по длине при ламинарном режиме движения. Вывод ур-я Пуазейля. З-н Пуазейля.
Соединим в ур-е Бернули сеч 11 и 22
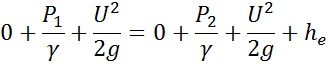
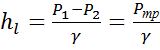(1)
Запишем ур-е равномер движения выделенного объема
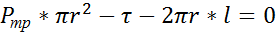(2)
Решим 2 относительно τ
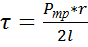(3)
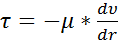(4)
Сравним (3) и (4)
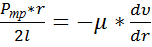(5)
Разделим переменные
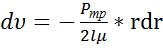(6)
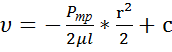(7)
Постоянную интегр найдем из усл нахождения в т. А
Для т. А: U=0 V=V0
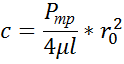
Подставим с в ур-е (7)
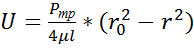(8)
Расчит элементарный расход через основание цилиндра
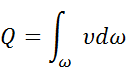
Подст ур-е (8)
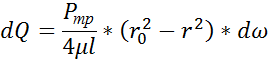
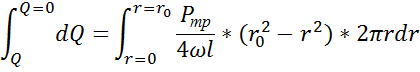
Проинтегр ур-е
ур-е для опред расхода при ломинар р-ма
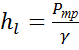
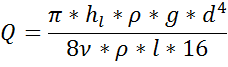
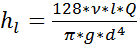ур-е Пуазейля
Закон Пуазейля
Потеря напора в слож ломинар движения прямо пропорц расходу и кинематич коэф вязкости и обратнопропорц диаметру в 4-ой степени.
Из ур-я Пуазейля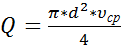 
Заменив в Q получим окон чур-е Вейсбаха-Дарси
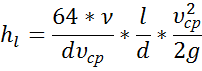
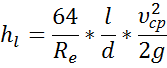
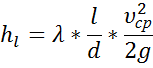
Ур-е Вейсбаха-Дарси. Крэффиц Дарси для ламинар движ.
Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D,
где λ — коэффициент потерь на трение по длине.
Тогда формула Дарси приобретает вид:
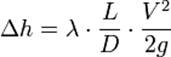
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:
где Re — число Рейнольдса.
|
|
|
|
|
|
