 |
ДУ движущейся идеальной жидкости (ур. Эйлера)
|
|
|
|
Для вывода уравнения движения жидкости обратимся к записанному ранее уравнении равновесия жидкости (в проекциях на координатные оси), иначе говоря: 
Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодействующая отлична от 0,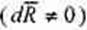 
то жидкость начнёт двигаться с некоторой скоростью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, составляющие жидкое тело получат ускорение.
Тогда уравнение движения жидкости в проекциях на координатные оси можно записать в следующем виде:
Согласно основному положению о поле скоростей (метод Эйлера) для проекций скоростей движения жидкости можно записать следующее:
или (для установившегося движения жидкости):
Найдём первые производные от скоростей по времени, т.е. определим ускорения вдоль осей координат:
отметим, что:
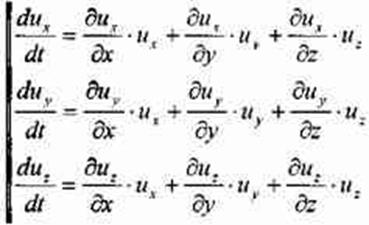
Теперь подставив выражения для ускорений в исходную систему дифференциальных уравнений движения жидкости, получим систему уравнений Эйлера в окончательном виде:
При неустановившемся движении жидкости уравнения Эйлера дополняются первыми слагаемыми.
33.Определение скорости и расхода при истеч жидкости через малые отверстия в тонкой стенке при постоян расходе. Коэф сжатия скорости и расхода. Уравнение Торичелли.
Скорость истечения жидкости через отверстие такое отверстие
где Н - напор жидкости, определяется как
φ- коэффициент скорости
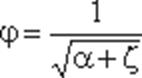
где α - коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Степень сжатия оценивается коэффициентом сжатия.
где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dс и dо - диаметры струи и отверстия соответственно.
|
|
|
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
Закон Торричелли утверждает, что скорость истечения, v, жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубине h от поверхности, эта скорость такая же, как и у тела, свободно падающего с высоты h, то есть
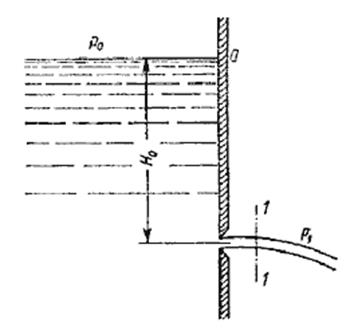
Истечение жидкости под уровень через малое отверстие в тонкой стенке.
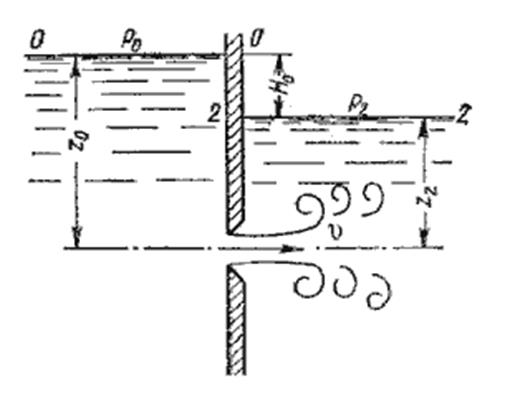Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
где φ - коэффициент скорости;
Н - расчетный напор,
Расход жидкости равен
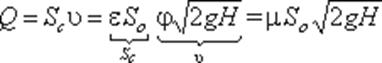Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
Определение времени опорожнения сосуда.
Считаем, что давление плавно изменяется, хотя оно установившееся. Значит за некоторый промежуток времени Δt уровень опуститься на Δh.
Объем жидкости, вышедший из резервуара за Δt:
После интегрирования и подстановки пределов получаем:
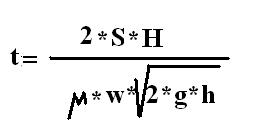
А для постоянного напора:
При постоянном напоре время заполнения резервуара в 2 раза меньше, чем при переменном.
|
|
|
