 |
Изменение результирующей теплового баланса и температуры воды на участке реки
|
|
|
|
Факторы формирования термического режима рек
Изменение теплосодержания Δ q, Дж, объема воды V на участке реки определяется формулой:
Δ q = C ρΔθ V, (2.1)
где С – теплоемкость воды, Дж/(кг×0С), ρ – плотность воды, кг/м3, Δθ – изменение температуры воды, 0С. Из (2.1) следует, что изменение температуры воды за некоторый интервал времени
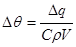. (2.2)
Считая, что С, ρ, V – постоянные, можно сказать, что изменение температуры воды θ пропорционально изменению теплосодержания водной массы q. Если изменение теплосодержания Δ q > 0, то изменение температуры воды Δθ > 0. В противоположном случае Δθ < 0, а Δ q < 0.
Изменение теплосодержания d q объема воды V связано с уравнением теплового баланса для участка реки (рис. 2.1):
Q н - Q в = d Q = – d q, (2.3)
где Q в – количество тепла, поступающее на верхнюю границе участка реки (адвекция), Q н – количество тепла, уходящее через нижнюю границу, d Q – изменение потока тепла, d q – изменение теплосодержания водной массы. Если d Q > 0 (уходит тепла больше, чем приходит), то d q < 0 – теплосодержание водной массы уменьшается, а ее температура θ понижается. В соответствии с уравнением (2.2) при d Q < 0 (тепла поступает больше, чем уходит) d q > 0 – теплосодержание водной массы увеличивается и, соответственно, повышается температуры воды Δθ > 0. Таким образом, в рассматриваемой тепловой системе величина d Q однозначно определяет изменение d q и Δθ.
Участки рек – открытые системы и d Q = – d q 
0. Если уравнение (2.3) универсально, то уравнение, раскрывающее причины возникновения 
(уравнение результирующей баланса тепла), отражает специфические условия, влияющие на величину d Q и d q, т.е.
|
|
|
d Q = – dq = А + В + С, (2.4)
где А, B, C – приходные и расходные составляющие теплового баланса (Михайлов, Добровльский, Добролюбов, 2007). С учетом (2.1) и (2.3) получаем:
Δθ= - 
, (2.5)
где А – тепловой поток на границе «водная поверхность – воздух», В- тепловой поток на границе «вода – русло реки», С – внутренние источники поступления или расхода тепла.
А = R 
+ Θx + Θк – Θи, (2.6)
где R – радиационный баланс водной поверхности,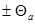 
– теплообмен с атмосферой, Θx – тепло, поступающее с атмосферными осадками, Θк – поступление тепла при конденсации, Θи – расход тепла на испарение воды.
Теплообмен с руслом реки включает
В = 
Θгр, (2.7)
где 
– поступление или отток тепла с грунтовыми водами, Θгр – теплообмен с ложем водного объекта.
Величина
С = Θд Θф Θхим Θб, (2.8)
где Θд – тепло, обусловленное диссипацией гидравлической энергии, Θф – энергию фазовых переходов, Θхим и Θб – приход или расход тепла при химических и биохимических процессах.
Наибольшее влияние на изменение теплосодержания водной массы оказывают процессы на границе «вода – воздух». Они влияют на приток солнечной радиации и теплообмен с прилегающими слоями воздуха. Радиационный баланс водной поверхности:
R = I – I эф = (1- Aa) (Q пр+ q рр) – I эф, (2.9)
где I – поглощенная суммарная солнечная радиация, I эф – эффективное излучение воды, (Q пр+ q рр) – суммарная солнечная радиация при безоблачном небе, Q пр – прямая солнечная радиация, q рр – рассеянная солнечная радиация, А a – альбедо водной поверхности (Хромов, Петросянц, 2001).
Интенсивность суммарной радиации меняется с высотой Солнца, с высотой местности над уровнем моря, а также зависит от прозрачности атмосферы, облачности и других факторов. Интенсивность солнечной радиации при безоблачном небе I 0 = (Q пр + q рр)0 для любой точки земного шара и любого часа года может быть оценено по формуле:
|
|
|
(2.10)
где r 0 и r – среднее в данный момент времени расстояние от Земли до Солнца, S 0 – солнечная постоянная, h c – высота стояния Солнца, 
ρс – плотность субстанций в атмосфере, αр – коэффициент рассеяния радиации.
При наличии облаков суммарная радиация определяется по формуле:
I = I 0[1 – (a 1 – b 1 n 0) n 0], (2.11)
где n 0 – общая облачность, в долях единицы, b 1 = 0,38, а 1 – коэффициент, зависящий от широты местности (Винников, Проскуряков, 1988).
Эффективное излучение воды I эф это разница между собственным излучением водной поверхности I с и встречным излучением атмосферы I а:
I эф = I c – I a. (2.12)
Величина I с определяется с использованием закона Стефана-Больцмана для абсолютно черного тела:
I а.ч.т. = σ Т 4, (2.13)
где постоянная σ = 5,7×10-8 Вт/(м2×К4), Т – абсолютная температура воды, К (Хромов, Петросянц, 2001). Так как вода не абсолютно черное тело, то для расчета ее собственного излучения правую часть выражения (2.13) умножают на поправочный коэффициент «серости» тела δв, который для воды меняется от 0,95 до 0,963 при изменении ее температуры θ в диапазоне 0 
1000С (Винников, Проскуряков, 1988).
Теплообмен между поверхностью воды и воздухом осуществляется (при отсутствии льда) за счет механизма конвективной теплопередачи и определяется по «закону» Ньютона (Алексеевский, 2006):
q k = -α (θ – θв), (2.14)
где qk – поток тепла через единицу площади водной поверхности, θ – температура воды, θв – температура воздуха, α – коэффициент теплоотдачи. Этот коэффициент зависит от ряда факторов, влияющих на интенсивность теплоотдачи:
α = 2,65 [1 + 0,8 w + f (Δθ)], (2.15)
где w – скорость ветра на высоте 2 метра, м/с; f (Δθ) – функция, зависящая от разности температур θ-θB (Винников, Проскуряков, 1988). Если θ-θB > 0, то d q k < 0 и водная масса охлаждается. Если θ-θB < 0, то d q k > 0 и вода нагревается в соответствии с уравнением (2.2).
Тепло, поступающее с атмосферными осадками Θx, определяется по формуле:
Θx = C ρθос Sx, (2.16)
где С – теплоемкость воды, Дж/(кг×0С); ρ – плотность воды, кг/м3; S – площадь зеркала воды, км2; x – слой осадков, мм; θос – средняя температура атмосферной влаги.
|
|
|
Влияние поступления тепла с атмосферными осадками на температуру речной воды выражается повышением или понижением температуры воды в зависимости от знака разности температур речной воды и атмосферных осадков. Если θос<θ, то происходит охлаждение речной воды. Если θос>θ, то происходит увеличение удельного теплосодержанияводной массы q у (Дж/м3). Если рассматривать теплоту как консервативную примесь, то
, (2.17)
где q y . p – удельное теплосодержание воды реки до поступления осадков, Wp – объем воды на данном участке реки, x – количество осадков, мм, S – площадь водной поверхности, Qy . oc – удельное теплосодержание осадков.
Затраты или поступление теплоты в водную массу в случае испарения или конденсации водяного пара:
Θконд= Θисп= L и m = L и E ρ, (2.18)
где m – масса испаряемой или конденсируемой влаги; E – слой испарившейся (сконденсировавшейся) воды за единицу времени, м/ч; ρ – плотность воды, кг/м3; L и – удельная теплота испарения, Вт×ч/кг. Последняя величина зависит от температуры испаряющей поверхности θп (Алексеевский, 2006):
L и = (25 – 0,024θп)× 105, (2.19)
где 25×105 Дж – удельная теплота испарения при температуре поверхности воды 00С. Количество испарившейся воды может быть рассчитано, например, по формуле Б.Д. Зайкова (Винников, Проскуряков, 1988). Тогда, с учетом (2.18), количество теплоты, теряемое водой при испарении, равно:
Q и = 4,1 (1 + 0,72 w 2) (e 0- e 2), (2.20)
где w 2 – скорость ветра на высоте 2 м над поверхностью воды, e 0 – давление насыщенного водяного пара в воздухе при температуре испаряющей поверхности, e 2 – парциальное давление водяного пара на высоте 2 м.
Большое влияние на температуру воды на участке реки в некоторых случаях имеют тепловые потоки на границе «вода – русло реки». Охлаждение или нагревание грунтовыми водами речных вод (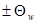
) связано с процессами смешения вод разного генезиса. Считая теплоту консервативной примесью (по аналогии с формулой 2.17) получаем:
|
|
|
, (2.21)
где q y . p – удельное теплосодержание воды на участке реки выше зоны выклинивания (впадения) грунтовых вод, Vp = V 0+ dV в, где V 0 – объем воды на участке реки в начальный момент времени, d V в – объем воды, дополнительно поступающий на участок реки за время d t через верхний створ, V гр – объем грунтовых вод, поступающих на данный участок реки за промежуток времени d t, qy . oc – удельное теплосодержание грунтовых вод.
Теплообмен водной массы с ложем водного объекта происходит по закону Ньютона (Винников, Проскуряков, 1988):
q k = -α (θ-θгр), (2.22)
где q k – поток тепла через единицу площади дна, θ – температура воды, θгр – температура грунтов, α – коэффициент теплоотдачи (зависящий в данном случае от разности температур воды и грунта, скорости потока, свойств грунта и т.п.). Если температура воды в реке выше, чем температура ее русла θ > θгр, то qk < 0 и, в соответствии с (2.2), температура воды реки понижается, нагревая русло реки. Если θ < θгр, то qk < 0 и вода в реке нагревается, а ложе реки охлаждается.
|
|
|
