 |
Изменение температуры воды по длине реки
|
|
|
|
Изменение температуры воды вдоль рек можно рассматривать с двух позиций. В первом случае можно считать изменение температуры воды непрерывной функцией расстояния. Во втором случае, распределение температуры воды вдоль потока описывается дискретной функцией. Применение такой формализации является вынужденным, но близким к реальным условиям измерений температуры воды, которые всегда являются дискретными.
В связи с условиями дискретности измерений и принятой модели однородности температуры воды на некотором участке реки, можно описывать изменение теплосодержания и температуры воды вдоль реки дискретной функцией. Эта функция зависит от множества факторов, которые рассмотрены в гл. 2 и разд. 6.1. Так как факторов формирования термического режима много, а данные о них мало, то одним из путей изучения продольной изменчивости температуры воды может быть поиск статистических зависимостей между ее величиной в произвольном створе реки и температурой воды на участках реки, удаленных от начального створа на расстояние x1, x2,….xm.
В работе изучены статистические связи между температурой воды на разных постах некоторых рек севера ЕТР. Для этого использованы данные из гидрологических ежегодников о ежедневных температурах воды за периоды весеннего нагревания (температуры воды выше 100С) и осеннего охлаждения (температуры воды ниже 100С) в 1961–1964 гг. Для анализа привлекались данные о температуре 3 рек: Вологды (приток Сухоны), Сухоны (составляющая Малой Северной Двины) и собственно Северной Двины. Температура воды в нижерасположенных створах этих рек может быть связана с температурой воды выше по течению, поскольку они образуют единую русловую сеть (рис. 6.3). В табл. 6.6 посты этих водотоков имеют общую последовательную нумерацию.
|
|
|
Связь между температурой воды на смежных постах одной реки обусловливается адвекцией тепла с участка, где расположен вышерасположенный пост, теплообменом с грунтами и атмосферой. Наличие фактора адвекции тепла подразумевает, что температура воды на нижерасположенном участке зависит от температуры участков выше по течению. На средних и крупных реках фактор адвекции тепла играет основную роль, поэтому связь между сопоставляемыми температурами может прослеживаться на протяженных участках рек (Одрова, 1987). Вследствие этого существует прогнозный потенциал поиска статистических зависимостей вида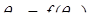 
, где θнп – температура воды на нижерасположенном, θвп – температура воды на вышерасположенном посту.
Таблица 6.6. Характеристики постов, данные по которым использованы при анализе пространственной связанности ежедневной температуры воды
| Река | № поста | Название поста | Расстояние до устья, км | Расстояние между постами, км | Площадь бассейна реки у поста, км2 |
| Вологда | 1 | Вологда | 1413 | - | 2800 |
| Сухона | 2 | Наремы | 1176 | 237 | 23700 |
| 3 | Тотьма | 1006 | 170 | 34900 | |
| 4 | Каликино | 767 | 239 | 49200 | |
| 5 | Великий Устюг | 732 | 35 | 50300 | |
| Северная Двина | 6 | Котлас | 663 | 69 | 89300 |
| 7 | Абрамково | 520 | 143 | 223000 | |
| 8 | Березник | 346 | 174 | 280000 | |
| 9 | Усть-Пинега | 131 | 215 | 350000 |
Температуру воды на участке реки или обеспечивать несовпадающее воздействие на эту характеристику теплового состояния водной массы выше и ниже по течению. Кроме того, впадение притоков влияет на температуру воды ниже узла слияния. В результате температура воды на смежных постах одной реки зависит от поступления воды с верхнего участка, местных факторов и боковой приточности.
Все факторы можно поделить на три группы. Первая группа – общая для обоих постов, влияет на температуру воды одновременно, порождаят некоторую синхронность колебаний температур. Вторая и третья группы факторов влияет на тепловое состояние реки в районе одного из постов. Адвекция тепла с вышележащих участков относится к факторам первой группы. Теплообмен с грунтами является местным фактором, поэтому относится ко второй и третьей группе факторов. Влияние теплообмена с атмосферой в зависимости от текущих синоптических условий может относиться к любой группе факторов.
|
|
|
Связь 
, вследствие вышесказанного, может быть представлена линейной функцией соответствующего значения температуры θвп и независимого параметра zi:
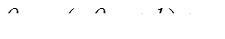(6.17)
где а и b – параметры линейной функции. Параметр zi зависит от факторов второй и третьей группы, а коэффициенты a и b от факторов первой группы.
Параметры уравнения регрессии 
устанавливаются методом наименьших квадратов
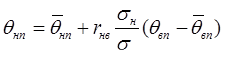, (6.18)
где 
– средние; 
– стандарты; 
- коэффициент корреляции между температурой воды в районе верхнего и нижнего створов. Каждая точка регрессии θнп по θвп есть центр условного распределения зависимой переменной при данном значении θвп (Евстигнеев, 1990). Вычисляя θнп по уравнению регрессии как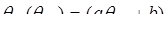 
, получаем не календарную величину θнп, а ее условное математическое ожидание. Рассеяние возможных значений θнп i относительно 
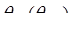характеризуется условным стандартом
. (6.19)
Этот показатель является характеристикой среднего отклонения реальных значений температуры относительно вычисленных по уравнению регрессии, обусловленного отсутствием учета факторов второй и третьей группы при построении уравнения регрессии.
Среднеквадратическое отклонение линейно зависимой от θвп составляющей θнп может быть вычислено как:
. (6.20)
Равенство (6.20) означает, что величина θнп, рассчитанная по уравнению регрессии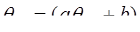 
, преуменьшает размах отклонений по сравнению с наблюденными значениями с коэффициентом пропорциональности 
.
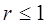Суммарная дисперсия фактических значений θнп ввиду независимости линейной и случайной составляющих может быть записана как
|
|
|
. (6.21)
Из выражения (6.21) видно, что преуменьшение размаха колебания величин температуры воды, рассчитанных по уравнению регрессии, по сравнению с фактическими значениями происходит из-за выпадения составляющей дисперсии, вызываемой факторами, не зависящими от колебаний температуры воды у верхнего поста (Евстигнеев, 1990).
Характеристикой тесноты связи могут быть коэффициент корреляции r и суммарное среднеквадратическое отклонение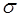 
(вычисляется как квадратный корень из правой части уравнения 6.21).
Для составления уравнения регрессии необходимо, чтобы выполнялись определенные требования к рядам наблюдений. Например, ряды наблюдений должны быть одинаковой длины. Так как на разных постах измерения температуры воды начинаются (весной) и заканчиваются (осенью) в зависимости от даты начала и конца ледостава, неодинаковой для разных створов, то ряды значений температуры обычно имеют разную длину.
Чтобы устранить этот недостаток, при вычислении статистических характеристик часть данных отсеивалась. Первым номером в весенней части рядов наблюдений отмечалась температура воды в день, когда температура воды на обоих постах хотя бы один раз за этот год превышала 00С. Конец весеннего этапа наблюдений также часто не совпадает для разных постов – температура 100С достигается на разных постах в разные даты. В связи с этим принималось, что конечным элементом «весенней» выборки является дата, когда температура воды на одном из створов оказывается больше 100С. Аналогичная логика применялась и для осеннего этапа наблюдений: начальным элементом рядов назначались температуры за начальную дату измерений того поста, на котором наблюдения начались позднее. Конечным элементом «осенней» выборки для обоих рядов наблюдений назначалась температура, измеренная за дату последней положительной температуры на одном из постов. После этого «весенние» и «осенние» части выборки объединялись. Считая, что характер связи за дни с различной средней температурой воды на отдельно взятом посту не изменяется, можно объединить заранее обработанные по этой схеме температуры воды в единый ряд наблюдений. Это позволяет вычислить статистические характеристики и обосновать уравнения регрессии для любых смежных постов на одной реке.
|
|
|
Одновременно появляются возможности для установления роли адвекции тепла с вышележащих участков и факторов, преобразующих теплосодержание водной массы при переходе от одного участка к другому. Для этого рассчитывались статистики двух рядов температуры со смещением во времени, равным времени добегания речных вод от одного створа реки до другого. В этом случае, при использовании уравнения регрессии, разница фактической температуры θвп и рассчитанной температуры θнп может характеризовать изменение теплосодержания водной массы за счет влияния факторов первой группы. Разница рассчитанной θнп и фактической температуры θнп будет характеризовать влияние местных факторов. Статистической характеристикой, позволяющей оценить влияние местных факторов одной цифрой, является условное среднеквадратическое отклонение, вычисляемое в соответствии с (6.19).
Таблица 6.7. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двин
| Номера постов | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 0,952 | 0,959 | 0,911 | 0,938 | 0,918 | 0,913 | 0,897 | 0,719 |
| 2 | 0,952 | 1 | 0,901 | 0,823 | 0,872 | 0,900 | 0,841 | 0,827 | 0,562 |
| 3 | 0,959 | 0,901 | 1 | 0,961 | 0,976 | 0,941 | 0,953 | 0,946 | 0,770 |
| 4 | 0,911 | 0,823 | 0,961 | 1 | 0,991 | 0,967 | 0,965 | 0,958 | 0,838 |
| 5 | 0,938 | 0,872 | 0,976 | 0,991 | 1 | 0,981 | 0,981 | 0,963 | 0,812 |
| 6 | 0,918 | 0,900 | 0,941 | 0,967 | 0,981 | 1 | 0,983 | 0,953 | 0,766 |
| 7 | 0,913 | 0,841 | 0,953 | 0,965 | 0,981 | 0,983 | 1 | 0,973 | 0,772 |
| 8 | 0,897 | 0,827 | 0,946 | 0,958 | 0,963 | 0,953 | 0,973 | 1 | 0,803 |
| 9 | 0,719 | 0,562 | 0,770 | 0,838 | 0,812 | 0,766 | 0,772 | 0,803 | 1 |
Логично предположить, что наиболее тесные связи могут соответствовать ситуациям, при которых учитывается время добегания. Однако этот факт требует статистического доказательства, поэтому расчеты были проведены для разных периодов смещения рядов относительно друг друга: от 0 до 5 дней.
Вычисление коэффициентов корреляции без смещения рядов (табл. 6.7) показало, что, в целом, теснота связи ослабевает при увеличении расстояния между постами. Однако такая закономерность наблюдается не всегда, например, связь между температурами воды на постах 1 и 4 менее тесная по сравнению с аналогичными зависимостями для условий корреляции данных по первому посту и постами №№5,6,7. Это, вероятно, связано с влиянием местных условий изменения температуры воды, а также влиянием притоков, термическое состояние которых сформировалось относительно южнее или севернее.
|
|
|
Расчет соответствующих условных среднеквадратических отклонений в соответствии с формулой (6.19) показал (табл. 6.8), что средняя ошибка, связанная с пренебрежением учета влияния местных факторов, также возрастает при увеличении расстояния между постами, меняется от 0,390С (для корреляции данных по постам №№4 и 5) до 2,13 0С для анализа ситуации по постам №№2 и 9.
Таблица 6.8. Условные стандарты отклонений для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,923 | 0,950 | 0,922 | 0,944 | 0,918 | 0,911 | 0,907 | 0,743 |
| 2 | - | - | 0,908 | 0,864 | 0,900 | 0,921 | 0,859 | 0,853 | 0,609 |
| 3 | - | - | - | 0,956 | 0,969 | 0,925 | 0,939 | 0,940 | 0,801 |
| 4 | - | - | - | - | 0,966 | 0,940 | 0,939 | 0,933 | 0,859 |
| 5 | - | - | - | - | - | 0,956 | 0,961 | 0,947 | 0,838 |
| 6 | - | - | - | - | - | - | 0,968 | 0,945 | 0,802 |
| 7 | - | - | - | - | - | - | - | 0,961 | 0,814 |
| 8 | - | - | - | - | - | - | - | - | 0,840 |
|
| - | - | - | - | - | - | - | - | - |
Смещение рядов на один день увеличивает степень статистической связи между температурой воды на большей части постов, поскольку для части постов это смещение равно времени добегания. При учете такого времени добегания привело к увеличению коэффициентов корреляции для связей между постом Наремы (2) и всеми нижележащими постами; для связей температуры всех постов с температурой воды у поста Усть-Пинега (9); для связей между рядом поста Вологда (1) и постами №№4, 5, 8.
Увеличение коэффициента корреляции для постов №№1–4, 1–5, 1–8 невелико, в среднем на 0,009. Для половины постов (18 из 36) учет времени добегания не привел к увеличению коэффициентов линейной корреляции, наоборот, они даже уменьшились. Таким образом, в большинстве случаев температура воды от одного поста до другого претерпевает изменения, снижающие роль процессов добегания водных масс. Это означает, что основным фактором, определяющим закономерное изменение температуры воды на разных постах, является синоптическая обстановка в районе постов, а не адвекция тепла.
Таблица 6.9. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,877 | 0,933 | 0,914 | 0,935 | 0,893 | 0,894 | 0,905 | 0,759 |
| 2 | - | - | 0,903 | 0,877 | 0,908 | 0,923 | 0,868 | 0,869 | 0,648 |
| 3 | - | - | - | 0,930 | 0,944 | 0,881 | 0,907 | 0,931 | 0,820 |
| 4 | - | - | - | - | 0,923 | 0,895 | 0,901 | 0,904 | 0,868 |
| 5 | - | - | - | - | - | 0,913 | 0,930 | 0,926 | 0,852 |
| 6 | - | - | - | - | - | - | 0,939 | 0,926 | 0,825 |
| 7 | - | - | - | - | - | - | - | 0,932 | 0,841 |
| 8 | - | - | - | - | - | - | - | - | 0,864 |
| 9 | - | - | - | - | - | - | - | - | - |
Увеличение смещения рядов ежедневной температуры воды до двух дней приводит к возрастанию коэффициентов корреляции между температурой воды у поста Наремы (2) и постами №№4,5,6,7,8. Таким образом, в данном случае адвекция тепла оказывает определяющую роль на синхронность изменения температуры воды. Увеличение коэффициентов корреляции также произошло и для связей температуры воды всех постов с температурой у поста Усть-Пинега (9) в среднем на 0,054 по сравнению расчетом без учета добегания.
Таблица 6.10. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,822 | 0,909 | 0,893 | 0,913 | 0,856 | 0,867 | 0,891 | 0,765 |
| 2 | - | - | 0,889 | 0,878 | 0,904 | 0,914 | 0,870 | 0,872 | 0,679 |
| 3 | - | - | - | 0,899 | 0,914 | 0,833 | 0,878 | 0,912 | 0,829 |
| 4 | - | - | - | - | 0,875 | 0,845 | 0,861 | 0,869 | 0,871 |
| 5 | - | - | - | - | - | 0,862 | 0,898 | 0,900 | 0,861 |
| 6 | - | - | - | - | - | - | 0,902 | 0,897 | 0,839 |
| 7 | - | - | - | - | - | - | - | 0,893 | 0,858 |
| 8 | - | - | - | - | - | - | - | - | 0,875 |
| 9 | - | - | - | - | - | - | - | - | - |
Расчет коэффициентов корреляции при смещении рядов на три дня показал, что для связи температуры воды на постах №№2–4, 2–7, 2–8 коэффициент корреляции увеличивается в сравнении с расчетом при смещении рядов на два дня. Однако это увеличение очень мало, в среднем 0,002. И в данном случае адвекция тепла имеет наибольшее значение для объяснения продольной изменчивости температуры воды. Уменьшение коэффициентов корреляции для случая обоснования связей между температурами воды на постах №№2–5 и №№2–6 показывает, что наибольшее влияние адвекции тепла возникает при сдвиге членов сопоставляемых рядов на два дня. Также наблюдается повышение коэффициентов корреляции для связей температуры воды на всех постах с температурой воды в районе г. Великий Устюг. Средняя величина увеличения коэффициентов корреляции по сравнению с расчетом при смещении рядов на 2 дня составляет 0,012.
Расчет коэффициентов корреляции при смещении рядов на 4 дня подтвердил гипотезу о наилучшей связанности температур воды для постов №№2–4, 2–7 и 2–8 при сдвиге рядов на 3 дня, так как значения соответствующих коэффициентов корреляции в таблице 6.11 уменьшаются по сравнению с данными таблицы 6.10. Незначительное увеличение коэффициентов корреляции для связей между постами №№3–9, 5–9, отсутствие изменения коэффициентов корреляции для связей между температурой воды в районе постов №№6–9 и 7–9 при увеличении смещения рядов температуры воды на 4 значения свидетельствует о том, что при такой величине смещения влияние адвекции учитывается наиболее полно. Уменьшение коэффициентов корреляции по сравнению с расчетом для сдвига рядов на 3 дня для условий сопоставления данных по постам №№1–9, 4–9, 8–9 говорит о том, что влияние адвекции тепла с вышележащих участков наиболее полно учитывается для этих связей при смещении рядов наблюдений на 3 дня. Увеличение коэффициента корреляции для связи между постами 2 и 9 на 0,24 при увеличении величины смещения рядов с 3 до 4 дней свидетельствует о том, что адвекция тепла учитывается не в полной степени. Расчеты показали, что при смещении рядов наблюдений на 7 дней между температурами постов Наремы (2) и Великий Устюг (9) наблюдается наибольшая степень статистической связанности.
Таблица 6.11 Коэффициенты корреляции для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 |
| 0,754 | 0,877 | 0,863 | 0,884 | 0,807 | 0,832 | 0,865 | 0,763 |
| 2 |
|
| 0,863 | 0,860 | 0,886 | 0,887 | 0,854 | 0,863 | 0,703 |
| 3 |
|
|
| 0,860 | 0,877 | 0,776 | 0,833 | 0,880 | 0,832 |
| 4 |
|
|
|
| 0,826 | 0,791 | 0,816 | 0,829 | 0,865 |
| 5 |
|
|
|
|
| 0,809 | 0,860 | 0,867 | 0,863 |
| 6 |
|
|
|
|
|
| 0,858 | 0,861 | 0,839 |
| 7 |
|
|
|
|
|
|
| 0,847 | 0,857 |
| 8 |
|
|
|
|
|
|
|
| 0,868 |
| 9 |
|
|
|
|
|
|
|
|
|
Оценки условных стандартов расчетных рядов θ для связей между температурами воды на разных постах показали, что наименьшие их величины достигаются при такой величине сдвига рядов температуры воды, при которой достигаются максимальные коэффициенты корреляции. Этот факт доказывает достоверность выполненных расчетов, так как упомянутые две величины связаны по определению. В результате расчетов получено, что наименьшие условные среднеквадратические отклонения колеблются в пределах от 0,399 для связи между постами Каликино (4) и Великий Устюг(5) до 1,88 для связи между постами Вологда (1) и Усть-Пинега (9).
Таким образом, для построения наилучших статистических связей между ежедневными температуры воды на разных постах рр. Вологда, Сухона и Северная Двина необходимо «сдвигать» ряд данных по посту, расположенному ниже по течению реки, на некоторое число дней в соответствии с табл. 6.12. Это число дней является периодом заблаговременности прогноза температуры воды на нижерасположенных створах по данным о температуре воды на вышерасположенных створах.
Таблица 6.12. Смещение рядов ежедневных температур воды для построения наилучших статистических связей между ними
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 4 |
| 2 |
|
| 1 | 3 | 2 | 2 | 3 | 3 | 7 |
| 3 |
|
|
| 0 | 0 | 0 | 0 | 0 | 4 |
| 4 |
|
|
|
| 0 | 0 | 0 | 0 | 3 |
| 5 |
|
|
|
|
| 0 | 0 | 0 | 3 |
| 6 |
|
|
|
|
|
| 0 | 0 | 4 |
| 7 |
|
|
|
|
|
|
| 0 | 3 |
| 8 |
|
|
|
|
|
|
|
| 3 |
| 9 |
|
|
|
|
|
|
|
|
|
Заключение
Основные результаты исследования:
1. В работе рассмотрены основные механизмы воздействия природных факторов на пространственно-временную изменчивость температуры воды в руслах рек.
2. В термическом режиме рек в зоне умеренного климата предложено отказаться от выделения периода открытого русла и ледостава и рассматривать фазы весеннего нагревания, летнего нагревания, фазы осеннего охлаждения и зимнего устойчивого низкотемпературного состояния.
3. Из уравнения турбулентной теплопроводности впервые получены формулы для характеристики распределения температуры воды по глубине рек. Установлено, что вид эпюры местных температур воды не зависит от вертикального распределения скорости потока. Выполнена оценка параметров полученного уравнения и определена эффективность его использования в некоторых природных условиях.
4. Предложена типизация эпюр температуры воды в зависимости от характера теплообмена водной массы с атмосферой и грунтами.
5. Впервые получена зависимость для описания поперечного распределения поверхностной температуры воды. Оценены параметры этой зависимости и ее точность на основе сравнения расчетных и фактических данных об изменении температуры воды по ширине рр. Ока, Волга, Вазуза, Протва и Исьма.
6. Проверена возможность использования уравнения теплового баланса участка реки для характеристики изменения температуры воды по длине р. Сухоны. Установлено, что оно обеспечивает достаточно точные оценки продольной изменчивости температуры воды на участках рек с длиной до 270 км, когда используются метеорологические данные на верхней или нижней границах участка реки.
7. Выявлено, что ежедневная температура воды в верховьях, в среднем и нижнем течении р. Северная Двина связаны между собой вследствие подобия синоптической обстановки. Фактор адвекции тепла становится преобладающим, если время добегания превышает 1 день.
|
|
|
