Математическая база параметриче­ской

Математическая база параметриче­ской

стандартизации

Параметры и размеры серийно вы­полняемых изделий не устанавливаются произвольно, а имеют закономерность.

Многообразие типов, параметров и размеров из­делий регламентируется параметрическими стандар­тами.

Для определения сущности параметрической стандартизации в первую очередь необходимо рассмотреть понятие параметр. Параметр продукции – это количественная характеристика ее свойств.

Наиболее важными параметрами являются характеристики, определяющие назначение продукции и условия ее использования; размерные параметры (размер одежды и обуви, вместимость посуды; весовые параметры (масса гирь); параметры, характеризующие производительность машин и приборов; энергетические параметры (мощность электродвигателя и др. ).

Набор установленных значений параметров называется параметрическим рядом. Разновидностью параметрического ряда является размерный ряд. Каждый размер изделия (материала) одного типа называется типоразмером.

Что дает параметрическая стандартизация?

Во-первых, предотвращение производства большой номенк­латуры изделий; во-вторых, создание условий для широкой унификации де­талей и узлов; в третьих, развитие предметной и подетальной специализа­ции; в четвертых, облегчение эксплуатации и ремонта изделий; в пятых, обеспечение связи между различными отраслями промыш­ленности.

Параметры и размеры серийно выпускаемых изделий устанавливаются в соответствии с системой предпочти­тельных чисел, основанной на математических методах.

Предпочтительными числаминазывают числа, которые рекомендуются выбирать как преимуществен­ные перед всеми другими при назначении величин па­раметров для вновь создаваемых изделий.

Наипростей­шие ряды предпочтительных чисел строятся на основе арифметической прогрессии.

Например:

а) возрастание с разницей 1

1-2-3-4-5-6-7…

б) возрастание с разницей 2

1-3-5-7-9-11-13…

в) убывание с разницей 0, 1

1-0, 9-0, 8-0, 7-0, 6…

Любой член арифметической прогрессии можно вычислить по формуле:

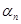,                           (3)

где  - первый член прогрессии;

 - разность прогрессии;

 - номер взятого члена.

Такие ряды предпочтительных чисел, основанные на арифметической прогрессии, используются редко, но такие стандарты есть (диаметры подшипников качения, стандарты на размеры обуви).

Достоинство такого ряда – простота. Недостаток – относительная неравномерность.

В возрастании арифметической про­грессии с разницей 1 второй член превышает первый на 100%, десятый больше девятого на 11%, а сотый больше девяносто девятого всего на 1%. Здесь большие значения следует чаще друг за дру­гом, их оказывается больше, чем маленьких, что не все­гда рационально.  

Для устранения этих недостатков используют ступенчато-арифметическую прогрессию. Такую прогрессию образуют монеты советского периода 1-2-3-5-10-15-20 копеек, где разность прогрессий составляет 1-5. Такая ступенчатая арифметическая прогрессия была принята еще в 1717 г., когда по указу Петра I устано­вили калибры ядер: 4-6-8-12-18-24-36. В настоящее время она нашла применение в стандартах на диаметры резьб, размеры болтов, винтов, шпилек и т. д.

С древних времен для построения ряда предпочти­тельных чисел использовалась геометрическая прогрес­сия, где последовательность чисел получается путем умножения предыду­щего на одно и то же число, называемое знаменателем прогрессии, который остается постоянным.

Пример:

а) возрастающая, со знаменателем 1, 5:

4-6-9-13-15-20-25…

б) убывающая со знаменателем 0, 1:

1-0, 1-0, 01-0, 001…

 Любой член геометрической прогрессии можно вычислить по формуле:

,                               (4)

где  - первый член прогрессии;

 - знаменатель прогрессии;

 - номер взятого члена.

Геометрическая прогрессия имеет ряд полезных свойств, используемых в стандартизации.

1) Относительная разность между любыми сосед­ними членами ряда постоянна;

Например, знаменатель прогрессии 2, то ряд пред­почтительных чисел

1-2-4-8-16-32-64…, где любой член прогрессии больше предыдущего на 100%.

2) Произведение или частное любых членов про­грессии является членом той же прогрессии.

Ряды предпочтительных чисел должны удовлетво­рять следующим требованиям:

1) представлять собой рациональную систему градаций, отвечающую потребностям производства и эксплуатации;

2) быть бесконечными как в сторону малых, так и в сторону больших значений;

3) включать все десятикратные значения любого члена и единицу;

4) быть простыми и легко запоминающимися.

Исследования показали, что всем этим требова­ниям удовлетворяют геометрические прогрессии с деся­тикратным увеличением каждого n-го члена.

.                                   (5)

Исходя из предыдущей формулы геометрической прогрессии, следует что , тогда знаменатель прогрессии  > 1.

Основоположником использования ряда предпоч­тительных чисел является Ш. Ренар (1886), поэтому ряд обозначается R.

ГОСТ 8032-84 составлен в соответствии с реко­мендациями международных организаций по стандартиза­ции ИСО и устанавливает четыре основных ряда пред­почтительных чисел ( ) и два дополни­тельных (  и 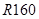), которые дополняются в отдель­ных, технически обоснованных случаях. Рассмотрим краткие сведения об этих рядах (табл. 1).

 

Таблица 1 – Ряды предпочтительных чисел

 

Условное обозначе­ние ряда	Знаменатель прогрессии	Кол-во членов ряда в десятич­ном интер­вале	Отношение разницы между смежными членами ряда, %
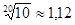
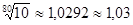
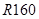
			1, 5

 

Отступления от предпочтительных чисел и их рядов до­пускаются в следующих случаях:

а) отступление от предпочтительного числа выхо­дит за пределы допускаемой погрешности (можно ис­пользовать ряд  и );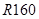

б) значения параметров технических объектов сле­дуют из закономерности, отличной от геометрической про­грессии;

Выборочные ряды предпочтительных чисел по­лучают отбором каждого 2, 3, 4… -го члена основного и дополнительного рядов, начиная с любого числа.

Например: - выборочный ряд, со­ставленный из каждого второго члена основного ряда , ограниченный членами 1 и 1000.

 - выборочный ряд, составленный из каждого третьего члена основного ряда , включая член 80 и неограниченный в обоих направлениях.

 - выборочный ряд, составленный из каждого четвертого члена основного ряда  и ограни­ченный по нижнему пределу числом 112.

 - выборочный ряд, составленный из каждого пятого члена основного ряда  и ограничен­ный по верхнему пределу членом 60.

Убывающие ряды положительных предпочти­тельных чисел получают на основе убывающей геомет­рической прогрессии, -ый член который равен

,                                   (6)

Ниже представлен пример записи убывающего ряда, , , , .

Ступенчатые ряды построены по разным геомет­рическим прогрессиям (из числа входящих в ГОСТ 8032-84).

Например: ряд 1, 0-1, 6-2, 5-4, 0-6, 3-8, 0-10, 0 состав­лен из двух рядов  со знаменателем прогрес­сии  и R10(1. 0…6. 3), имеющим

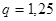
Число R определяет число членов прогрессии в од­ном десятичном интервале.

Рассмотрим пример образования предпочтитель­ных чисел ряда  в десятичном интервале от 1 до 10 (табл. 2).

Согласно ГОСТ 8032-84, установлены стандартные значения предпочтительных чисел, в диапазоне 0< а< ∞ на основе фиксированных значений предпоч­тительных чисел, включенных в десятичный интервал 1< а≤ 10.

Для перехода от предпочтительных чисел, приве­денных в таблице 2, в любой другой десятичный интер­вал нужно умножить эти числа на , где К – любое целое положительное (отрицательное) число, оп­ределяющее отдаление десятичного интервала в ту или другую сторону от заданного, принятого за нулевой.

Пример:

1) К=1 ;  

 ( )

2) К=-1 ;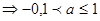

 

Таблица 2 – Ряды предпочтительных чисел

 

Номер числа	Предпочтительное число	Номер числа	Предпочтительное число
	1, 00		1, 90
	1, 06		2, 00
	1, 12		и т. д. до 40
	1, 18
	1, 25
	1, 32
	1, 40
	1, 50
	1, 60
	1, 70
	1, 80

 

3) предпочтительное число из  1, 18 необхо­димо увеличить в сторону увеличения , то 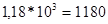. Точно так же можно определить и в сто­рону интервала уменьшения.

Из ГОСТ 8032-84 видно, что  включает все ряды предпочтительных чисел .

Задание: Проверить образование ряда предпочтительных чисел.

Составить ряд предпочтительных чисел для ряда  в виде таблицы 3.   

 

Таблица 3 - Ряд предпочтительных чисел для ряда

 

Порядковый номер	Для Предпочти­тельное число	Для Предпочти­тельное число	Для Предпочти­тельное число	Для Предпочти­тельное число
	1, 0	1, 00	1, 00
	1, 6	1, 25	1, 12
	2, 5	1, 60	1, 25
	4, 0	2, 00	1, 40
	6, 3	2, 50	1, 60
		3, 15	1, 80
		4, 00	2, 00
		5, 00	2, 24
		6, 30	2, 50
		8, 00	2, 80
			3, 15
			3, 55
			4, 00
			4, 50
			5, 00
			5, 60
			6, 30
			7, 10
			8, 00
			9, 00

 

Среди чисел есть число 3, 15, которое используется в качестве числа π =3, 14. Использование при расчетах числа π позволяет выражать предпочтительными числами длины окружностей, площади кругов, скорости резания, цилиндрические и сферические поверхности и объемы.

Если выразить диаметр окружности D предпочтительным числом и умножить это число на другое предпочтительное число 3, 15, то длина окружности l=π × D будет представлена предпочтительным числом того же ряда.

Применение системы предпочтительных чисел позволяет не только унифицировать параметры продукции определенного типа, но и увязать по параметрам продукцию различных видов – детали, изделия, транспортные средства и технологическое оборудование.

При выборе параметров необходимо руководствоваться следующим правилом: ряды деталей и узлов должны базироваться на рядах машин и оборудования, т. е. например, ряду параметров машин по R5 должен соответствовать ряд размеров деталей по R10 и т. д.

Например, в целях более эффективного использования тары для консервных банок и транспортных средств для их перевозки предлагается ряд грузоподъемности железнодорожных вагонов и автомашин, ряд размеров контейнеров, ящиков и отдельных консервных банок строить по ряду R5, тогда:

1) грузоподъемность железнодорожных вагонов – 25 т; 40 т; 63 т; 100 т.

2) грузоподъемность контейнеров – 250 кг; 400 кг; 630 кг; 1 000 кг.

3) масса ящиков – 25 кг; 40 кг; 63 кг; 100 кг.

4) масса коробок или банок – 250 г; 400 г; 630 г; 1000 г.

Таким образом, стандартизуемые и нормируемые параметры могут иметь разный характер, но при выборе их номинальных значений из рядов предпочтительных чисел значительно легче согласуются между собой изделия, предназначенные для работы в одной технологической цепочке или являющиеся объектами технологического процесса.

Вопросы для самопроверки

1. Что является теоретической базой современной стандартизации?

2. Что такое принцип предпочтительности?

3. Для чего служат предпочтительные числа?

4. Каковы правила построения рядов предпочтительных чисел по геометрической прогрессии?

4. Перечислите достоинства и недостатки рядов предпочтительных чисел основанных на арифметической прогрессии.

5. Назовите основные и дополнительные ряды предпочтительных чисел.

6. В каких случаях допускаются отступления от предпочтительных чисел и их рядов?

7. Что представляют собой выборочные ряды предпочтительных чисел?

8. Дайте определение параметрическим рядам и объясните их значимость.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: