 |
Уравнения линий на плоскости
|
|
|
|
Прямая на плоскости
Прямую на плоскости можно задать многими способами. При решении задач на прямую часто используются следующие типовые уравнения и соотношения:
1. Уравнения прямой с угловым коэффициентом 
, где k – угловой коэффициент (
, 
- угол наклона прямой к оси Ox), b – величина отрезка, отсекаемого прямой на оси Oy.
2. Уравнение прямой, проходящей через данную точку М (x 0, y 0) c данным угловым коэффициентом k
.
3. Уравнение прямой, проходящей через две данные точки M 1(x 1, y 1) и M 2(x 2, y 2)
.
Заметим, что в случае 
, уравнение принимает вид 
. Аналогично, если 
, уравнение прямой записывается 
.
4. Расстояние d от точки М 0 до прямой 
определяется по формуле
.
5. Угол j, отсчитываемый против часовой стрелки от прямой 
до прямой 
, определяется по формуле
.
Из формулы следует:
1) прямые l 1 и l 2 параллельны, если 
;
2) прямые l 1 и l 2 перпендикулярны, если 
.
6. Уравнения биссектрис углов между прямыми 
и 
имеют вид
.
7. Точка пересечения медиан делит любую из них на части в отношении 2:1 (считая от вершины).
Пример. Даны вершины треугольника А (-3,-3), В(2,7) и С (5,1). Требуется написать уравнения сторон треугольника, определить угол А треугольника, найти уравнение медианы АК и высоты АМ, сделать чертеж.
Решение. Чтобы написать уравнение стороны АВ треугольника, используем вид уравнения прямой, проходящей через две точки:
Рис. 1. Чертеж треугольника
A В: 
или у = 2х + 3.
Аналогично
АС: 
или у = 0,5 х -1,5
СВ: 
или у = -2 х + 11.
Тогда тангенс угла А определяется по формуле:
, k1=2, k2 = 0,5. Следовательно 
Ищем уравнение медианы АК. Для этого определяем координаты точки К, учитывая, что отрезок ВС в точке К делится пополам и, следовательно,
|
|
|
АК 
или 
Ищем уравнение высоты АМ, опущенного из вершины А на сторону ВС:
, где 
.
Следовательно, уравнение АМ: 
или у - 0,5х +1,5 = 0
Линии второго порядка
Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x 0, y 0) (случай В).
А В
| Окружность | 
|
| |
| Эллипс | 
|
| |
| Гипербола | 
|
| |
| Парабола | 
|  
| |
Пример 1. Пусть задано уравнение х2 + y2 - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра?
Приведем данное уравнение к виду 
. Выделим полный квадрат относительно х, прибавляя и вычитая число 4
x2 + y2 - 4x = (x2 - 4x + 4) + y2 - 4 = 0 или (x - 2)2 + y2 = 22.
х0 = 2, у0 = 0, R = 2.
Пример 2. Дано уравнение кривой второго порядка 
. Определить тип кривой, найти ее параметры и сделать чертеж.
Решение. Сравнивая с табличными данными находим, что это парабола, вершина которой находится в точке С (x 0, y 0). Приводим уравнение параболы к виду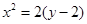 
.
х0 = 0, у0 = 2, р = 1. Чертеж
Рис. 2. Чертеж параболы
Плоскости и прямые в пространстве
Пример. Даны координаты вершин пирамиды
А 1(1,-2,-3), А 2(-3,1,1), А 3(4,3,-1), А 4(3,2,2).
Составить: 1. Уравнение плоскости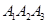 
.
2. Уравнение перпендикуляра, опущенного из вершины А 4 на грань .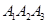
Решение. 1. Уравнение плоскости запишем, используя каноническое уравнение плоскости, проходящей через три данные точки:
.
Подставив координаты точек А 1, А 2, А 3, получим
= 
.
Разложив последний определитель по элементам первой строки, будем иметь
или
.
2. Уравнение высоты пирамиды представим в виде канонической системы уравнений прямой, проходящей через заданную точку А 4 с известным направляющим вектором 
. За направляющий вектор возьмем нормальный вектор 
плоскости 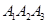, т.е. 
.
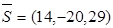Уравнение высоты: 
.
|
|
|
Примечание. Если бы в уравнении прямой один из знаменателей оказался нулевым, например
,
то уравнение прямой следовало бы записать в виде пересекающейся системы плоскостей
Наконец, если бы в уравнении прямой два знаменателя обратились в ноль, например,
,
это означало бы, что прямая является пересечением плоскостей 
и 
и ее уравнением будет система
|
|
|
