 |
Контрольная работа 1. Задания
|
|
|
|
1. Решить систему методами Крамера и последовательных исключений
| 1.1. |  .
| 1.11 |  .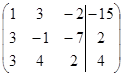
|
| 1.2 |  .
| 1.12 |  .
|
| 1.3. |  .
| 1.13 |  .
|
| 1.4. |  .
| 1.14 |  .
|
| 1.5. |  .
| 1.15 |  .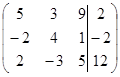
|
| 1.6. |  .
| 1.16 |  .
|
| 1.7. |  .
| 1.17 |  .
|
| 1.8. |  .
| 1.18 |  .
|
| 1.9. |  .
| 1.19 |  .
|
| 1.10 |  .
| 1.20 |  .
|
2. Даны координаты вершин пирамиды 
. Средствами векторной алгебры найти:
1) длину ребра 
;
2) угол между ребрами 
и 
;
3) уравнение плоскости 
;
4) уравнение перпендикуляра, опущенного из вершины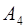 
на грань 
;
5) площадь грани ;
6) объем пирамиды.
| 2.1. |  ,
|  ,
|  ,
|  .
|
| 2.2. |  ,
|  ,
|  ,
|  .
|
| 2.3. |  ,
|  ,
|  ,
|  .
|
| 2.4. |  ,
|  ,
|  ,
|  .
|
| 2.5. |  ,
|  ,
|  ,
|  .
|
| 2.6. |  ,
|  ,
|  ,
|  .
|
| 2.7. |  ,
|  ,
|  ,
|  .
|
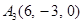| 2.8. |  ,
|  ,
|  ,
|  .
|
| 2.9. |  ,
|  ,
|  ,
|  .
|
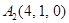| 2.10. |  ,
|  ,
|  ,
|  .
|
| 2.11. |  ,
|  ,
|  ,
|  .
|
| 2.12. |  ,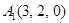
|  ,
|  ,
|  .
|
| 2.13. |  ,
|  ,
|  ,
|  .
|
| 2.14. |  ,
|  ,
|  ,
|  .
|
| 2.15. |  ,
|  ,
|  ,
|  .
|
| 2.16. |  ,
|  ,
|  ,
|  .
|
| 2.17. |  ,
|  ,
|  ,
|  .
|
| 2.18. |  ,
|  ,
|  ,
|  .
|
| 2.19. |  ,
|  ,
|  ,
|  .
|
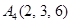| 2.20. |  ,
|  ,
|  ,
|  .
|
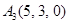3. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж треугольника.
| № | А | В | С | № | А | В | С |
| 3.1. | (-5, 3) | (1,6) | (5, 1) | 3.11 | (1, 5) | (4, 0) | (-5,-4) |
| 3.2. | (-7, 1) | (5, 0) | (2, 5) | 3.12 | (4, 2) | (2, 0) | (-1, 2) |
| 3.3. | (5, 1) | (0, 4) | (-2, 2) | 3.13 | (0, -2) | (-2, 1) | (3, 4) |
| 3.4. | (5, 2) | (-1, 0) | (3, 4) | 3.14 | (-1, 2) | (1, 1) | (-5, 3) |
| 3.5. | (2, -2) | (3, -4) | (2, -1) | 3.15 | (4, 2) | (-3, 3) | (2, -1) |
| 3.6. | (1, 0) | (2, 5) | (-1, 1) | 3.16 | (4, 4) | (5, 1) | (-1, 0) |
| 3.7. | (0, -3) | 
| (-2, -1) | 3.17 | (-2, 4) | (5, 1) | (0, -3) |
| 3.8. | (-2, 1) | (3, 1) | (0, -2) | 3.18 |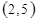 
| (-1, 1) | (0,3) |
| 3.9. | (-3, 3) | (7, 5) | (4, 1) | 3.19 | (1, 5) | (-5, 3) | (1,3) |
| 3.10 | (2, 0) | (5, -2) | (8, 2) | 3.20 | 
| (-2,1) | (0, -3) |
4.Указать тип кривой второго порядка, найти ее параметры и сделать чертеж.
4.1.  .
| 4.11. 
|
4.2. 
| 4.12. 
|
4.3. 
| 4.13. 
|
4.4. 
| 4.14. 
|
4.5. 
| 4.15. 
|
4.6. 
| 4.16. 
|
4.7. 
| 4.17. 
|
4.8. 
| 4.18.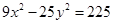 
|
4.9. 
| 4.19. 
|
4.10. 
| 4.20. 
|
Контрольная работа 2
Введение в математический анализ. Функция и ее свойства
Пример 1. Найти область определения функции D (f)
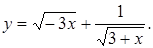
Решение. Если числовая функция задана аналитически (в виде формулы 
) и область ее определения не указана, то считают, что эта область есть множество всех действительных значений аргумента, при которых выражение 
- действительное число. Для существования заданной функции 
необходимо, чтобы имело место неравенство 
. Для существования функции 
должно иметь место неравенство 
, откуда 
. Область определения исходной функции 
или 
.
|
|
|
Пример 2. Найти область определения функций:
Решение. Для приведенных выше функций области определения удовлетворяют условиям: 1. 
2. 
3. 
4. 
5. 
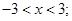6. 
Следовательно,
; 
;
; 
;
; 
.
Пример 3. Найти область определения функции
.
Решение. Для существования функции 
необходимо, чтобы 
. Для существования функции 
надо, чтобы 
, откуда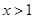 
. Для существования функции 
необходимо, чтобы 
, откуда и 
.
Таким образом, получены условия
.
Пример 4. Найти область определения функции 
Решение. Так как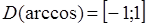 
, то 
. Решив неравенство, найдем область определения функции
Применим метод интервалов (рис. 3)
1. 
2. 
Рис. 3
Система неравенств имеет решение 
. Следовательно, 
.
Пример 5. Определить, являются ли функции
1. 
; 2. 
;
3. 
; 4.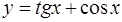 
четными или нечетными.
Решение. Для определения свойств четности или нечетности функции следует проверить выполнение следующих положений:
1. Является ли область определение симметричной относительно начала координат, т.е. если 
, то и 
;
2. Выполняются ли равенства 
или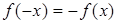 
. При выполнении первого равенства функция окажется четной с графиком, симметричным относительно оси ординат, во втором – нечетной с графиком, симметричным относительно начала координат.
Для указанных в задаче функций:
1. 
,
то функция 
- нечетная;
2. 
,
то функция 
является четной;
3. 
,
следовательно, функция нечетная;
4. 
,
следовательно, функция 
не является ни четной, ни нечетной.
Пример 6. Найти период функции
|
|
|
.
Решение. При решении задач на нахождение периода функции следует использовать следующее.
Функция является периодической, если существует такое число Т ¹0, что при любом x из области определения функции числа 
и 
также принадлежат этой области и выполняется равенство 
.
В этом случае Т есть период функции .
Так как 
, то период Т =1.
|
|
|
