Свойства дифференцируемых функций

Пример. Найти пределы используя правило Лопиталя.

1. ; 2. ; 3. ; 4. .

Решение. Убедившись, что имеет место неопределенность  или 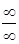, применяем затем правило Лопиталя.

1.

;

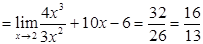2.

;

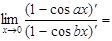
здесь правило Лопиталя применено дважды.

3.

;

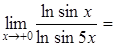
4. .

 Исследование поведения функций

Пример 1. Исследовать и построить график функции

.

Решение.  

1. Заданная функция определена и непрерывна на всей числовой оси

.

2. Функция нечетная, ибо , ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для .

3. График функции пересекается с осями координат только в начале координат, так как .

4. Исследуем функцию  на наличие асимптот:

а) вертикальных асимптот график функции не имеет;

б) невертикальная асимптота имеет уравнение .

,

.

Таким образом, уравнение асимптоты .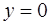

5. Исследуем функцию на экстремум

.

 нигде не обращается в нуль;  не существует в точках , которые являются критическими.

Исследуем знак производной на интервале [0; ∞) (рис.5)

 

                                   0             1                   

      

Рис. 5

 есть точка максимума, .

6. Исследуем график функции на выпуклость и вогнутость

.

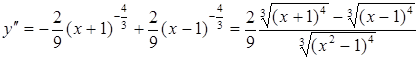в точке ; не существует в точках 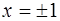. Эти точки могут быть абсциссами точек перегиба. Исследуем знак второй производной на интервале [0; ∞) (рис.6)

   

                          

                                             0                   1

 

Рис. 6

 не является точкой перегиба.

Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на  интервале (- ∞; 0) (рис.7)    

      

                        

Рис. 7

Пример 2. Найти наибольшее и наименьшее значения функции 

на отрезке [-4; 4].

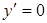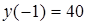Решение. 1. Найдем критические точки функции , лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках: ;   в точках  и . Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:  и .

2. Вычислим значения функции на концах отрезка [-4; 4]:  и .

3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции  на отрезке [-4; 4]  равно 40 и достигается ею во внутренней критической точке , а ее наименьшее значение равно -41 и достигается на левой границе отрезка .

Во многих геометрических, физических и технических задачах требуется найти наибольшее или наименьшее значение величины, связанной функциональной зависимостью с другой величиной.

Для решения такой задачи следует, исходя из ее условия, выбрать независимую переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.

 

     Контрольная работа 2. Задания

 

1. Найти указанные пределы. В пунктах а, б не пользуясь правилом Лопиталя, в пункте в по правилу Лопиталя. При решении примера (б) используйте формулы тригонометрии.

	а	б	в
1.1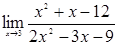
1.2
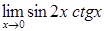
1.3
1.4
1.5
1.6
1.7
1.8
1.9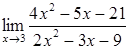
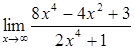
1.10
1.11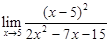
1.12.
1.13
1.14
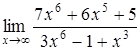
1.15
1.16
1.17
1.18
1.19
1.20.

 

1. Найти точки разрыва функции, если они существуют. Сделать чертеж 

2.1	2.11.
2.2.	2.12.
2.3.	2.13.
2.4.	2.14.
2.5.	2.15.
2.6.	2.16.
2.7.	2.17.
2.8.	2.18.
2.9.	2.19.
2.10.	2.20.

 

2. Найти производные   данных функций

№	а	б	в	г
3.1
3.2
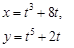
3.3
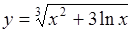
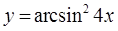
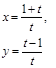
3.4
3.5
3.6
3.7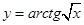
3.8
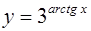
3.9
3.10
3.11
3.12
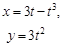
3.13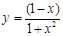
3.14
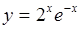
3.15
3.16
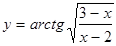
3.17
3.18
3.19
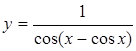
3.20

                                                          

3. Найти интервалы монотонности и экстремумы функции.

4.1. ;	4.11. ;
4.2. ;	4.12. ;
4.3. ;	4.13. ;
4.4. ;	4.14. ;
4.5. 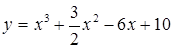;	4.15. ;
4.6. ;	4.16. ;
4.7. ;	4.17. ;
4.8. ;	4.18. ;
4.9. ;	4.19. ;
4.10. ;	4.20. ;

 

Библиографический список

а) основная учебная литература

1. Письменный Д. Т. Конспект лекций по высшей математике. Т. 1 – 2. М.: АЙРИС ПРЕСС, 2011.

2. Письменный Д. Т. Сборник задач по высшей математике. 1–й курс. – М.: АЙРИС ПРЕСС, 2008.

3. Минорский В. П. Сборник задач по высшей математике. – М.: ФИЗМАТЛИТ, 2009.

б) дополнительная литература

4. Высшая математика в упражнениях и задачах. Т. 1, 2. Д. Е. Данко и др. – М.: ОНИКС 21век, 2003.

5. Беклемешев Д. В. Курс аналитической геометрии и линейной алгебры. – М.: ФИЗМАТЛИТ, 2005.

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: