 |
Формула аффинного преобразования
|
|
|
|
Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Аффинные преобразования евклидовой плоскости в сопряжённых комплексных координатах
Выполнила:
студентка V курса
математического факультета
Куршакова О.В.
__________________
Научный руководитель:
кандидат физ.-мат. наук,
профессор кафедры алгебры и геометрии
Понарин Я.П.
__________________
Рецензент:
ст. преподаватель кафедры алгебры и геометрии
Суворов А.Н.
__________________
Допущена к защите в ГАК
Зав. кафедрой ________________ Вечтомов Е.М.
«» _______________
Декан факультета ______________ Варанкина В.И.
«»_______________
Киров 2005
Оглавление
Предисловие. 2
Глава i. Теория аффинных преобразований в сопряжённых комплексных координатах.. 3
§1. Определение и формула аффинного преобразования в сопряжённых комплексных координатах. 3
1.1. Определение аффинного преобразования. 3
1.2. Формула аффинного преобразования. 3
§2. Уравнение образа прямой при аффинном преобразовании. 4
§ 3. Формула обратного преобразования. 5
§ 4. Основная теорема теории аффинных преобразований. 6
§5. Свойство площадей треугольников. 7
§6. Род аффинного преобразования. 8
6.1. Ориентация плоских фигур. 8
6.2. Ориентация пар векторов. 8
§7. Неподвижные точки и двойные прямые аффинных преобразований. 10
7.1. Неподвижные точки аффинных преобразований. 10
7.2. Двойные прямые аффинных преобразований. 12
|
|
|
глава ii. Частные виды аффинных преобразований в сопряжённых комплексных координатах.. 15
§1. Преобразование подобия. 15
§2. Преобразование родства. 16
2.1. Понятие преобразования родства. 16
2.2. Сжатие и его частные виды.. 18
2.3. Сдвиг. 19
§3. Эллиптический поворот. 21
§4. Параболический поворот. 24
§5. Представление аффинных преобразований композициями их частных видов. 25
Библиографический список. 28
Предисловие
Целью данной работы является рассмотрение и изучение аффинных преобразований евклидовой плоскости в сопряжённых комплексных координатах.
Теория аффинных преобразований впервые была рассмотрена Дарбу. В данной работе эта теория изложена методом комплексных чисел.
В работе рассмотрена общая теория для всех аффинных преобразований евклидовой плоскости в сопряжённых комплексных координатах, а также такие частные виды аффинных преобразований, как подобие, родство, эллиптический поворот, параболический поворот. Первое из них имеет две разновидности – подобия первого и второго рода, и теория для него разработана Скопецом З.А. совместно с Понариным Я.П. Родство – аффинное преобразование, имеющее прямую неподвижных точек, у которого есть частные виды, также рассмотренные в работе. Теория этого аффинного преобразования для комплексных чисел разработана Понариным Я.П. Эллиптический и параболический повороты – это эквиаффинные преобразования, являющиеся композицией других аффинных преобразований. Они также определены научным руководителем.
Для каждого из четырёх рассмотренных аффинных преобразований и частных видов некоторых из них получены координатные формулы в сопряжённых комплексных координатах, изучены их простейшие свойства.
Глава I. Теория аффинных преобразований в сопряжённых комплексных координатах
Определение и формула аффинного преобразования в сопряжённых комплексных координатах
|
|
|
Определение аффинного преобразования
Введём определение аффинного преобразования евклидовой плоскости в сопряжённых комплексных координатах.
Преобразование евклидовой плоскости называется аффинным, если оно отображает каждую прямую на прямую. [1]
Формула аффинного преобразования
Мы хотим построить теорию аффинных преобразований с помощью комплексных чисел. Но для этого нужно иметь формулу аффинного преобразования, то есть выражение комплексной координаты z ’ образа данной точки M (z) через координату z этой точки М.
Известно, что аффинное преобразование плоскости в аффинных (и в частности, в прямоугольных декартовых) координатах имеет формулы:
где 
(1)
Так как хотим получить формулу аффинного преобразования в сопряжённых комплексных координатах, то нужно получить выражение комплексной координаты z ’= x ’+ iy ’ точки M ’(z ’) через комплексную координату её образа z = x + iy точки M (z): в выражение z’ подставим вместо x’ и y’ их выражения из формул (1): 
, раскрыв скобки и приведя подобные слагаемые в правой части этого равенства, получим 
. Теперь произведём тождественное преобразование над коэффициентами при x и iy:
Сгруппировав коэффициенты при x и iy, получаем следующее:
. Введя обозначения 
, 
, 
и учитывая, что 
и 
, имеем выражение комплексной координаты z ’ точки M ’ через комплексную координату её образа z точки M: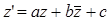 
. Осталось найти определитель этого преобразования. После некоторых преобразований определитель примет вид: 
, откуда, воспользовавшись введёнными обозначениями коэффициентов аффинного преобразования, имеем: 
. Таким образом, формула аффинного преобразования в сопряжённых комплексных координатах имеет вид:
, где 
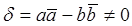(2)
|
|
|
