 |
Двойные прямые аффинных преобразований
|
|
|
|
Найдём условие, при котором прямая при аффинном преобразовании (2) перейдёт сама в себя, то есть будет являться инвариантом аффинного преобразования.
 Возьмём уравнение прямой (3), которая при аффинном преобразовании перейдёт в прямую
Возьмём уравнение прямой (3), которая при аффинном преобразовании перейдёт в прямую 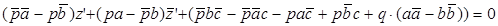 . Для того, чтобы прямая (3) перешла сама в себя, необходимо выполнение следующих условий:
. Для того, чтобы прямая (3) перешла сама в себя, необходимо выполнение следующих условий: 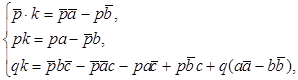 где
где  R. (14) Преобразуем первые два равенства системы (14) к виду
R. (14) Преобразуем первые два равенства системы (14) к виду 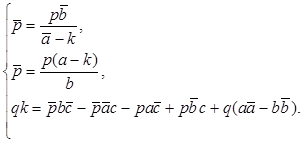 Приравняем теперь первые два равенства и после преобразования получим:
Приравняем теперь первые два равенства и после преобразования получим: 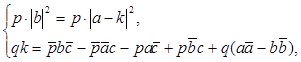 представим первое равенство системы в виде совокупности двух условий
представим первое равенство системы в виде совокупности двух условий 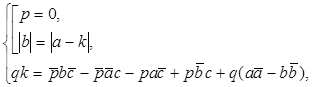 теперь эту систему можно представить как совокупность двух систем
теперь эту систему можно представить как совокупность двух систем  (15) Рассмотрим каждую систему полученной совокупности отдельно.
(15) Рассмотрим каждую систему полученной совокупности отдельно.
1) Первая система совокупности приводится к виду 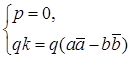 и теперь уже она может быть представлена в виде совокупности двух систем
и теперь уже она может быть представлена в виде совокупности двух систем 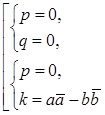 Отметим, что если для прямой (3) выполняется первая система, то нет и самой прямой (3). Решая вторую систему, также получим, что нет самой прямой (оба коэффициента равны нулю). Таким образом получили, что первая система совокупности (15) не имеет решений.
Отметим, что если для прямой (3) выполняется первая система, то нет и самой прямой (3). Решая вторую систему, также получим, что нет самой прямой (оба коэффициента равны нулю). Таким образом получили, что первая система совокупности (15) не имеет решений.
2) Рассмотрим вторую систему совокупности (15) 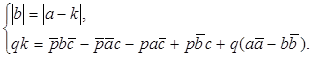 . Выразим из второго равенства системы коэффициент q и воспользуемся тем, что
. Выразим из второго равенства системы коэффициент q и воспользуемся тем, что 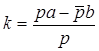 (из второго равенства (14)), тогда рассматриваемая система будет выглядеть следующим образом:
(из второго равенства (14)), тогда рассматриваемая система будет выглядеть следующим образом:
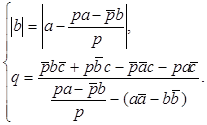 (16)
(16)
Преобразуем отдельно каждое равенство системы (16).
А) Первое равенство системы после некоторых преобразований примет вид 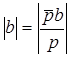 , откуда
, откуда 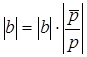 и выполнение этого условия является очевидным, следовательно, первое равенство системы (16) ничего существенного нам не давало.
и выполнение этого условия является очевидным, следовательно, первое равенство системы (16) ничего существенного нам не давало.
Б) Рассмотрим теперь второе равенство, преобразуем его правую часть 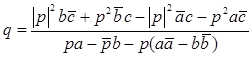 , тогда полученное соотношение на коэффициенты прямой (2):
, тогда полученное соотношение на коэффициенты прямой (2): 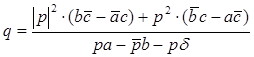 (17) является условием того, что прямая (3) - двойная прямая аффинного преобразования (2).
(17) является условием того, что прямая (3) - двойная прямая аффинного преобразования (2).
|
|
|
Докажем, что если для коэффициентов прямой (3) p и q верно равенство (17), то она является двойной прямой аффинного преобразования с коэффициентами a, b, c и определителем  .Возьмём прямую
.Возьмём прямую 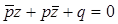 . При аффинном преобразовании с коэффициентами a, b, c она перейдёт на прямую
. При аффинном преобразовании с коэффициентами a, b, c она перейдёт на прямую 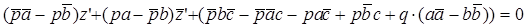 . Покажем, что будут выполняться равенства
. Покажем, что будут выполняться равенства 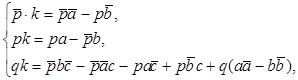 где k – коэффициент пропорциональности. Найдём k из последнего равенства системы
где k – коэффициент пропорциональности. Найдём k из последнего равенства системы  . Подставим вместо q его выражение через коэффициенты аффинного преобразования и коэффициент р, упростим выражение и получим
. Подставим вместо q его выражение через коэффициенты аффинного преобразования и коэффициент р, упростим выражение и получим 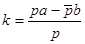 . Очевидно, что при таком k верны и два первых уравнения системы, следовательно, прямая является двойной, что и требовалось доказать.
. Очевидно, что при таком k верны и два первых уравнения системы, следовательно, прямая является двойной, что и требовалось доказать.
Глава II. Частные виды аффинных преобразований в сопряжённых комплексных координатах
Преобразование подобия
Преобразованием подобия (или подобием) называется преобразование, которое каждые две точки P и Q отображает в такие две точки P ’ и Q ’, что P ’ Q ’= k · PQ, где k - постоянное действительное положительное число, называемое коэффициентом подобия. [2]
Введём в рассмотрение аффинное преобразование (2). Рассмотрим неколлинеарные точки M (z), P (p), Q (q) и их образы M ’(z ’), P ’(p ’), Q ’(q ’) при некотором аффинном преобразовании (2). Преобразование подобия задаётся тремя парами точек M " M ’, P " P ’, Q " Q ’ так, что треугольник M ’ P ’ Q ’ подобен треугольнику MPQ.
Существует два рода преобразований подобия. Подобие первого рода сохраняет ориентацию каждого отображаемого треугольника, а подобие второго рода отображает каждый треугольник в треугольник, противоположно ориентированный с ним. Рассмотрим теперь подобие каждого рода отдельно.
I. Пусть MPQ и M ’ P ’ Q ’ – одинаково ориентированные подобные треугольники, тогда выполняются равенства  , где
, где 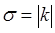 .
.
|
|
|
Рассмотрим равенство 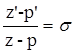 , откуда
, откуда  , тогда
, тогда 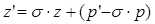 . Обозначим второе слагаемое как
. Обозначим второе слагаемое как  , получим равенство, задающее преобразование подобия первого рода:
, получим равенство, задающее преобразование подобия первого рода:
 , где
, где  . (18)
. (18)
II. Рассмотрим теперь подобные и противоположно ориентированные треугольники MPQ и M ’ P ’ Q ’. Для них верны равенства: 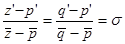 , где
, где 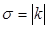 . Рассмотрим равенство
. Рассмотрим равенство 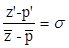 , преобразуем его к виду
, преобразуем его к виду  , тогда можем выразить z ’:
, тогда можем выразить z ’:  , обозначим второе слагаемое за ρ, тогда получим равенство, которым задаётся преобразование подобия второго рода
, обозначим второе слагаемое за ρ, тогда получим равенство, которым задаётся преобразование подобия второго рода 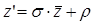 , где
, где  (19)
(19)
Преобразование родства
|
|
|


