 |
Понятие преобразования родства
|
|
|
|
Родство – аффинное преобразование, имеющее прямую неподвижных точек. Его задаёт формула:
 , где
, где  ,
,  ,
,  (20)
(20)
Осью этого преобразования является прямая  , примем её за действительную ось Ох:
, примем её за действительную ось Ох:  [1]. Тогда очевидно, что с=0 и b =1- a. Поэтому преобразование (20) с действительной осью записывается формулой:
[1]. Тогда очевидно, что с=0 и b =1- a. Поэтому преобразование (20) с действительной осью записывается формулой:
 , где
, где 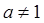 (21)
(21)
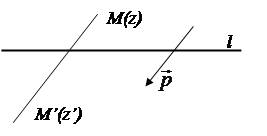 |
Рис. 2
Выясним особенности этого преобразования. Перепишем его следующим образом  (22) составим из этого выражения и сопряжённого к нему выражения пропорцию
(22) составим из этого выражения и сопряжённого к нему выражения пропорцию  . Откуда
. Откуда 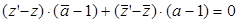 , а это является условием того, что векторы с координатами
, а это является условием того, что векторы с координатами  и
и  перпендикулярны. Так как а-1 – постоянные вектор, а z и z ’ – координаты соответственных точек М и М’ при аффинном преобразовании (рис. 2), то все прямые, соединяющие точки М и М’ будут параллельны между собой и параллельны некоторому вектору
перпендикулярны. Так как а-1 – постоянные вектор, а z и z ’ – координаты соответственных точек М и М’ при аффинном преобразовании (рис. 2), то все прямые, соединяющие точки М и М’ будут параллельны между собой и параллельны некоторому вектору  с координатой (а-1) i, называемому направлением аффинного преобразования, в данном случае – родства.
с координатой (а-1) i, называемому направлением аффинного преобразования, в данном случае – родства.
Если (а-1) – чисто мнимое число (то есть  , откуда
, откуда  ), то направление родства будет коллинеарно оси родства. В этом случае аффинное преобразование называется сдвигом вдоль прямой и условия, которые его задают, имеют вид
), то направление родства будет коллинеарно оси родства. В этом случае аффинное преобразование называется сдвигом вдоль прямой и условия, которые его задают, имеют вид  ,
,  ,
,  (23)
(23)
Если же направление аффинного преобразования не совпадает с направлением его оси, то оно называется сжатием к прямой и его задают следующие условия:  ,
,  ,
, 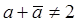 (24)
(24)
|
|
|
Сжатие и его частные виды
Найдём собственные числа λ преобразования сжатия (24) из условия  . Составим систему из этого условия и сопряжённого к нему выражения:
. Составим систему из этого условия и сопряжённого к нему выражения:  . Чтобы найти собственные числа, нужно решить уравнение
. Чтобы найти собственные числа, нужно решить уравнение  , откуда получим
, откуда получим  и
и  .
.
Примем без доказательства следующую теорему [1]: если λ – собственное действительное число аффинного преобразования, то множество точек, каждая из которых делит в отношении  отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.
отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.
 |
Рис. 3
Очевидно, что прямые MM ’ и NN ’ (рис. 3) являются двойными прямыми и λ2 – действительное число, то точка Р делит отрезок MM ’ в отношении 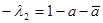 , то есть
, то есть  . Число
. Число  = δ называется коэффициентом сжатия. Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием.
= δ называется коэффициентом сжатия. Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием.
Рассмотрим частный случай сжатия – косую симметрию [1]. Это инволютивное преобразование, то есть оно тождественно преобразованию, обратному ему. Преобразование, обратное (24), имеет формулу:
 (25)
(25)
Оно имеет ту же ось, что и (24). Равенство преобразований (24) и (25) имеет место тогда и только тогда, когда  , откуда
, откуда  , то есть а – чисто мнимое число. Таким образом, формулой (24) при условии
, то есть а – чисто мнимое число. Таким образом, формулой (24) при условии  задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен
задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен  , следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.
, следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.
Если а=0, получаем осевую симметрию относительно действительной оси. Осевая симметрия – аффинное преобразование также второго рода (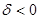 ).
).
Сдвиг
|
|
|
Выясним, как перемещается по плоскости точка при сдвиге (рис.4). Рассмотрим равенство (22), возьмём модули обеих частей этого равенства
 (26)
(26)
и посмотрим, чем является каждый модуль в (26).
 |
Рис. 4
 - это расстояние от точки М(z) до её образа M ’(z ’) при аффинном преобразовании.
- это расстояние от точки М(z) до её образа M ’(z ’) при аффинном преобразовании. 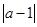 - это модуль постоянного вектора, перпендикулярного направлению сдвига, а
- это модуль постоянного вектора, перпендикулярного направлению сдвига, а  - это расстояние от М(z) до точки с координатой, сопряжённой z, равное удвоенному расстоянию от точки M (z) до действительной оси Ох.
- это расстояние от М(z) до точки с координатой, сопряжённой z, равное удвоенному расстоянию от точки M (z) до действительной оси Ох.
Преобразуем правую часть (26): 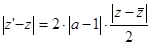 , (27) тогда из (22) и (27) следует, что при сдвиге каждая точка M (z) смещается параллельно его оси на расстояние
, (27) тогда из (22) и (27) следует, что при сдвиге каждая точка M (z) смещается параллельно его оси на расстояние  , пропорциональное расстоянию
, пропорциональное расстоянию  от этой точки до действительной оси. Коэффициент пропорциональности этих расстояний
от этой точки до действительной оси. Коэффициент пропорциональности этих расстояний  называется коэффициентом сдвига.
называется коэффициентом сдвига.
Найдём собственные числа преобразования сдвига из уравнения, составленного аналогично тому, как составляли для сжатия:  , откуда найдём
, откуда найдём 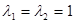 . Значит, преобразование сдвига имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
. Значит, преобразование сдвига имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
Определитель преобразования сдвига  строго больше нуля, поэтому сдвиг – аффинное преобразование первого рода.
строго больше нуля, поэтому сдвиг – аффинное преобразование первого рода.
Эллиптический поворот
Эллипс – это образ окружности при аффинном преобразовании. [1]
Рассмотрим ортогональное сжатие g к действительной оси.
Его задают условия:  (28)
(28)
а обратное к нему аффинное преобразование g-1 имеет формулу:  , где
, где  , откуда в силу (28) обратное преобразование имеет вид:
, откуда в силу (28) обратное преобразование имеет вид:  (29)
(29)
При ортогональном сжатии окружность  перейдёт в эллипс (рис. 5). Коэффициент рассматриваемого сжатия равен
перейдёт в эллипс (рис. 5). Коэффициент рассматриваемого сжатия равен  , тогда
, тогда 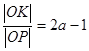 .
.  и
и  называются большой и малой осями эллипса при
называются большой и малой осями эллипса при 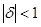 . Найдём уравнение этого эллипса. Для этого в уравнении окружности заменим z на правую часть (29), получим:
. Найдём уравнение этого эллипса. Для этого в уравнении окружности заменим z на правую часть (29), получим:  , тогда
, тогда  . Преобразовав данное равенство, получим:
. Преобразовав данное равенство, получим:  , откуда получаем уравнение эллипса
, откуда получаем уравнение эллипса  .
.
|
|
|
Рассмотрим две произвольные точки окружности N и N 1. Точку N можно перевести в точку N 1 поворотом h на некоторый угол  вокруг точки О:
вокруг точки О:  , где
, где  ,
,  ,
,  .
.

Y
P N1
N
M
K M1
C O D X
Т
Q
Рис. 5
Пусть точки М и М1 – образы точек соответственно N и N 1 при ортогональном сжатии g. Тогда точку М можем перевести в точку М1 следующим образом:
1)  (преобразование, обратное ортогональному сжатию);
(преобразование, обратное ортогональному сжатию);
2)  (поворот вокруг точки О на угол
(поворот вокруг точки О на угол  );
);
3)  (ортогональное сжатие).
(ортогональное сжатие).
Тогда  , где
, где 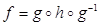 . Найдём формулу преобразования f.
. Найдём формулу преобразования f.
1. Сначала найдём формулу преобразования  :
:  .
.
2. Найдём формулу для преобразования f:  , откуда получаем
, откуда получаем  - это формула эллиптического поворота.
- это формула эллиптического поворота.
Проверим, будет ли определитель рассматриваемого преобразования не равен нулю. Преобразуем выражение определителя
 , используя равенство
, используя равенство  , тогда получим, что
, тогда получим, что  . Следовательно, определитель преобразования не равен нулю, и f является аффинным преобразованием, что и требовалось доказать.
. Следовательно, определитель преобразования не равен нулю, и f является аффинным преобразованием, что и требовалось доказать.
Так как определитель рассматриваемого аффинного преобразования положителен, то эллиптический поворот – это аффинное преобразование первого рода.
Это преобразование имеет единственную неподвижную точку О, значит оно является центроаффинным. При этом преобразовании каждая точка М плоскости (М ≠ О) переходит в другую точку, которая принадлежит соответствующему эллипсу. Этот эллипс при рассмотренном преобразовании переходит сам в себя. Преобразование с объявленными свойствами называется эллиптическим поворотом.
|
|
|
Выясним, имеет ли эллиптический поворот инвариантные пучки параллельных прямых. Для этого найдём дискриминант характеристического уравнения этого преобразования. Комплексные координаты векторов  при аффинном преобразовании (2) переходят в коллинеарные им векторы
при аффинном преобразовании (2) переходят в коллинеарные им векторы  по формуле
по формуле 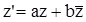 , откуда получаем уравнение
, откуда получаем уравнение  . Решая его, получим характеристическое уравнение
. Решая его, получим характеристическое уравнение  . Найдём (
. Найдём (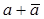 ), его значение равно
), его значение равно  , тогда характеристическое уравнение запишется в виде:
, тогда характеристическое уравнение запишется в виде:  . Его дискриминант
. Его дискриминант  отрицателен (так как
отрицателен (так как  ). Следовательно, f – аффинное преобразование с единственной неподвижной точкой О и не имеющее инвариантных пучков параллельных прямых, то есть эллиптический поворот – эквицентроаффинное преобразование.
). Следовательно, f – аффинное преобразование с единственной неподвижной точкой О и не имеющее инвариантных пучков параллельных прямых, то есть эллиптический поворот – эквицентроаффинное преобразование.
Формулу (29) эллиптического поворота можно записать в виде системы условий:  Эту формулу можно представить иначе:
Эту формулу можно представить иначе:  , то есть эллиптический поворот является композицией сжатия к действительной оси
, то есть эллиптический поворот является композицией сжатия к действительной оси  и подобия первого рода
и подобия первого рода  с центром в точке О.
с центром в точке О.
§4. Параболический поворот
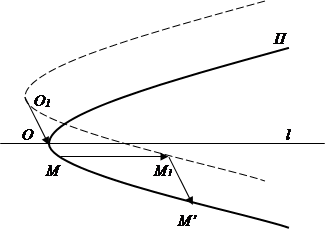
Покажем, что параболу можно перевести в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига. Пусть М – произвольная точка параболы П с осью l (рис. 6), примем эту ось за действительную. Произведём сдвиг с этой же осью l: 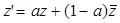 , где
, где  ,
, 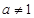 . Этот сдвиг переведёт точку М в точку М1 и параболу П – в параболу П1. Параболы П и П1 равны с точностью до сдвига.
. Этот сдвиг переведёт точку М в точку М1 и параболу П – в параболу П1. Параболы П и П1 равны с точностью до сдвига.
|
Рис. 6
Теперь произведём параллельный перенос параболы П1:  (
( ), где
), где 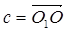 . Тем самым, парабола П 1 перейдёт в параболу П, а точка М1 перейдёт в точку М’ параболы П.
. Тем самым, парабола П 1 перейдёт в параболу П, а точка М1 перейдёт в точку М’ параболы П.
Таким образом получили, что парабола переходит в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига [1,3]. Это преобразование называется параболическим поворотом и имеет формулу  , где
, где  ,
, 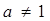 ,
,  (30)
(30)
Определитель найденного преобразования  . Так как определитель отличен от нуля, параболический поворот является аффинным преобразованием, а так как он больше нуля, - аффинным преобразованием первого рода.
. Так как определитель отличен от нуля, параболический поворот является аффинным преобразованием, а так как он больше нуля, - аффинным преобразованием первого рода.
Найдём собственные числа параболического поворота аналогично тому, как делали это для других рассмотренных аффинных преобразований. Найдём собственные числа λ из условия  . В процессе нахождения приходим к характеристическому уравнению
. В процессе нахождения приходим к характеристическому уравнению  , но так как
, но так как  , характеристическое уравнение примет вид
, характеристическое уравнение примет вид  , откуда
, откуда 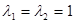 . Следовательно параболический поворот имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
. Следовательно параболический поворот имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
|
|
|
|
|
|


