 |
П.1. Постановка задачи динамического программирования
|
|
|
|
Динамическим программированием (ДП) называется раздел математического программирования, посвященный исследованию многошаговых задач принятия оптимальных решений.
Одним из основателей ДП считают американского математика Ричарда Эрнеста Беллмана (1920 – 1984 гг.). В 1951 г. в работе «Динамическое программирование» он изложил основные принципы новой теории.
Методы динамического программирования могут применяться к разнообразным задачам планирования и управления, а также к задачам чисто технического содержания (трассирование дорог, формирование каскада ГЭС и т.д.). Помимо этого ДП стало важным инструментом для анализа моделей исследования операций, таких как управление запасами, замена оборудования, финансирование предприятий и т.п. Вообще считается, что ДП приспособлено, в отличие от ЛП, к решению сравнительно небольших по масштабу экономических задач.
Как уже говорилось, ДП занимается многошаговыми задачами. Некоторые задачи разбиваются на шаги естественно (последовательность тестов по определению качества продукта, последовательность отделения ступеней ракеты и т.д.), в некоторых разбиение на шаги вводится искусственно, исходя из соображений удобства (прокладка трассы между двумя пунктами, наведение ракеты на цель, поквартальное планирование финансирования).
Приведем общую постановку задачи ДП.
Пусть имеется некоторая система S. В результате управления система из состояния S0 переходят в некоторое состояние Sn. Разобьем процесс управления системой на n шагов. Таким образом, управление системой становится пошаговым. На каждом шаге k система дает прибыль, которую мы обозначим через wk. Пусть общая прибыль W(S) за все время управления складывается из прибылей, полученных на каждом этапе
|
|
|
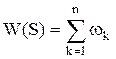 .
.
Общая прибыль в этом случае – критерий правильности выбора управления на n шагах.
Такое свойство критерия эффективности W называют аддитивностью критерия.
Обозначим через xk управление на k-том шаге. Естественно, что в корректно поставленных задачах на решения накладываются некоторые ограничения (xk Î Dk). Решение xk может быть как числом, так и вектором, функцией, качественным признаком и т.д.
Совокупность пошаговых управлений Х(x1, x2, …, xn) назовем политикой. Политика Х за n шагов приводит систему S из состояния S0 в состояние Sn (см. рис. 1.1).
     Х1 Х2 Хn Х1 Х2 Хn
     S0 S1 S2... Sn – 1 Sn S0 S1 S2... Sn – 1 Sn
|
Рис. 1.1.
Требуется найти такую политику, при которой прибыль W максимальная:
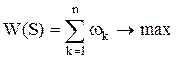 .
.
Политику, при которой достигается максимум прибыли, называют оптимальной.
Любую многошаговую задачу можно решать двумя способами. Первый – можно попробовать отыскать оптимальную политику Х целиком. Второй – искать оптимальную политику пошагово, на каждом этапе оптимизируя только один шаг.
Как правило, второй подход проще. Однако в этом случае исследователя подстерегает один неприятный момент. Оптимизируя решение на некотором шаге, сложно предугадать, как оно отразится в дальнейшем на работе системы. Оптимальное решение, принятое на отдельном этапе, может повредить итоговой прибыли, как это случилось с конькобежцем из песни В.Высоцкого:
Воля волей, если сил невпроворот,
А я увлекся,
Десять тысяч я рванул, как на пятьсот,
И спекся.
Пусть, например, планируется финансирование ряда предприятий на несколько лет. Причем одно предприятие нефтедобывающее, другое - производит оборудование для нефтедобычи, третье – разрабатывает новые технологии для более эффективной нефтедобычи. Естественно, что из трех предприятий нефтедобывающее наиболее прибыльно. Однако, вкладывать деньги только в него недальновидно, поскольку со временем оборудование начнет выходить из строя, а заменить его будет нечем. Если не внедрять новые технологии, то конкуренты вытеснят фирму с рынка, и ее доходы со временем непременно снизятся.
|
|
|
Все сказанное свидетельствует о том, что, принимая решение на некотором этапе, следует думать о последствиях. Это утверждает основополагающий принцип ДП – принцип Беллмана.
Принцип Беллмана. Каково бы ни было состояние системы S в результате какого-либо числа шагов, на ближайшем шаге нужно выбрать управление так, чтобы прибыль на данном шаге плюс прибыль на всех последующих шагах была максимальной.
Беллманом было сформулировано основное требование, при котором принцип верен: процесс управления должен быть без обратной связи. Значит, управление на данном шаге не должно влиять на предшествующие шаги. Иногда системы, которые удовлетворяют указанному требованию, называют физически возможными, и они составляют подавляющее большинство систем, которые встречаются экономистам и инженерам на практике.
Казалось бы, принцип Беллмана только запутал ситуацию. Найти оптимальную политику, рассматривая процесс управления в целом, – сложная, практически невыполнимая задача. Надо разбивать управление на шаги. Принимая решение на отдельном этапе, надо думать обо всем управлении целиком. Получается замкнутый круг. Однако есть один этап, на котором можно не задумываться о том, что случится с системой дальше. Это последний шаг (n). На этом шаге можно выбрать такое условное управление, которое принесет максимальную выгоду (условным управление считается потому, что оно рассчитывается из предположения, что на предыдущем шаге возможны различные решения). Далее можно перейти к шагу n – 1 и, зная, как нужно поступить на последнем шаге, оптимизировать его, и т.д., пока не дойдем до первого шага. Таким образом, у нас получится оптимальная политика и будет рассчитан оптимальный выигрыш W.
Затем нужно пройти пошаговый процесс управления в обратном (естественном) порядке. По договоренности, нам известно первоначальное состояние системы S0. Зная его, можно рассчитать безусловное оптимальное управление х1 на первом шаге. Далее, на основе условного оптимального управления, на втором шаге можно найти оптимальное управление х2 и т.д. до последнего шага n.
|
|
|
Получается, что при решении задачи ДП приходится делать двойную прогонку процесса управления. Первый раз от последнего шага к первому, второй раз – от первого шага к последнему. Естественно, что первая прогонка значительно сложнее.
Рассмотрим иллюстрирующий пример.
П р и м е р 1.1 (прокладка оптимального пути между двумя пунктами). Необходимо соорудить путь, соединяющий два пункта А и В, который имеет минимальную стоимость, если пункт В находится на северо-востоке от пункта А.
Для простоты положим, что любой путь из А в В представляет собой ломаную, состоящую из отрезков, направленных строго на север или строго на восток. Затраты на сооружение каждого из отрезков заданы на рисунке 1.2.
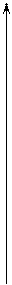 у (север) у (север)
        (0; 5) 10 13 10 8 9 11 10 В(7; 5)
11 12 10 11 11 12 13 14 (0; 5) 10 13 10 8 9 11 10 В(7; 5)
11 12 10 11 11 12 13 14
 8 9 14 10 9 12 14
10 13 11 15 10 10 9 8 8 9 14 10 9 12 14
10 13 11 15 10 10 9 8
 10 12 13 10 8 10
11 15 12 14 15 10 9 11 10 12 13 10 8 10
11 15 12 14 15 10 9 11
 8 10 11 13 16 12
12 14 11 10 12 11 10 12 8 10 11 13 16 12
12 14 11 10 12 11 10 12
 12 10 15 13 15 10
10 11 12 12 11 10 12 15 12 10 15 13 15 10
10 11 12 12 11 10 12 15
 14 14 13 12 10 14 13
А (0; 0) (7; 0) х (восток) 14 14 13 12 10 14 13
А (0; 0) (7; 0) х (восток)
|
Рис. 1.2.
Решение. Начнем решение с последнего этапа (рис. 1.3). На последнем
   (6; 5) 10 В(7; 5)
13 14 (6; 5) 10 В(7; 5)
13 14
 14
(6; 4) (7; 4)
Рис. 1.3. 14
(6; 4) (7; 4)
Рис. 1.3.
| этапе в точку В можно попасть из точки с координатами (6; 5) или из точки с координатами (7; 4). Цена участка (6; 5) ® В меньше. Следовательно, выбирается участок, ведущий на восток. |
На предпоследнем этапе в точку (6; 5) можно попасть из точки (5; 5) и (6; 4). Минимальные затраты будут на участке (5; 5) ® (6; 5). И так далее до точки А (0; 0). Оптимальный маршрут В(7; 5) ® (6; 5) ® (5; 5) ® (4; 5) ®
®(3; 5) ® (2; 5) ® (2; 4) ® (1; 4) ® (0; 4) ® (0; 3) ® (0; 2) ® (0; 1) ® А(0; 0) изображен на рисунке 1.4. Его стоимость равна:
10 + 11 + 9 + 8 + 10 + 10 + 9 + 8 + 10 + 11 + 12 + 10 = 118 (у.е.).
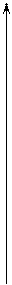 у (север) у (север)
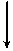              (0; 5) В(7; 5) (0; 5) В(7; 5)

А (0; 0) (7; 0) х (восток) |
Рис. 1.4.
Из всех маршрутов выбранный будет наиболее дешевым. 5
Решение примера 1.1 получено достаточно простым способом (последовательным перебором) благодаря тому, что не так много было вариантов развития событий. Во многих задачах ДП дело обстоит гораздо хуже. Вообще говоря, динамическое программирование достаточно «демократично» в смысле постановки задачи. Ему не страшны, в отличие от ЛП, требования целочисленности решений, линейности целевой функции и ограничений. Однако для ДП не существует такого универсального метода решения, каким является симплексный метод в ЛП. К тому же сложность решения задачи ДП существенно возрастает при возрастании размерности.
|
|
|
П.2. Уравнение Беллмана
Вернемся к задаче ДП, графическое представление которой дано на рис. 1.1.
Пусть прибыль на каждом отдельном этапе k есть функция, зависящая от состояния системы на предыдущем шаге k – 1 и решения xk, принятого на данном этапе wk(S) = f(Sk – 1, xk).
Начнем решение задачи с последнего этапа. В этом случае условный максимум целевой функции будет определяться по формуле
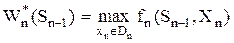 .
.
Здесь Dn – множество допустимых решений на последнем этапе. Пусть найден условный максимум целевой функции ( ) и условное оптимальное управление (
) и условное оптимальное управление ( ) на последнем шаге. Значение целевой функции будет равно
) на последнем шаге. Значение целевой функции будет равно
Wn – 1(Sn – 2) = fn – 1(Sn – 2, Xn – 1) +  . (*)
. (*)
Заметим, что в выражение (*) входит состояние системы Sn – 1. Поэтому, чтобы продолжить решение, необходимо определить, как изменяется система S под влиянием управления Хk на k-ом шаге
Sk = jk(Sk – 1, Хk).
Таким образом, условный максимум целевой функции на n – 1 шаге определяется по формуле:
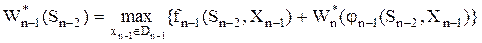 .
.
Пусть найден условный максимум  и условное оптимальное управление
и условное оптимальное управление  . Перейдем к шагу n – 2 и т.д.
. Перейдем к шагу n – 2 и т.д.
На k-ом шаге (n – k + 1 шаг с конца) получим:
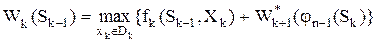 . (1.1)
. (1.1)
Уравнение (1.1) называется уравнением Беллмана.
Решая последовательно уравнение Беллмана на каждом шаге, получим условные максимумы целевой функции  ®
® 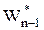 ® …
® …  и условное оптимальное управление
и условное оптимальное управление  ®
®  ® …
® … 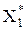 .
.
Далее остается по известному состоянию S0 определить состояние S1 и найти максимум W1 и оптимальное управление Х1 и т.д. по цепочке.
Таким образом, алгоритм решения задачи ДП с использованием уравнения Беллмана следующий.
1. Определяются параметры, которые характеризуют состояние системы S.
2. Разбивается процесс управления на шаги.
3. Определяется набор решений Xk (k = 1, …, n) и ограничения, которые на них накладываются.
4. Определяется функция прибыли
wk = fk(Sk – 1, Хk).
5. Определяется функция, показывающая, как меняется состояние системы под влиянием решения Хk.
Sk = j (Sk – 1, Хk).
6. Записывается уравнение Беллмана
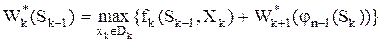 .
.
7. Проводится условная оптимизация, начиная с последнего шага n до первого.
8. Проводится безусловная оптимизация, начиная с первого шага до последнего.
Продемонстрируем изложенную схему на примере решения задачи о финансировании предприятий.
П р и м е р 1.2. В начале года банк имеет возможность вложить в два предприятия средства в размере a денежных единиц. От вложения на квартал в первое предприятие х денежных единиц банк получает доход в размере bx денежных единиц и остаток средств в размере рх единиц. Для второго предприятия эти показатели составляют соответственно сх и lx денежных единиц. В каждом последующем квартале могут использоваться только остатки денежных средств.
|
|
|
Определить программу квартального выделения средств каждому предприятию, обеспечивающую банку наибольший годовой (4 квартала) доход.
а = 5000 у.е.; b = 3; c = 2,4; d = 0,5; l = 0,7.
Решение.
1) В данном случае состояние системы характеризуется остатком средств, которые могут быть использованы на дальнейшее финансирование предприятий.
2) Число шагов, следуя условию задачи, необходимо выбрать по числу кварталов n = 4.
3) Пусть двум предприятиям выделяют на k-том этапе ak средств. Из них первому предприятию xk, второму yk. Ограничения имеют вид:
xk + yk = ak, xk ³ 0, уk ³ 0 (k = 1, 2, 3, 4).
Таким образом, решение будет заключаться в нахождении объема финансирования одного из двух предприятий.
4) Определим функцию прибыли:
wk = 3 xk + 2,4 yk = 3 xk + 2,4 (ak – xk) = 2,4 ak + 0,6 xk.
Здесь мы воспользовались тем, что yk = ak – xk.
5) Найдем функцию, определяющую изменение состояния системы в зависимости от решения на k-ом этапе. Для этого необходимо рассчитать остаток средств на k + 1 этапе.
Sk + 1 = j (Sk, (xk, yk)) = 0,5 xk + 0,7 yk = 0,5 xk + 0,7 (ak – xk) = 0,7 ak – 0,2 xk.
6) Уравнение Беллмана будет иметь вид:
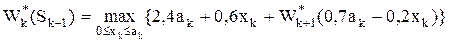 .
.
7) Проведем условную оптимизацию.
Начнем процесс условной оптимизации с последнего этапа, т.е. k = 4, а остаток равен 0, т.е. Wk + 1 = 0.
 .
.
Условное оптимальное решение на 4-м этапе будет такое: профинансировать первое предприятие в размере а4 у.е., второе предприятие не финансировать (х4 = а4, у4 = а4 – х4 = 0).
k = 3.
 .
.
На третьем этапе никакие решения не повлияют на условный максимум 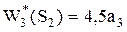 , поэтому средства в размере а3 у.е. можно распределить произвольно между предприятиями.
, поэтому средства в размере а3 у.е. можно распределить произвольно между предприятиями.
k = 2.

Условное оптимальное решение на 2-м этапе: выделить все средства в размере а2 у.е. второму предприятию, первое предприятие не финансировать (х2 = 0, у2 = а2).
k = 1.
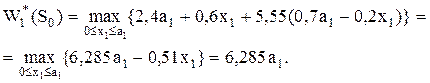
На первом этапе условный максимум достигается, если профинансировать второе предприятие, а первому предприятию средств не выделять (х1 = 0, у1 = а1). Условная оптимизация проведена.
8) Проведем безусловную оптимизацию. На первом шаге выделяется
а1 = 5000 у.е. Значит, S1 = 5000 у.е., 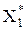 (х1 = 0, у1 = 5000).
(х1 = 0, у1 = 5000).  = 31425 у.е. – прибыль за все четыре шага.
= 31425 у.е. – прибыль за все четыре шага.
На втором шаге S2 = а2 = 0,7 a1 – 0,2 x1 = 0,7 × 5000 – 0,2 × 0 = 3500 у.е.,  (х2 = 0, у2 = 3500),
(х2 = 0, у2 = 3500), 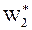 = 19425 у.е. – суммарная максимальная прибыль на 2, 3, 4 шагах.
= 19425 у.е. – суммарная максимальная прибыль на 2, 3, 4 шагах.
На третьем шаге S3 = а3 = 0,7 a2 – 0,2 x2 = 0,7 × 3500 – 0,2 × 0 = 2450 у.е., 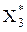 (0 £ х2 £ 2450, у3 = 2450 – х3),
(0 £ х2 £ 2450, у3 = 2450 – х3), 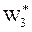 = 11025 у.е. – суммарная максимальная прибыль на 3 и 4 шагах.
= 11025 у.е. – суммарная максимальная прибыль на 3 и 4 шагах.
k = 4. S4 = а4 = 0,7 a3– 0,2 x3 = 1715 –0,2 х3,  (х4 = 1715 – 0,2 х3, у3 = 0),
(х4 = 1715 – 0,2 х3, у3 = 0), 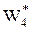 = 3 (1715 – 0,2 х3). 5
= 3 (1715 – 0,2 х3). 5
Заметим, что в данной задаче ДП существует бесконечно много оптимальных стратегий, приводящих к одной и той же оптимальной прибыли. Такая ситуация является достаточно типичной для ДП.
|
|
|



