 |
П.2. Классические методы оптимизации
|
|
|
|
Сразу отметим, что для решения задач НП не существует такого универсального метода, как симплексный метод для задач ЛП.
В данном случае рассмотрим классический метод поиска условного экстремума – метод множителей Лагранжа.
Для этого напомним несколько необходимых определений и утверждений.
Пусть функция Z = f(x1, x2, …, xn) дифференцируема в точке Х0( ,
,  , …,
, …,  ),
),  (l 1, l 2, …, l n) – единичный вектор (|
(l 1, l 2, …, l n) – единичный вектор (|  | = 1).
| = 1).
Производной функции Z по направлению  в точке Х0 называется
в точке Х0 называется
 .
.
Можно показать, что
 ,
,
где все частные производные вычисляются в точке Х0.
Градиентом функции Z = f(x1, x2, …, xn) (grad Z) в точке Х0 называется вектор с координатами  .
.
Направление grad Z – это направление, производная по которому от функции достигает наибольшего значения.
Рассмотрим матрицу из вторых частных производных функции
Z = f(x1, x2, …, xn)
 . (3.3)
. (3.3)
Такая матрица получила название матрицы Гессе функции Z = f(x1, x2, …, xn). В силу равенства смешанных производных, матрица Гессе – симметричная матрица.
В частности, для функции двух переменных матрица Гессе имеет вид:
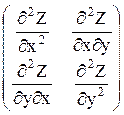 .
.
Справедливы следующие утверждения.
Теорема 3.1 (необходимое условие существования экстремума). Если функция Z = f(x1, x2, …, xn) дифференцируема в точке Х0( ,
,  , …,
, …,  ) и имеет в этой точке локальный экстремум, то в этой точке grad Z = 0.
) и имеет в этой точке локальный экстремум, то в этой точке grad Z = 0.
Другими словами, в точке локального экстремума все частные производные первого порядка равны нулю.
Теорема 3.2 (достаточное условие существования экстремума). Если функция дважды дифференцируема в окрестности точки Х0, первые частные производные в этой точке равны нулю, матрица Гессе в этой точке положительно определена[1], то функция в этой точке имеет строгий локальный минимум (если матрица Гессе отрицательно определена, то строгий локальный максимум).
|
|
|
Все приведенные утверждения дают метод для поиска локальных экстремумов. Однако задача ДП сводится к поиску условного экстремума функции.
Рассмотрим метод множителей Лагранжа. Основная его идея – свести с помощью вспомогательной функции задачу поиска условного экстремума к задаче поиска локального экстремума.
Рассмотрим задачу ДП.
Z = f(x1, x2, …, xn) ® max (min),

Составим вспомогательную функцию
F(x1, x2, …, xn, l1,…, lm) = f(x1, x2, …, xn) +  .
.
Здесь l1,…, lm – постоянные множители (множители Лагранжа). Множителям Лагранжа можно дать экономическую интерпретацию. Если
Z = f(x1, x2, …, xn) – доход, соответствующий плану Х(x1, x2, …, xn), gk(X) = bk (k = 1,…, m) – издержки k-го ресурса, то lk – маргинальная оценка[2], которая характеризует изменение экстремального значения функции в зависимости от k-го ресурса.
Функция Лагранжа достигает экстремума для тех же значений переменных x1, x2, …, xn, что и целевая функция Z. Остается исследовать функцию Лагранжа на локальный экстремум.
Общую схему метода множителей Лагранжа можно представить следующим образом.
1. Составляется функция Лагранжа.
2. Находятся частные производные функции Лагранжа по переменным x1, …, xn, l1,…, lm.
3. Находятся точки, в которых целевая функция может иметь экстремум, т.е. точки, в которых все частные производные равны нулю.
4. Проверяются на экстремум точки, определенные на третьем этапе по матрице Гессе.
Рассмотрим реализацию метода множителей Лагранжа на примере.
П р и м е р 3.1. Найти минимум целевой функции
Z = 4 х1 + х12 + х12
при ограничении
х1 + х2 = 200.
Решение.
1) Составим функцию Лагранжа
F(x1, x2, l1) = 4 х1 + х12 + х12 + l1(200 – х1 – х2).
2) Найдем частные производные

3) Составим систему уравнений для определения точек, подозрительных на экстремум
 (*)
(*)
Решая систему (*), получим

4) Матрица Гессе функции Лагранжа по переменным х1 и х2 имеет вид:
 .
.
|
|
|
Данная матрица является положительно определенной, т.е. Х(99; 101) - оптимальный план задачи.
Zmin = Z(99; 101) = 20398. 5
П.3. Выпуклые функции
Определение 3.4. Функция F(X) (Х = Х(x1, x2, …, xn)), определенная на выпуклом множестве D, называется вогнутой, если на множестве D для любых Х1 ÎD и Х2 ÎD выполняется условие
F(a X1 + (1 – a) X2) ³ a F(X1) + (1 – a) F(X2).
Выяснить, является ли функция выпуклой или вогнутой, можно, используя матрицу Гессе.
Справедливы следующие утверждения.
Теорема 3.1. Пусть функция F(Х) определена на выпуклом множестве D и имеет на этом множестве непрерывные частные производные второго порядка. Функция F(Х) выпукла на множестве D тогда и только тогда, когда ее матрица Гессе положительно определена.
Теорема 3.2. Пусть функция F(Х), определенная на некотором множестве D, имеет на этом множестве непрерывные производные второго порядка. Тогда F(Х) вогнута на множестве D в том и только в том случае, если знак главного минора [3] матрицы Гесса k-го порядка совпадает со знаком
(–1)k во всех точках множества D.
П р и м е р 3.2. Показать, что функция
Z = 4 х1 + х12 + х12
является выпуклой на всей области определения.
Решение. Матрица Гессе имеет вид:
 .
.
Данная матрица положительно определена, следовательно, функция
Z(x1, x2) выпукла на всей области определения. 5
П.4. Градиентный метод
Из всех задач НП обычно выделяют задачи выпуклого программирования (ВП). Задача нелинейного программирования (3.1), (3.2) называется выпуклой, если все функции gk(x1, x2, …, xn) являются выпуклыми на множестве D, а целевая функция Z(x1, x2, …, xn) выпукла или вогнута на множестве D.
Задачи выпуклого программирования заслуживают особого внимания, т.к. в силу свойств выпуклых функций локальный экстремум является глобальным. Значит, если область определения не пуста и ограничена, то задача ВП всегда имеет единственное решение.
Указанное свойство позволило широко применять к решению задач ВП численные методы. Рассмотрим один из таких методов, который получил название градиентный.
Суть градиентного метода заключается в том, что в окрестности рассматриваемой точки заданная целевая функция заменяется ее линейным приближением, получаемым из разложения функции в ряд Тейлора.
В процессе решения строится последовательность Х0, Х1, …, Хk … решений системы ограничений данной задачи ВП, причем решение Х0 выбирается, вообще говоря, произвольно. Последующие точки получаются из предыдущей по формуле
|
|
|
Хk+1 = Хk + ak  , (3.4)
, (3.4)
где ak – число,  = (l 1, l 2, …, l n) – направление некоторого вектора.
= (l 1, l 2, …, l n) – направление некоторого вектора.
В градиентном методе  ищется в зависимости от функции Z(X), поскольку направление grad Z является направлением ее скорейшего роста. Так для отыскания максимума целевой функции
ищется в зависимости от функции Z(X), поскольку направление grad Z является направлением ее скорейшего роста. Так для отыскания максимума целевой функции
 = grad Z(Xk), (3.5)
= grad Z(Xk), (3.5)
для минимума
 = – grad Z(Xk), (3.5¢)
= – grad Z(Xk), (3.5¢)
Для выбора шага ak существуют различные методы. Одним из самых распространенных является метод скорейшего спуска. В этом методе ak выбирается так, чтобы приращение функции DZ при перемещении из точки Хk в точку Хk+1 было наибольшим при отыскании максимального значения или наименьшим при отыскании минимума.
Таким образом, в методе скорейшего спуска для поиска шага ak необходимо исследовать на экстремум функцию
DZ = Z(Хk+1) – Z(Хk).
Заметим, что, поскольку точка Хk считается известной, то Z(Хk) и
grad Z(Хk) – постоянные величины. Напомним, что
grad Z(Хk) =  .
.
Получим необходимое условие экстремума функции DZ
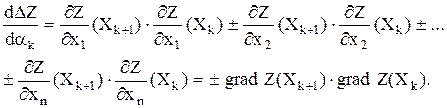
Верхний знак в выражении соответствует случаю Zmax, нижний – Zmin.
Таким образом, необходимое условие экстремума функции DZ имеет вид
grad Z(Хk+1) grad Z(Хk) = 0. (3.6)
Уравнение (3.6) является требованием перпендикулярности векторов grad Z(Хk+1) и grad Z(Хk), т.к. в левой части уравнения стоит скалярное произведение.
Пользоваться уравнением (3.6) для определения шага ak можно в том случае, когда оптимальное значение целевой функции находится внутри области допустимых значений. В этом случае точка Хk+1, найденная по формуле (3.4), остается в области определения функции D.
Если оптимальное значение достигается на границе области (например, в задаче ЛП) задача несколько осложняется. В этом случае на некотором шаге k может получиться так, что найденная по формуле (3.4) точка Хk не находится в области определения D. Тогда вместо точки Хk берется точка Хk¢, которая лежит на пересечении направления спуска и границы области решений (см. рис. 3.2).
|
|
|
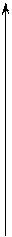 x2 x2
 Xk
Xk¢ Xk
Xk¢
l
D
x1 |
Рис. 3.2.
Надо отметить, что метод скорейшего спуска в общем случае является бесконечным, т.е. с каждым шагом оптимальное решение приближается, но достичь его удается только с определенной точностью. Однако в ряде задач можно найти оптимальное значение целевой функции за конечное число итераций.
П р и м е р 3.3. Используя метод скорейшего спуска, найти максимум целевой функции
Z = 3 – (x1 – 4)2 – (x2 – 5)2
при ограничениях

Решение. Проверим, является ли данная задача задачей ВП. Для этого составим матрицу Гессе.
 ,
,
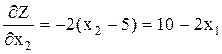 ,
,
 ,
,
 ,
,
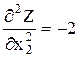 ,
,
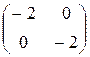 .
.
Главный определитель первого порядка равен –2 < 0. Главный определитель второго порядка равен 4 >0. Значит, целевая функция является вогнутой на всей области допустимых значений. Следовательно, ее локальный максимум совпадает с глобальным.
В качестве исходной точки возьмем точку Х0(1; 2) (Х0 Î D). Выражение градиента функции Z имеет вид:
 .
.
Найдем координаты точки Х1(х1¢, х2¢)
 ,
,
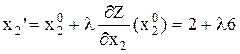 .
.
Определим значения градиента функции в точках Х0 и Х1.
 ,
,
 .
.
Найдем скалярное произведение найденных значений градиента и приравняем его к нулю.
6(6 – 12 l) + 6(6 – 12 l) = 0,
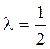 .
.
Следовательно,
 ,
,
 .
.
В точке Х1 значение градиента равно нулю
 .
.
Поскольку значение градиента в точке Х1 равно нулю, то точка Х1 – точка максимума
Zmax = Z(4; 5) = 3, (4; 3) Î D. 5
В данной задаче точное решение получилось после первой итерации, что, к сожалению, является редким исключением. Традиционно считается, что все задачи НП относятся к наиболее трудоемким задачам исследования операций. Для их решения используются специальные пакеты программ (Mathcad и др.).
Проверочные вопросы
1. Приведите общую постановку задачи динамического программирования.
2. Сформулируйте принцип Беллмана.
3. Уравнение Беллмана.
4. Условная пошаговая оптимизация.
5. Безусловная пошаговая оптимизация.
6. Сформулируйте общий алгоритм решения задачи динамического программирования.
7. Назовите область применения сетевого планирования.
8. Назовите основные компоненты сетевого графика.
9. Перечислите основные требования к построению сетевого графика.
10. Какие виды работ используются в сетевом планировании?
11. Сформулируйте понятие критического пути.
12. Ранний срок совершения события.
13. Поздний срок совершения события.
14. Резерв времени.
15. Нахождение критического пути с помощью временных параметров событий.
16. Сетевое планирование в условиях неопределенности.
17. Две основные задачи сетевого планирования в условиях неопределенности.
18. Задача нелинейного программирования в канонической форме.
19. Понятия локального и глобального экстремумов.
|
|
|
20. Необходимое и достаточное условие существования экстремума.
21. Метод множителей Лагранжа.
22. Матрица Гессе и ее применение.
23. Выпуклые функции и их свойства.
24. Градиентный метод решения задач нелинейного программирования.
[1] Матрица называется положительно определенной, если ее миноры положительны.
[2] marginalis (от лат.) – находящийся на краю.
[3] Главный минор матрицы – это минор, в котором по главной диагонали номера строк совпадают с номерами столбцов.
|
|
|




