 |
П.3. Критический путь, параметры событий
|
|
|
|
Одним из основных понятий сетевого графика является понятие критического пути.
Критический путь – это наиболее продолжительный путь в сетевом графике, начало которого совпадает с начальным событием, а конец с конечным событием.
Все работы и события, лежащие на критическом пути, называются критическими.
Продолжительность критического пути определяет общую продолжительность всего комплекса работ и является минимальным временем, необходимым для выполнения проекта. Как правило, если необходимо сократить сроки выполнения проекта, то в первую очередь нужно обратить внимание на критические события и критические работы.
Как же найти критический путь? Первое, что приходит в голову, это перебрать все возможные пути, ведущие от начального события к конечному, и выбрать из них самый продолжительный. Этот прием, конечно, можно использовать, если число событий и работ небольшое. Однако в таких случаях можно вообще обойтись без сетевого планирования. На практике и число событий, и число работ достаточно велико, поэтому простой перебор оказывается достаточно громоздкой процедурой.
Одним из эффективных методов поиска критического пути является использование временных параметров событий.
Ранний срок совершения k-го события tp(k) определяется из максимального по продолжительности пути, идущего от начального события к
k-му событию.
Пусть событию k предшествуют несколько событий, которые мы обозначим через i, тогда
 . (*)
. (*)
Для начального события tp(1) = 0.
Смысл формулы (*) состоит в том, что событие k может произойти не раньше, чем закончатся все предыдущие работы. Согласно формуле (*), необходимо к ранним срокам всех предшествующих событию k событий i прибавить продолжительность работ (i; k). Из полученных значений выбирается максимальное. Ранний срок совершения последнего события будет равен tкр.
|
|
|
П р и м е р 2.1 (продолжение). Найти ранние сроки совершения событий и длину критического пути, используя рис. 2.3.
Решение. Ранний срок совершения 1-го события равен 0. 2-му событию предшествует только событие 1.
tp(2) = tp(1) + t(1; 2) = 0 + 8 = 8.
3-му событию предшествует второе, значит
tp(3) = tp(2) + t(2; 3) = 8 + 4 = 12.
4-му событию предшествуют 2 и 1,
tp(4) = max (tp(1) + t(1; 4); tp(2) + t(2; 4)) = max (0+13; 8+6) = max (13; 14) = 14.
5-му событию предшествуют 4 и 2,
tp(5) = max (tp(2) + t(2; 5); tp(4) + t(4; 5)) = max (8+9; 14+10) = 24.
6-му событию предшествуют 4 и 1,
tp(6) = max (tp(1) + t(1; 6); tp(4) + t(4; 6)) = max (0+9; 14+6) = 20 и т.д.
Результаты всех вычислений приведены в таблице 2.2.
Таблица 2.2.
| Событие | tp(k) | tп(k) | Резерв времени R(k) | Краткий путь |
 1 1
| ||||
 2 2
| ||||
 4 4
| ||||
 5 5
| ||||
 7 7
| ||||
 10 10
| ||||
 11 11
| ||||
| tкр = 65 |
tp(12) = 65 – это минимальный срок для проведения всего комплекса работ, т.е. tкр = tp(12) = 65 (ч.).
Таким образом, ранний срок совершения последнего события совпадает с продолжительностью критического пути. 5
Заметим, что при решении поставленной задачи на каждом этапе рассматривается не весь сетевой график, а только одно определенное событие и предшествующие ему события и работы.
В примере 2.1 продолжительность критического пути найдена, однако остается невыясненной его топология, т.е. события и работы, лежащие на критическом пути. Для того, чтобы их определить, найдем поздний срок совершения события k (tп(k)).
Поздний срок совершения k-го события определяется как максимальное время совершения события k, при котором не изменится tкр. При расчете позднего срока совершения события k мы должны учитывать последствия для всего дальнейшего комплекса работ. Поэтому, следуя основным принципам ДП, расчет должен начинаться от последнего события и идти к начальному. Для конечного события будем считать, что его ранний и поздний срок совершения совпадают.
|
|
|
Если k-ому событию предшествуют несколько событий, которые обозначим через m, то
 .
.
П р и м е р 2.1 (продолжение). Определить поздние сроки совершения событий.
Решение. Для последнего события справедливы соотношения
tп(12) = tp(12) = tкр = 65 (ч.).
11-му событию следует событие 12
tп(11) = tп(12) – t(11; 12) = 65 – 13 = 52 (ч.).
10-му событию следуют события 11 и 12
tп(10) = min (tп(12) – t(10; 12); tп(11) – t(10; 11)) = min(65 – 17; 52 – 7) = 45.
9-му событию следует событие 10
tп(9) = tп(10) – t(9; 10) = 45 – 4 = 41.
8-му событию следуют события 11 и 12
tп(8) = min (tп(11) – t(8; 11); tп(12) – t(8; 12)) = min(52 – 5; 65 – 5) = 47.
7-му событию следуют события 9, 10 и 11
tп(7) = min (tп(9) – t(7; 9); tп(10) – t(7; 10); tп(11) – t(7; 11)) =
= min(41 – 8; 45 – 13; 52 – 5) = 32.
и т.д.
Результаты всех вычислений приведены в таблице 2.2. 5
Разность между поздним и ранним сроком совершения события называется резервом времени (R(k)).
R(k) = tп(k) – tр(k). (2.1)
События, расположенные на критическом пути, не имеют резервов времени.
Таким образом, с помощью раннего срока наступления событий можно определить продолжительность критического пути, с помощью позднего срока окончания событий можно определить топологию критического пути.
П р и м е р 2.1 (продолжение). Найти резервы времени и события, находящиеся на критическом пути.
Решение. Рассчитываем по формуле (2.1) резервы времени. Результаты вычислений представлены в таблице 2.2. События 1, 2, 4, 5, 7, 10, 11, 12 резервов времени не имеют. Следовательно, критический путь имеет вид:
1 ® 2 ® 4 ® 5 ® 7 ® 10 ®11 ® 12. 5
П.4. Сетевое планирование в условиях неопределенности
В предыдущих пунктах предполагалось, что параметры работ точно известны. На практике гораздо чаще встречаются ситуации, когда параметры работ являются случайными величинами и характеризуются определенными моментами (например, математическим ожиданием и средним квадратическим отклонением).
Обозначим математическое ожидание продолжительности работы (k, m) через M(t(k, m)), среднее квадратическое отклонение через s(k, m).
|
|
|
Наиболее часто для характеристики продолжительности отдельной работы используется b-распределение.
Пусть на критическом пути достаточно много работ, причем выполняются условия законов больших чисел. Тогда согласно центральной предельной теореме Ляпунова, можно считать, что общая продолжительность работы на критическом пути имеет нормальный закон распределения с параметрами:
 ,
,
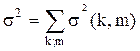 .
.
Данные предположения могут быть использованы для решения ряда важных задач сетевого планирования и управления, а именно:
1) оценить вероятность того, что проект будет выполнен к определенному времени;
2) по заданной надежности определить срок выполнения проекта.
П р и м е р 2.1 (продолжение). Пусть указанные в таблице 2.1 продолжительности работ являются математическими ожиданиями соответствующих работ. Причем для работ, лежащих на критическом пути, выполняются условия:
s2(1; 2) = s2(2; 4) = s2(4; 5) = s2(5; 7) = s2(7; 10) = 1, s2(10; 11) = s2(11; 12) = 2.
Определить:
1) вероятность того, что проект будет выполнен в срок Т = 68 ч.;
2) определить максимально возможный срок Т выполнения проекта с надежностью g = 0,95.
Решение.
1) Определим вероятность того, что проект будет выполнен в срок
Т = 68 по формуле (см. [19]):
 ,
,
где Ф(t) – функция Лапласа;
а = 65;
 .
.
Получим
 .
.
2) Максимально возможный срок выполнения проекта с надежностью
g = 0,95 найдем по формуле (см. [9]):
Tmax = a + t0,95 × s,
где t0,95 = 1,96 – квантиль уровня 0,95 стандартного нормального распределения.
Получим
Tmax = 65 + 1,96 × 3 = 70,88» 71. 5
|
|
|


