 |
Идентификация эконометрических уравнений.
|
|
|
|
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – единственность соответствия между структурной и приведенной формами модели.
Параметры структурной формы модели по оценкам приведенных коэффициентов можно определить не всегда. Для этого необходимо, чтобы модель была идентифицируемой.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
Выделяют:
1) Точно идентифицируемая модель – все ее уравнения точно идентифицированы. То есть все структурные коэффициенты определяются однозначно (единственным способом) по коэффициентам приведенной формы модели. И число параметров структурной модели равно числу параметров приведенной формы.
2) Неидентифицируемая модель – число приведенных коэффициентов меньше числа структурных коэффициентов. Оценки всех структурных параметров невозможно найти по коэффициентам приведенной модели.
3) Сверхидентифицируемая модель – число приведенных коэффициентов больше числа структурных коэффициентов (на основе приведенной формы можно получить 2 и более значений одного структурного коэффициента). Практически решаема, но требует применения специальных методов.
На идентификацию проверяются все уравнения модели. Модель считается идентифицируемой, если все уравнения идентифицируемы; сверх – если хоть одно сверхидентифицируемо, а остальные точно идентифицируемы. Если среди всех уравнений модели есть хотя бы одно неидентифицированное, то вся модель считается неидентифицированной.
Правила идентификации
Введем следующие обозначения:
М- число экзогенных (предопределенных) переменных в модели;
|
|
|
т- число экзогенных (предопределенных) переменных в данном уравнении;
К - число эндогенных переменных в модели;
k - число эндогенных переменных в данном уравнении.
А) Необходимое (но недостаточное) условие идентификации.
Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1», т.е.: 
;
Если 
, уравнение точно идентифицировано.
Если , уравнение сверхидентифицировано.
Либо D+1=H (H – число эндогенных переменных в уравнении; D – число отсутствующих экзогенных переменных).
Эти правила следует применять к структурной форме модели.
Достаточное условие идентификации. Введем обозначения: А - матрица коэффициентов при переменных не входящих в данное уравнение.
Достаточное условие идентификации заключается в том, что
- определитель матрицы А должен быть не равен нулю,
- ранг матрицы А должен быть не меньше, чем число эндогенных переменных в системе без одного 
.
Ранг матрицы - размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю. Пример:
a b
c d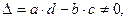 
тогда ранг R=2.
Сформулируем необходимое и достаточное условия идентификации:
1) Если и ранг матрицы А 
равен , то уравнение сверхидентифицировано.
2) Если и ранг матрицы А , то уравнение точно идентифицировано.
3) Если 
и ранг матрицы А < то уравнение неидентифицированно.
4) Если 
, то уравнение неидентифицированно. В этом случае ранг матрицы А будет меньше .
Оценка точно идентифицированного уравнения осуществляется с помощью косвенного метода наименьших квадратов (КМНК).
Алгоритм КМНК включает 3 шага:
1) составление приведенной формы модели и выражение каждого коэффициента приведенной формы через структурные параметры;
2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;
|
|
|
3) определение оценок параметров структурной формы по оценкам приведенных коэффициентов, используя соотношения, найденные на шаге 1.
Оценка сверхидентифицированного уравнения осуществляется при помощи двухшагового метода наименьших квадратов.
Алгоритм двухшагового МНК включает следующие шаги:
1) составление приведенной формы модели;
2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;
3) определение расчетных значений эндогенных переменных, которые фигурируют в качестве факторов в структурной форме модели;
4) определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на шаге 1.
|
|
|
