 |
Интерпретация параметров моделей авторегрессии.
|
|
|
|
Модели содержащие в качестве факторов лаговые значения зависимой переменной называются моделями авторегрессии. Например, 
Как и в модели с распределенным лагом,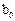 
и в этой модели характеризует краткосрочные изменения 
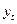под воздействием изменения 
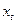на 1 ед. Однако промежуточные и долгосрочные мультипликаторы иные. К моменту времени 
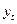результат изменился под воздействием изменения фактора в момент времени t на 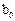ед., а 
под воздействием свого изменения в непосредственно предшествующий момент времени – на 
ед. таким образом, общее абсолютное изменение результата в момент составит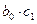 
ед. Аналогично в момент времени 
абсолютное изменение результат составит 
ед. и т.д.
Следовательно, долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов:
где 
Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличие бесконечного лага в воздействии текущего знач. зависимой переменной на ее будущее значения.
Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки МНК, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Применительно к моделям авторегрессии необходимо удалить из правой части модели переменную 
. Искомая новая переменная, которая будет введена в модель вместо должна иметь два свойства. Во-первых, она должна тесно коррелировать , во-вторых, она не должна коррелировать с остатками 
. Еще один метод, который можно применять для оценки параметров моделей авторегрессии типа — это метод максимального правдоподобия.
|
|
|
Применение метода Алмон для расчета параметров модели с распределенным лагом.
Текущие и лаговые значения факторной переменной оказывают различное по силе воздействие на результативную переменную модели. Качественно сила связи между результатом и значениями факторной переменной, относящимися к различным моментам времени, измеряется с помощью коэффициентов регрессии при факторных переменных. Если построить график зависимости этих коэффициентов от величины лага, можно получиться графическое изображение структуры лага, или распределения во времени воздействия факторной переменной на результат. Структура лага может быть различной.
Также графический анализ структуры лага можно с помощью относительных коэффициентов регрессии 
Основная трудность в выявлении структуры лага состоит в том, как получить значения параметров 
(или 
). Обычный МНК редко бывает полезным в этих целях.
Метод Алмона
Рассмотрим общую модель с распределенным лагом, имеющую конечную максимальную величину лага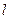 
, которая описывается соотношением: 
В методе Алмона предполагается, что в исследуемой модели имеет место полиномиальная структура лага, т.к. зависимость коэффициентов регрессии от величины лага описывается полиномом k-й степени. Таким образом, лаги Алмон – лаги, структуру которых можно описать с помощью полиномов.
Формально модель зависимости коэффициентов от величины лага j в форме полинома можно записать в следующем виде: 
Тогда каждый из коэф-ов модели можно выразить след. обр.:
Тогда модель с распределенным лагом примет вид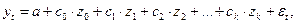 
где 
Процедура применения метода Алмон для расчета параметров модели с распределенным лагом проводится по следующей схеме:
|
|
|
1.Устанавливается макс. величина лага 
2.Определяется степень полинома k, описывающего структуру лага.
3. Рассчитывается значение переменных с z0 до zk.
4. Определяются параметры уравнения линейной регрессии 
5.Рассчитываются параметры b исходной модели с распределенным лагом с помощью ранее найденных соотношений.
Проблемы применения метода Алмон:
- величина лага 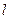должна быть известна заранее; при определении лучше исходить из максимально возможного лага;
- необходимо установить степень полинома (должна быть на 1 больше числа экстремумов в структуре лага);
- переменные z, определяемые как линейные комбинации исходных переменных х, коллелируют между собой, если существует высокая связь между исходными переменными х.
Преимущества метода Алмон:
- он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов;
- при относительно небольшом количестве переменных можно построить модели со степенью полинома 2 или 3, которые не приводят к потере значительного числа степеней свободы.
- можно построить модели с распределенным лагом любой длины.
|
|
|
