 |
Обтекание шара при малых числах Рейнольдса.
|
|
|
|
Первое теоретическое решение для обтекания шара ламинарным потоком и формула для силы, действующей при этом на шар, принадлежит Г. Стоксу.
Выражение для силы 
, действующей на шар имеет вид:
, (11.7)
где 
– коэффициент динамической вязкости жидкости, 
– скорость набегающего потока (на бесконечности), 
– радиус шара.
Эта же формула (11.7) применима, когда шар движется в неподвижной жидкости. Заметим, что одна треть всей силы возникает вследствие разностей давлений в передней и кормовой частях шара, а две трети – вследствие сил трения. Отметим также, что сила сопротивления пропорциональна первой степени скорости.
Придадим формуле Стокса такой же вид, какой имеет формула Ньютона:
,
т.е. представим силу как произведение коэффициента сопротивления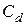 
на площадь 
поперечного сечения шара и на динамическое давление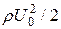 
, в результате получим:
;
Заменив его значением из (5.7) возможно найти коэффициент сопротивления
, (11.8)
где 
есть число Рейнольдса.
Сравнение формулы (11.8) с результатами измерений показывает, что она верна только в области чисел Рейнольдса 
.
Решение Стокса было улучшено К. Озееном путём частичного учёта инерционных членов в исходных уравнениях.
Для коэффициента сопротивления решение Озеена даёт зависимость:
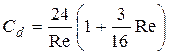, (11.9)
где как и раньше есть число Рейнольдса. Результаты измерений показывают, что формула (11.9) пригодна вплоть до числа 
.
Задача 11.2. Шарик из свинца равномерно опускается в глицерине, кинематический коэффициент вязкости которого 
= 12,8 см2/с. Определить наибольший диаметр шарика, при котором обтекание его ещё остаётся ламинарным. Считать, что переход к турбулентному характеру обтекания соответствует числу 
= 1,0 (
)
|
|
|
Определение вязкости жидкости с помощью формулы Стокса.
На небольшой шарик, падающий в жидкость, плотность которой меньше, чем плотность материала шарика, действуют три силы:
1. Сила тяжести
, (11.10)
где – радиус шарика, 
– плотность материала, из которого сделан шарик.
2. Выталкивающая сила (сила Архимеда).
, (11.11)
где 
– плотность жидкости. В формулах (5.10) и (5.11) объём шарика обозначен символом 
.
3. Сила сопротивления
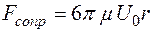, (11.12)
где – динамический коэффициент вязкости, – скорость падения шарика.
Сила тяжести направлена вниз, выталкивающая сила – вверх, а сила сопротивления всегда направлена в сторону противоположную движению.
Первые две силы по величине постоянные, а сила сопротивления пропорциональна скорости . Поэтому при ускоренном (из состояния покоя) движении выталкивающая сила и сила сопротивления в сумме уравновешивают силу тяжести, и шарик начинает двигаться равномерно.
При равномерном движении:
(11.13)
или
= 
+ 
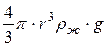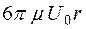(11.14)
В опытах обычно используют шарики малых размеров, чтобы выполнялось условие <1. Измерив в опытах скорость равномерного падения небольших шариков в жидкости возможно по формуле (11.14) определить вязкость жидкости .
Задача 11.3 Металлический шарик диаметром 
= 1,2мм начиная двигаться из состояния покоя за время 
опускается на дно сосуда, наполненного смазочным маслом. Высота столба масла в сосуде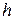 
= 0,8 м. Диаметр сосуда значительно больше диаметра шарика.
Определить коэффициент динамической вязкости масла. Плотность материала шарика 
= 7,8∙103 кг/м3, масла 
= 0,88∙103 кг/м3. Всего проделано пять измерений времени: 
= 22 с;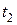 
= 24 с; 
= 23 с; 
= 22 с;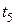 
= 23 с.
Решение
Так как масло обладает значительной вязкостью, то можно считать, что шарик сразу после опускания начинает двигаться равномерно. Так как ускорение равно нулю, то уравнение движения будет выражать собой равенство нулю результирующей силы, действующей на шар, т.е.
|
|
|
,
где 
– сила Архимеда, 
– сила сопротивления движению шарика.
Предположим, что сила сопротивления зависит от вязкости, т.е. . Силу сопротивления, в этом случае, возможно определить по формуле Стокса
,
где – радиус шара, – коэффициент динамической вязкости, 
– скорость движения шара.
Уравнение движения в этом случае примет вид
,
Откуда получается зависимость для коэффициента динамической вязкости (
)
.
Далее по ходу решения необходимо подставить 5 значений времени в последнюю зависимость для , вычислить среднее значение 
из полученных
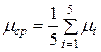
Подсчитать дисперсию 
по формуле
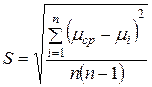(где 
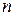= 5)
В заключение необходимо найти число и убедиться, что оно меньше единицы.
|
|
|
