Подобие потоков в случае преобладающего влияния сил давления

В этом случае условие частичного динамического подобия имеет вид

или

Критерий

называется числом Эйлера.

При изучении течений несжимаемой жидкости Eu не является определяющим, так как в качестве характерного давления вместо Р можно принять скоростной напор ρV²/2. Если статическое давление заменить разностью статических давлений ΔР в разных точках течения, то критерий Эйлера примет вид

.

В этом виде критерий Эйлера применяется при исследовании гидравлических сопротивлений в каналах как определяющий критерий. Например, один из аэродинамических коэффициентов

,

называемый коэффициент давления

В газовой динамике критерий Эйлера представляют с помощью выражений для скорости звука a² = kp/ρ и числа Маха M = V/a в следующем виде Eu = ¹/(kμ²). Следовательно, в газовой динамике вместо критерия Эйлера используются два других: показатель адиабаты k = Cp/Cv и число Маха M = V/a, которые характеризуют сжимаемость газа и в подобных течениях должны быть одинаковы.

Подобие в случае одновременного действия нескольких сил

При одновременном действии нескольких сил для обеспечения подобия необходимо, чтобы в натуре и на модели величины соответствующих критериев подобия были равны. Как правило, добиться этого бывает очень трудно или даже невозможно.

Задача 12.4. В каком соотношении должны находиться значения вязкости двух потоков различных жидкостей для того чтобы для обоих потоков числа Рейнольдса и Фруда были одинаковы?

Решение: Из Fr_H = Fr_M имеем

.

Подставляя соотношение для скорости в условие Re_H = Re_M получим

.

Если L_H > L_M, то необходимо, чтобы было ν_Н > ν_M. Например, если необходимо моделировать движение корабля в воде и модель выполнена в масштабе

то вместо воды должна быть взята жидкость вязкостью в тысячу раз меньше, чем вязкость воды, так как ν_М = (0,01)^3/2ν_Н = 0,001ν_Н. В настоящее время таких жидкостей нет и выполнение условия, поставленного в задаче возможно лишь при ограниченных различиях в линейных размерах модели и натуры.

Задача 12.5. При строительстве моста с промежуточными опорами они обычно вызывают подпор в водотоке (повышение уровня). Для уточнения этого подпора h_н проводилось моделирование в лабораторных условиях. Длина натуральной мостовой опоры l_н=20м, ширина её b_н=4,0м. Глубина воды в русле до устройства моста H_н=7,2м. средняя скорость течения воды υ_н=2,0м/с, расход воды в реке Q_н=1220м³/с. Исходя из возможностей лабораторного оборудования линейный масштаб был принят равным α_L=45(т.е. L_н/L_м=45). Определить длину и ширину опоры на модели, глубину потока на модели, расход воды в модельной установке и подпор.

Решение: находим линейные размеры модели. Длина опоры l_н=20/45=0,44м, ширина опоры b_н=4,0/45=0,088м, глубина потока на модели H_н=7,2/45=0,16м. необходимую скорость течения воды на модели находим исходя из равенства чисел Фруда на натуре и на модели или т.е. необходимый расход воды в модели

В результате опытов было установлено, что подпор на модели h_м=0,025м. В натуре подпор будет h_н=45^. h_м=1,125м.

 

Автомодельность

Если какая либо – величина, характеризующая гидравлическое явление не зависит от от какого – либо критерия подобия, то говорят, что она автомодельна по отношению к этому критерию. Например, коэффициент гидравлического сопротивления λ в квадратичной области и коэффициент Шези С не зависят от числа Рейнольдса и поэтому автомодельны по числу Re. При скорости течения газа не превышающих нескольких десятков метров в секунду сжимаемость можно не учитывать и такие течения мохно считать автомодельными по числу Маха. Существование областей автомодельности облегчает моделирование гидравлических явлений, так как делает ненужным удовлетворять некоторым критериям подобия.

Задача 12.6 Водосливная плотина в виде водослива практического профиля изучается в лаборатории на геометрически подобной модели, выполняемой в масштабе 1:25. Определить: 1. Напор над верхней частью пластины на модели, если в натуре он будет равен 4,5м;

2. Расход через плотину в натуре, если расход, полученный при испытании модели, равен

Решение: Так как коэффициент геометрического подобия по условию задачи равен 25, то напор равен

Так как движение через плотину происходит под действием силы тяжести, то моделирование необходимо производить по числу Фруда (вязкость воды можно не учитывать), поэтому и

и .

Кроме того,

.

Окончательно

 

Задача 12.7. Масло прокачивается в трубе диаметром , расход его равен Q. Необходимо определить расход воды в модельной установке- трубе диаметром при условии, что движение в обеих трубах должно быть гидродинамически подобным. Коэффициенты кинематической вязкости масла и воды равны соответственно

 

 

№ Варианта
Диаметр,
Расход, Q, л/с
Диаметр,

 

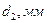
№ Варианта
Диаметр,
Расход, Q, л/с
Диаметр,

 

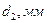
№ Варианта
Диаметр,
Расход, Q, л/с
Диаметр,

 

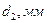
Задача 12.8. С помощью моделирования необходимо установить максимальное заглубление всасывающей трубы насоса под уровнем нефти в резервуаре с тем, чтобы не возникало воронки и не происходило засасывание воздуха.

Насос в натурной установке откачивает расход нефти Q, по трубе диаметром . Испытания производятся на геометрически подобной модели, линейный масштаб которой принят равным 1:n от натуры.

Так как условия входа нефти в трубу определяется в данном случае совместным влиянием свойств инертности, вязкости и весомости жидкости, при моделировании необходимо соблюдать равенство чисел Ренольдса и Фруда. В задаче требуется определить:

1. Какова должна быть вязкость жидкости, используемой на модели.

2. Каков должен быть для модели откачиваемый расход 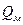и какая будет при этом скорость в трубе.

3. При какой глубине начнет образовываться воронка на натурной установке, если для модели эта величина оказалась равной .

Принять кинематический коэффициент вязкости нефти равным 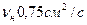. В качестве модельной жидкости можно принять раствор глицерина в воде, меняющий вязкость от до в зависимости от соотношения глицерина и воды.

 

№ варианта
Расход,
Диаметр,
Коэффициент Подобия, n
Глубина,

 

 

№ варианта
Расход,
Диаметр,
Коэффициент Подобия, n
Глубина,

 

 

№ варианта
Расход,
Диаметр,
Коэффициент Подобия, n
Глубина,

 

Задача 12.9.

Истечение керосина (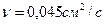) через отверстие диаметром d моделируется на воде () при соблюдении вязкого и гравитационного подобия.

Определить:

1. Диаметр отверстия для модели

1. В каком отношении должны находиться высоты уравнений для натуры и для модели .
2. В каком отношении при выполнении этих условий будут находиться расходы Q и .

 

№ варианта
Диаметр,

 

№ варианта
Диаметр,

Задачи.

1. В каком отношении находятся числа Ренольдса для двух потоков одинаковой жидкости при соблюдении гравитационного подобия.

2. Рассчитать тягу дымовой трубы у которой плотность газов изменяется по высоте (температура газов уменьшается с высотой линейно).

3. 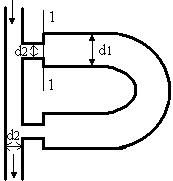В качестве нагревательных приборов системы отопления использованы стальные трубы =0,1м. Подводящие и соединительные линии выполнены из труб =0,025м и приварены к концам нагревательных труб. Определить потери давления при внезапном расширении трубопровода в сечении 1-1, если скорость течения горячей воды в подводящих линиях , а температура воды .

4. Вентиляционная труба d =0,1м (100мм) имеет длину l =100м. Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе, Давление на выходе Местных сопротивлений по пути не имеется. Температура воздуха .

5. Для измерения падения давления в вентиляционной трубе применяется чашечный наклонный микроманометр, наполненный спиртом удельного веса Наклон трубки . Определить необходимую длину l манометрической шкалы для измерения падения давления .

6. Кессон П- образного сечения в начале работ по выемке грунта покоится на дне реки LM, сильно пропускающем воду, на глубине Н =200м от поверхности воды. Как велико должно быть давление р сжатого воздуха в рабочей камере К, для того чтобы вода не просачивалась через речное дно?

7. Считая температуру газа постоянной, установить, как будет изменяться его кинематическая вязкость при увеличении давления.

8. Доказать, что при изотермическом течении газа по трубе постоянного сечения коэффициент сопротивления не меняется по длине газопровода.

9. Вентиляционный короб имеет квадратное сечение со стороной а=0,5м и длину L=40м. Определить перепад давления ΔН в коробе в мм.водяного столба при средней скорости воздуха , температуре . ().

10. По трубопроводу переменного сечения перемещается воздух. Считая процесс адиабатическим, определить температуру воздуха в сечении 2-2, если скорость в сечении 1-1 , а в сечении 2-2 , температура .

11. Найти потери давления при трении, приходящегося на 1м бетонной трубы диаметром d=1м (), если по ней транспортируется воздух с расходом , плотностью и кинематической вязкостью .

12. Определить необходимое давление в начале магистрального стального газопровода диаметром d=300мм для транспортирования 20000 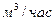газа с удельным весом . Длина трубопровода L=2000м, , а конечное давление в магистрали .

13. Давление в баллоне кислородом для газовой сварки при расположении его на улице, где температура , равно . Каково будет давление в баллоне при внесении его в помещение с температурой .

14. Через поперечное сечение трубопровода за 1 сек проходит воздух объемом 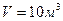при температуре Т=300К и давлении . Чему равен массовый расход воздуха?

15. Определить расход и скорость истечения воздуха из резервуара через отверстие диаметром d=20мм, если воздух в резервуаре находится под давлением при температуре , а истечение происходит в атмосферу ().

16. Определить плотность воздуха при избыточном давлении р=4900Па и температуре t=200 .

17. Для измерения падения давления в вентиляционной трубе применяется чашечный накленный микроманометр, в котором в качестве рабочей жидкости используется спирт плотностью . Наклон трубки . Определить необходимую длину l манометрической шкалы для измерения падения давления .

18. 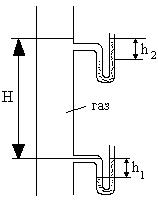Избыточный напор газа на первом этаже дома составляет . Определить избыточный напор газа на высоте Н=42м, считая плотность газа и воздуха неизменными. Плотность газа , воздуха .

 

 

19. Барометр, установленный на третьем этаже многоэтажного дома показывает давление, соответствующее h=730мм.рт.ст. Каково будет показание барометра после переноса его на 15 этаж, если высота каждого этажа от пола до пола 4,2м, а температура воздуха 20 .

 

Литература

1. Альтшуль А. Д., Киселев П. Г. Гидравлика и аэродинамика. Основы механики жидкости: Учеб. Пособие для вузов. Изд. 2-е, перераб. и доп. М.:Стройиздат, 1975. 323 с.

2. Киселев П. Г. Гидравлика: Основы механики жидкости: Учеб. Пособие для вузов М.:Энергия, 1980.360 с.

3. Учинчус А. А. Гидравлика и гидравлические машины. Харьков, 1966. 399 с.

4. Штеренлихт Д. В. Гидравлика: Учебник для вузов. М.: Наука, 1984. 640 с.

5. Смыслов В. В. Гидравлика и аэродинамика: Учебник для вузов. Киев: Вища школа, 1979. 336с.

6. Федяевский К. К., Войткунский Я. И.,Фадеев Ф. И. Гидромеханика. М.:Судостроение, 1968. 568 с.

7. Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. 2-е изд. Перераб. М.: Машиностроение, 1982. 423с.

8. Калицун В.И., Дроздов Е.В. Основы гидравлики и аэродинамики.-М.:Стройиздат, 1980-247с.

9. Сборник задач по машиностроите6льной гидравлике. Бутаев Д.А., Колмынова З.А., Подводз Л. Г и др.М., «Машиностроение», 1972,472с.

10. Ерохин В.Г., Маханько М.Г. Сборник задач по основам гидравлики и теплотехники. М.: -Энергия, 1979.-240с.

11. Примеры расчетов по гидравлике. Учебное пособие для вузов. Под ред. А.Д. Альтшуля. М., Стройиздат, 1976, 255с. Авт.: А.Д.Альтшуль, В.И. Калицун, Ф.Г. Майрановский, П.П. Польгунов.

12. Смыслов В.В. Гидравлика и аэродинамика. Учебник для вузов.-Киев:Вищашкола. 1979.-336с.

13. Яблонский В.С. Сборник задач и упражнений по технической гидравлике/В.С. Яблонский, И.А. Исаев. М.: Физматчиз, 1963, 200с.

14. Калякин А.М. Гидравлические расчеты трубопроводов. Истечение жидкости через отверстия и насадки. Конспект лекций по курсу «Гидравлика»/А.М Калякин, Саратов, СГТУ, 2004-56с.

 

⇐ Предыдущая6789101112131415

Поделиться:

Воспользуйтесь поиском по сайту: