 |
Понятие точечно-векторного аффинного n-мерного пространства
|
|
|
|
Историческая справка
Многомерная геометрия – геометрия пространств размерности, больше трёх. Термин «многомерная геометрия» применяется к тем пространствам, геометрия которых была первоначально развита для случая трёх измерений и только потом обобщена на число измерений n > 3, то есть, прежде всего к евклидову пространству, а также к пространствам Лобачевского, Римана, проективному, аффинному (общие же римановы и другие пространства были определены сразу для n-измерений). Разделения трёх- и многомерной геометрий имеет историческое и учебное значение, так как задачи ставятся и решаются для любого числа измерений, когда и поскольку это осмысленно. Построение геометрии указанных пространств для n-измерений проводится по аналогии со случаем трёх измерений. При этом можно исходить из обобщения непосредственно геометрических оснований 3-мерной геометрии, из той или иной системы её аксиом или из обобщения её аналитической геометрии, перенося её основные выводы со случая трёх координат на произвольное n.
Именно так и начиналось построение n-мерной евклидовой геометрии. В настоящее время предпочитают исходные из понятия векторного пространства.
Исторически представление в более чем 3-мерном пространстве зарождалась постепенно; первоначально – на почве геометрического представления степеней: а 2 – «квадрат», а 3 – «куб», а 4 – «биквадрат», а 5 – «кубоквадрат» и т. д. (ещё у Диофанта в 3 в. и далее у ряда средневековых авторов). Мысль в многомерном пространстве выражал И. Кант (1746), а о присоединении к пространству в качестве 4-й координаты времени писал Ж. Д’Аламбер (1764). Построение же евклидовой моногомерной геометрии было осуществлено А. Кэли (1843), Г. Грассманом (1844) и Л. Шлефли (1852). Первоначальные сомнения и мистика, связанные со смешением этих обобщений с физическим пространством, были преодолены, и n-мерное пространство как плодотворное формально-математическое понятие скоро полностью укрепилось в математике.
|
|
|
Многомерные пространства возникли путём обобщения, аналогии с геометрией на плоскости и в трёхмерном пространстве. На плоскости каждая точка задаётся в системе координат двумя числами – координатами этой точки, а в пространстве – тремя координатами. В n-мерном же пространстве, точка задаётся n координатами, то есть записывается в виде A (x 1, x 2,..., x n), где x 1, x 2,..., x n – произвольные действительные числа (координаты точки А). На плоскости система координат имеет две оси, в пространстве – три, а в n-мерном пространстве система координат содержит n осей, причём каждые две из этих осей перпендикулярны друг другу. Конечно, такие пространства существуют лишь в воображении математиков и тех специалистов из других областей из других областей знания, которые применяют эти математические абстракции. Ведь реальное пространство, в котором мы живём, математически хорошо описывается трёхмерным пространством (евклидовым или римановым, но именно трёхмерным). Увидеть – в буквальном, физическом смысле этого слова – фигуры в четырёхмерном пространстве (а тем более в пространствах большего числа измерений) не в состоянии никто, даже самый гениальный математик; их можно видеть только мысленным взором.
Существуют различные парадоксы четвёртого измерения. Если, например, на плоскости имеется кольцо (оболочка), а внутри – кружок, то как бы мы ни двигали этот кружок по плоскости, вынуть его из этой оболочки, не разрывая её, невозможно. Но стоит только выйти в третье измерение, и кружок легко вынуть из кольца, подняв его вверх, над плоскостью, то, не прорывая оболочку, невозможно вынуть из неё этот шарик. Но если бы существовало четвёртое измерение, то можно было бы «поднять» шарик над трёхмерным пространством в направлении четвёртого измерения, а затем положить его снова в трёхмерное пространство, но уже вне оболочки. И то, что это сделать никому не удаётся, приводят как довод против существования четвёртого измерения. Довод ошибочен, так как в нём спутаны два вопроса.
|
|
|
Первый вопрос: имеется ли в реальном? Ответ на этот вопрос отрицателен.
Второй вопрос: можно ли рассматривать четырёхмерное пространство абстрактно, математически? Ответ утвердителен.
Нет ничего нелогичного или противоречивого в том, чтобы рассматривать четвёрки чисел (x 1, x 2, x 3, x 4), исследовать свойства этих «четырёхмерных точек», составлять из них фигуры, доказывать теоремы, постоянно строя таким образом, геометрию четырехмерного (или, вообще n-мерного) пространства. Но математическая н6епротиворечивость n-мерной геометрии ещё недостаточна для суждения о ценности этой теории.
§ 2. Понятие векторного многомерного пространства на основе аксиоматики Вейля.
В векторной аксиоматике понятие вектора является одним из основных (необходимых) понятий. Понятие числа тоже будем считать основным понятием и исходить из того, что теория действительного числа известна. Свойства операций сложения векторов и умножения вектора на действительные числа примем за аксиомы. Тогда можно дать аксиоматическое определение векторного пространства.
Пусть V – некоторое непустое множество, элементы которого будем называть векторами, и которые могут быть произвольной природы, R – множество действительных чисел. Введём для векторов операции сложения векторов и умножения вектора на действительные числа из R такие, чтоа) любым двум векторам a и b поставлен в соответствие определённый вектор, называемый суммой и обозначаемый a+b;б) любому вектору a и любому действительному числу α поставлен в соответствие определённый вектор, называемый произведением вектора на число и обозначаемый через αа. И пусть при этом выполняются следующие свойства аксиомы:1. a+b=b+a для любых векторов a и b из V;2. (a+b) +с=a+ (b+c), для любых векторов a, b, c  V. 3. Существует такой вектор О
V. 3. Существует такой вектор О  V, что а+О=а;4. Для любого вектора а
V, что а+О=а;4. Для любого вектора а  V существует такой вектор – a
V существует такой вектор – a  V, что а+(- а)=O;5.
V, что а+(- а)=O;5. 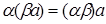 для любых чисел
для любых чисел  и
и 
 V;6.
V;6. 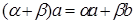 для любого числа
для любого числа 
 R и любых векторов a и b из V;7. 1· а = а для любого вектора а
R и любых векторов a и b из V;7. 1· а = а для любого вектора а  V.
V.
|
|
|
Тогда множество V называется действительным линейным векторным пространством или векторным пространством. Введённое определение не накладывает никаких ограничений на природу элементов множества V, поэтому могут существовать различные векторные пространства.
Примеры: Векторное пространство V 1 – множество векторов на прямой; Векторное пространство V 2 – множество векторов на плоскости; Векторное пространство V 3 – множество векторов пространства трёх измерений; Множество различных многочленов от одной переменной также составляет векторное пространство. «Векторами» являются многочлены. Используя утверждения, что в обычном пространстве трёх измерений существует три линейно независимых вектора, то есть выполняется равенство:
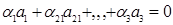 , когда
, когда  ;
;
Любая система, состоящая более, чем из 3-х векторов этого пространства, линейно зависима.
Продолжая строить аксиоматическую теорию векторных пространств, введём следующее определение.
Определение: Векторное пространство V называется n-мерным, если в нём выполняются аксиомы:
9. В векторном пространстве V существуют n линейно независимых векторов.
10. Любая система, состоящая более, чем из n векторов пространства V, линейно зависима.
Число n называется размерностью векторного пространства и обозначается символом dim V, а само пространство будем обозначать символом V n. Базисом n -мерного векторного пространства V n называется любая упорядоченная система векторов, таких, что система линейно независима; любой вектор пространства V n является линейной комбинацией данной системы векторов. Базис не может иметь более трёх векторов и менее чем три вектора. Очевидно, что базис пространства V 3 будем называть 3-мерным и обозначать В = (е 1, е 2, е 3), где векторы е 1, е 2, е 3 называются базисными. Из аксиом 9 и 10 следует, что в n-мерном векторном пространстве V n существует хотя бы один базис, состоящий из n векторов. Можно доказать, что в V n существует бесчисленное множество базисов и любой из них состоит из n векторов. N -мерный базис будем обозначать В = (е 1, е 2,…, е n), а векторы е 1, е 2,…, е n называть базисными. Следствие: Любая система, состоящая более чем из трёх векторов обычного пространства трёх измерений, линейно зависима.
|
|
|
§ 3. Евклидово векторное пространство
Строя аксиоматическую теорию аналитической геометрии на векторной основе, введём следующее определение.
Определение 1: Скалярным произведением на векторном пространстве V называется операция, которая любой паре векторов a и b ставит в соответствие некоторое действительное число, обозначаем символом a b и обладающее следующими свойствами:11. Для любых векторов a, b  V и любого вектора a b = b а;12. Для любых двух векторов a, b
V и любого вектора a b = b а;12. Для любых двух векторов a, b  V и любого числа
V и любого числа 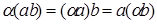 .13. Для любых трёх векторов a, b, c
.13. Для любых трёх векторов a, b, c  V
V  ;14. Для любого ненулевого вектора а
;14. Для любого ненулевого вектора а  V aa >0.
V aa >0.
Определение 2: Векторное пространство V n, в котором введена операция скалярного произведения векторов, удовлетворяющая аксиомам 11-14, называется евклидовым векторным пространством. Будем обозначать его символом Е n.
На основе определения 1 можно ввести понятие длины вектора и величины угла между векторами.
Число аа называется скалярным квадратом вектора а и обозначается а 2. Из аксиомы 14 следует, что а 2>0, следовательно, 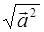 - действительное положительное число. Оно называется длиной или нормой вектора и обозначается:
- действительное положительное число. Оно называется длиной или нормой вектора и обозначается: 
 . Если
. Если  1, то вектор а называется единичным.
1, то вектор а называется единичным.
На основе аксиом 11-14 можно указать следующие утверждения: Для любых векторов a, b 1, b 2,…, b n выполняется равенство
 .
.
 , где а – произвольный вектор;
, где а – произвольный вектор;
Если  , то
, то  , а если
, а если 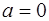 , то
, то  ;Если
;Если  , то
, то 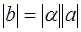 .
.
Можно показать, что если  , то вектор
, то вектор 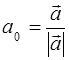 является единичным, его называют ортом вектора а. Он определяет то же направление, что и вектор а.
является единичным, его называют ортом вектора а. Он определяет то же направление, что и вектор а.
При решении метрических задач, т. е. задач, связанных с измерением длин векторов и величин углов, пользуются ортонормированным базисом.
Определение: Базис называется ортонормированным, если все его векторы единичные и попарно ортогональны, т. е. если 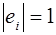 и
и  (
( ) при
) при 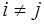 .
.
Теорема. В евклидовом пространстве Е n существуют ортонормированные базисы.
Действительно, если (а 1, а 2,…, а n) – ортогональный базис, то можно рассмотреть векторы
 ,
, 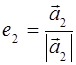 ,…,
,…,  .
.
Ясно, что базис (е 1, е 2,…, е n) ортонормированный, так как его векторы единичные и попарно ортогональны.
Введём обозначения: В =(i, j) или B=(i, j, k) – ортонормированные базисы евклидовых векторных пространств Е 2 и Е 3 соответственно.
Понятие точечно-векторного аффинного n-мерного пространства
|
|
|
В § 2 и § 3 были аксиоматически определены различные векторные пространства: линейные векторные, n-мерные векторные, евклидовы векторные. Но для построения геометрии, то есть для рассмотрения различных геометрических фигур, одних векторов недостаточно, нужны ещё точки.
Аксиоматизируя построение вектора по двум точкам, введём следующее определение.
Определение. Аффинным пространством называют некоторое множество А* элементов произвольной природы, называемых точками, для которого задано
а) некоторое векторное пространство V;
б) отображение, которое любым двум точкам А и В  А * ставит в соответствие некоторый вектор из V, обозначаемый АВ.
А * ставит в соответствие некоторый вектор из V, обозначаемый АВ.
При этом требуется выполнение следующих аксиом:
15. Для любой точки А 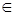 А * и любого вектора А из V существует единственная точка В
А * и любого вектора А из V существует единственная точка В 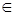 А* и любого вектора а
А* и любого вектора а 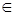 V существует единственная точка В
V существует единственная точка В 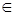 А *, такая что АВ = а.
А *, такая что АВ = а.
16. Для любых трёх точек А, В, С 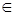 A * имеет место равенство АВ + ВС = АС.
A * имеет место равенство АВ + ВС = АС.
Аксиома 15 называется аксиомой откладывания вектора от точки, а аксиома 16 – аксиомой треугольника, из которой следует правило треугольника и правило параллелограмма сложения векторов.
Размерность пространства V называется размерностью соответствующего аффинного пространства А * и обозначается символом А *n.
Отметим некоторые важные следствия из аксиом 15-16.
При любом выборе точки А вектор АА нулевой.
Если АВ =0, то точки А и В совпадают.
Для любых точек А и В АВ = - ВА.
Если АВ=С D, то АС=В D.
Для произвольных точек А 1, А 2,…, А n выполняется равенство А 1 А 2+ А 2 А 3+ А n-1 А n= А 1 А n (правило многоугольника сложения векторов).
Пространство А*n содержит бесчисленное множество точек.На основе аксиом 1-10 и 15-16 аффинной геометрии нельзя ввести понятий длин отрезков и величин (мер) углов. Эти понятия можно ввести, используя скалярное произведение векторов.
Как известно, введение в V n скалярного произведения векторов приводит к евклидову векторному пространству Е n.
Определение. Аффинное пространство А n*, в котором соответствующее ему векторное пространство V n превращено в евклидово векторное пространство Е n, называется евклидовым n-мерным пространством.
Для этого пространства введём обозначение Е n. Согласно определению ясно, что всякое аффинное пространство А n* можно превратить в евклидово пространство Е n, задавая на векторном пространстве V n скалярное произведение векторов, удовлетворяющее аксиомам 11-14 (§ 3).
Таким образом, в Е n выполняются аксиомы 1-16.
На основе аксиом евклидова пространства строится евклидова геометрия.
В евклидовой геометрии, очевидно, справедлива вся изложенная выше теория аффинной геометрии. Но пространство Е n обладает метрическими свойствами, которые следуют из аксиом скалярного произведения векторов и связаны с измерением длин отрезков и мер углов. Поэтому евклидову геометрию называют ещё метрической геометрией.
Метрические аксиомы позволяют установить метрику евклидова пространства, т. е. расстояния между его точками. Определим сначала модуль |a| вектора а как неотрицательный корень из его квадрата, т. е.
 (4.1)
(4.1)
Векторы, модуль которых равен 1, будем называть единичными векторами; единичный вектор 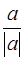 будем обозначать а 0.
будем обозначать а 0.
Будем считать расстоянием между точками А и В модуль вектора АВ; будем обозначать это расстоянием АВ.
Таким образом, расстояние АВ между точками А (х) и В (y) определяется соотношением
 (4.2)
(4.2)
Из определения расстояния следует, что
Расстояние симметрично, т. е.
АВ = ВА (4.3)
Расстояние позитивно, т. е. (4.4) AB ≥ 0, причём знак равно имеет место только при совпадении точек А и В. Покажем, что для расстояний между точками евклидова пространства помимо свойств 1 и 2 выполняется также «неравенство треугольника».расстояние между всякими двумя точками не более суммы расстояний между этими точками и третьей точкой, т. е.
АС ≤ АВ + ВС (4.5)
Множество точек, для всяких двух точек А и В которого определено число АВ, удовлетворяющего условиям 1-3, называется метрическим пространством. Для доказательства неравенства треугольника докажем так называемое неравенство Коши
 (4.6)
(4.6)
Скалярный квадрат вектора a – tb неотрицателен при любом вещественном t
 , т. е.
, т. е. 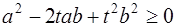 .
.
В случае b = 0 обе части неравенства (4.6) равны 0, т. е. неравенство выполняется автоматически.
Если 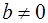 , получим
, получим  .
.
Тогда неравенство примет вид
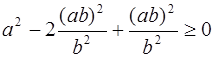 , т. е.
, т. е.  ,
,
что равносильно неравенству (4.6). Рассмотрим три точки А (х), В (у) и С (z). Тогда 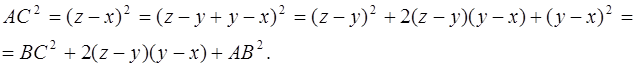
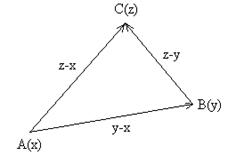 Рис. 1
Рис. 1
Но в силу неравенства Коши 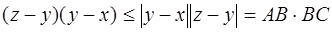 . Поэтому
. Поэтому  , откуда получаем неравенство (4.5).
, откуда получаем неравенство (4.5).
Глава II. Многомерные геометрические образы в n-мерных пространствах
|
|
|


