 |
Геометрия k-плоскостей в аффинном и евклидовом пространствах
|
|
|
|
Определение k -плоскости
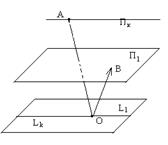
Пусть в n-мерном аффинном пространстве U n зафиксирована произвольная точка А, и в соответствующем линейном пространстве L n зафиксировано произвольное k-мерное подпространство L k.
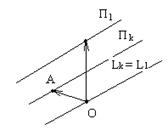
Определение. Множество всех точек М аффинного пространства, для которых АМ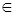 
L k, называют k-мерной плоскостью, проходящей через точку А в направлении подпространством Lk.
Рис. 11, где k = 2
Говорят также, что L k есть направляющее подпространство этой плоскости. Очевидно, что каждая плоскость определяет однозначно своё направляющее пространство.
Точку М называют текущей точкой плоскости. На рисунке показаны три положения М 1, М 2, М 3 текущей точки М.
Частные случаи k-плоскостей
Если k = 0, то плоскость состоит из одной точки А. Поэтому каждую точку аффинного пространства можно рассматривать как нуль-мерную плоскость.
Одномерная плоскость называется прямой линией.
Плоскость размерности n – 1 называется гиперплоскостью.
При k = n плоскость совпадает со всем пространством U n.
В определении плоскости выделена точка А. Докажем, что в действительности все точки плоскости равноправны.
Обозначим плоскость через П k и зафиксируем произвольную точку В 
. Надо доказать, что точка М принадлежит плоскости П k тогда и только тогда, когда 
(т. е. что любая точка М может играть роль А).
Пусть 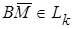. По определению плоскости 
. Отсюда и по определению подпространства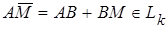 
, поэтому 
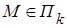. Обратно, если 
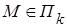, то 
следовательно, 
.
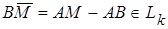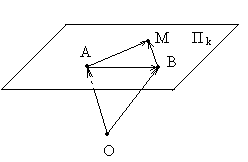
Рис. 12
Теорема. Всякая k-мерная плоскость в аффинном пространстве сама является k-мерным аффинным пространством.
Доказательство. Пусть дано аффинное пространство U, которому соответствует линейное пространство L, пусть П k – плоскость, проходящая через точку А в направлении подпространства L k. Возьмём в плоскости П k две произвольные точки M, N. По определению аффинного пространства им соответствует вектор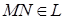 
. По определению плоскости векторы АМ и А N принадлежат подпространству L k.
|
|
|
Следовательно,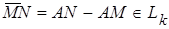 
. Таким образом, каждой упорядоченной паре точек М, N плоскости Пk, поставим в соответствие вектор MN из k-мерного пространства L k. При этом соблюдаются для П k аксиомы, вытекающие из определения k-мерной плоскости и для всего аффинного пространства U. Теорема доказана.
Замечание. Если плоскость проходит через начало аффинной системы координат в направлении подпространства L k, то совокупность радиус-векторов её точек образует подпространство, по определению совпадающее с подпространством L k.
Пусть в аффинном пространстве U даны точки А 0, А 1,…, А k (в числе k + 1). Эти точки находятся в общем положении, если они не принадлежат ни одной (k –1)-мерной плоскости.
Проверим, что точки А 0, А 1,…, А k находятся в общем положении тогда и только тогда, когда векторы А 0 А 1,…, А 0 А k линейно независимы (рис. 13), причём безразлично, какую из точек брать в качестве А 0 (то есть за начало векторов, идущих из неё в другие точки).
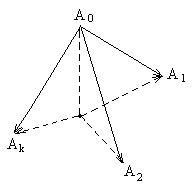
Рис. 13
Из сказанного в этом пункте и из определения плоскости следует, что через систему точек А 0, А 1,…, А k, находящихся в общем положении, проходит k-мерная плоскость и притом только одна.
Предположим, что в пространстве U n зафиксирована какая-нибудь аффинная система координат с началом О и базисом е 1, е 2, …, е n. Рассмотрим плоскость П k, проходящую через точку А в направлении подпространства L k.
Будем считать, что точка А имеет координаты р 1, р 2, …, р n и что L k задаётся как независимая система векторов q 1, q 2, …, q k. Тогда радиус-вектор ОМ текущей точки плоскости можно записать в виде
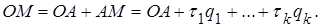(6. 1)
где параметры τ 1, τ 2, …, τ k независимо друг от друга пробегают всевозможные числовые значения, а вектор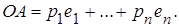 
(рис. 14)
|
|
|
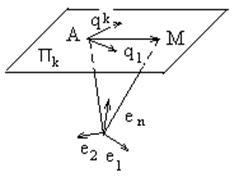Рис. 14
Разложим вектор q 1, q 2, …, q k по базису е 1, е 2, …, е n:
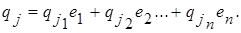
Координаты текущей точки М обозначим, как обычно, через (x 1, x 2, …, x n) и запишем векторное равенство в координатах. В результате получим n числовых равенств.
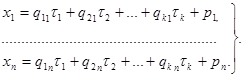(6. 2)
Эти равенства называются параметрическими уравнениями плоскости П k.
Пример. Пространство, изучаемое в стереометрии, является трёхмерным аффинным пространством. В нём одномерные и двумерные плоскости совпадают соответственно с прямыми линиями и плоскостями, понимаемыми в элементарно-геометрическом смысле. В отличие от пространства, изучаемого в элементарной геометрии, в аффинном пространстве не определены метрические понятия: расстояния между точками и длины линий, площади и объёмы фигур, углы и перпендикулярность. При исследовании фигур в аффинном пространстве изучаются лишь те геометрические свойства, которые не зависят от метрических понятий.
2. Уравнения k-плоскости по k+1 точкам
Если заданы k+1 точек А 0(х 0), А 1(х 1), …, А n(х n) и векторы А 0 Аа = ха – х 0 независимы, то эти точки определяют единственную k – плоскость, проходящую через них: в этом случае за направляющие векторы этой плоскости можно принять векторы А 0 Аа и векторное уравнение k-плоскости можно записать в виде
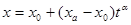(6. 3)
Будем называть k-плоскость, определяемую точками А 0(х 0), А 1(х 1), …, А n(х n), k-плоскостью А 0, А 1, …, А k.
Случай k = n-1
В дальнейшем будем часто иметь дело с k-поверхностями и k-плоскостями при k = n – 1. Говоря, «поверхность n-пространства» и «плоскость n-пространства», но иметь в виду (n – 1)-поверхность и (n – 1)-плоскость этого пространства. Часто поверхность и плоскость называется соответственно гиперповерхностью и гиперплоскостью.
Поверхность можно задать одним координатным уравнением
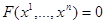(6. 4)
если координаты xi, удовлетворяющие этому уравнению, можно представить как функции n – 1 параметров t 1, t 2, …, t n-1, то получим
F (x) = 0. (6. 5)
3. Взаимное расположение плоскостей
3. 1 Пересекающиеся плоскости
Во всём этом пункте размерности плоскостей и подпространств обозначены индексами снизу. Пусть две плоскости П k и П l пересекаются, то их пересечением является некоторая плоскость П m.
|
|
|
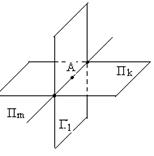k = l = 2, m = 1 Рис. 15
Замечание 1. Не исключена возможность, что П m состоит из одной точки (m = 0). Это видно на примере двух пересекающихся прямых или прямой и плоскости (рис. 16).
Рис. 16
В общем случае по одной точке могут пересекаться две плоскости, сумма разностей которых не превышает размерности пространства, например, двумерные плоскости в четырёхмерном пространстве.
Замечание 2. Не исключено и другое, когда одна из двух плоскостей целиком принадлежит другой. Например,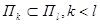 
, тогда 
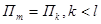(рис. 17)
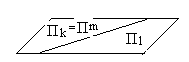k = m = 1, l = 2
Рис. 17
2) Если плоскости П k и П l пересекаются по плоскости П m, то существует единственная плоскость П r, размерности r = k + l – m, содержащая П k и П l, причём ни в какой плоскости меньшей размерности П k и П l не могут одновременно поместиться. Направляющее подпространство L r плоскости П r является суммой направляющих подпространств L k и L l. Эта сумма является прямой суммой тогда и только тогда, когда П k и П l пересекаются по одной точке (m = 0, см. рис. 18).
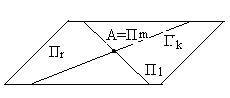
Рис. 18
В частном случае, когда n = k + l – m, роль плоскости П r выполняет всё пространство U n (при r = n = 3 см. рис. 15).
3) Если пересекающиеся плоскости П k и П l содержатся в какой-нибудь плоскости П r, то размерность их пересечения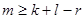 
. В частности, 
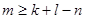для любых двух непересекающихся плоскостей из U n.
4) Если плоскости П k и П l проходят через точку А в направлении подпространств L k и L l соответственно и если L k содержится в L l, то плоскость П k содержится в плоскости П l. Если при этом k = l, то П k совпадает с П l (также и L k совпадает с L l).
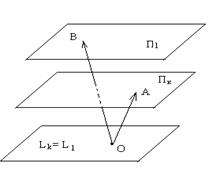
Параллельные плоскости
Пусть теперь плоскость П k определяется точкой А и подпространством L k, а плоскость П l – точкой В и подпространством L l. Будем считать, что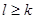 
.
Определение: Плоскость П k параллельна плоскости П l, если 
.
В этом случае плоскость П l параллельна плоскости П k.
Замечание 1. Согласно этому определению включение 
является частным случаем параллельности.
Замечание 2. Если П k параллельна П l, причём k = l, то L k совпадает с L l.
Замечание 3. Убедимся, что при n = 3 частные случаи k = l = 1,
|
|
|
k = l = 2 и k = 1, l = 2 согласуются с понятием параллельности прямых и плоскостей, известным из элементарной геометрии (рис. 19)
а) б) в)
Рис. 19
Пусть в произвольной аффинной системе координат две плоскости П и П l одинаковой размерности заданы системами линейных уравнений. Пользуясь определением параллельности, нетрудно установить следующее утверждение.
Утверждение. Для того, чтобы П и П’ были параллельными, необходимо и достаточно, чтобы соответствующие однородные системы уравнений были эквивалентны.
В частности, две гиперплоскости параллельны тогда и только тогда, когда в одних и тех же координатах они задаются уравнениями
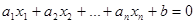и (6. 6)
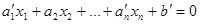(6. 7)
с пропорциональными коэффициентами при переменных:
.
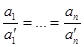Теорема 1. Пусть в аффинном пространстве U n даны плоскость П k и точка В. Тогда существует единственная плоскость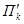 
размерности k, проходящая через точку В параллельно П k. Если 
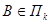, то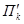 
совпадает с П k; если точка В расположена вне П k, то плоскости П k и 
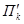не пересекаются.
Скрещивающиеся плоскости
Определение. Две плоскости называются скрещивающимися, если они не пересекаются и не параллельны.
Известно, что в трёхмерном пространстве U 3 две прямые линии, т. е. одномерные плоскости, могут скрещиваться, тогда как прямая линия и двумерная плоскость в U 3 скрещиваться не могут. С повышением размерности пространства оно становится более просторным, в результате чего появляется возможность строить в нём скрещивающиеся плоскости разных размерностей, а не только одномерные. Ниже сформулирована теорема 2, содержание которой можно рассматривать как общий приём построения скрещивающихся плоскостей. Именно, пусть в аффинном пространстве U n дана плоскость П l (l < n). Возьмём произвольную плоскость П k так, чтобы П k и П l не были параллельны и пересекались; плоскость, по которой они пересекаются, обозначим через П m. Пусть П r - плоскость наименьшей размерности, содержащая П k и П l. Мы знаем, что r = k + l – m.
Теорема 2. Если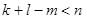 
, то всякая k-мерная плоскость, которая параллельна П k и не лежит в П r, скрещивается с П l.
Следствие. Если целые числа k, l, m, n удовлетворяют неравенствам
, 
, 
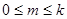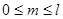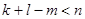, то в U n найдутся скрещивающиеся плоскости П k и П l с направляющими подпространствами L k и L l, пересечение которых 
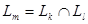имеет размерность m.
Доказательство теоремы 2. Так как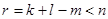 
, то плоскость П r не исчерпывает собой всего пространства U n. Это позволяет взять (с большим произволом) точку С, не лежащую в П r. Обозначим через 
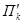плоскость размерности k, проходящую через точку С, параллельно П k. Ясно, что 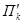не содержится в П r и что, выбирая по-разному точку С, мы можем получить любую k-мерную плоскость, удовлетворяющую условию теоремы. (См. рис. 14, на котором k = l = 2, r = 2, n = 4, и трёхмерные плоскости условно изображены в виде параллелепипеда).
|
|
|
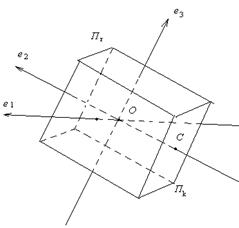
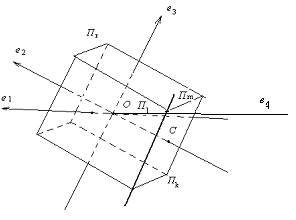
Рис. 20
Докажем, что плоскости П l и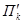 
скрещиваются. Заметим, что плоскость 
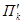не параллельна П l, так как в противном случае 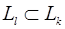или 
, или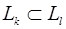 
, что противоречит условию расположения плоскостей П k и П l.
Теперь докажем, что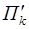 
и П l не пересекаются. Проведём через точку С вспомогательную r-мерную плоскость 
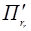, параллельную П r. Тогда 
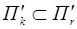и поэтому П k не может пересечь П l ибо в противном случае точка их пересечения 
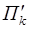принадлежала бы параллельным плоскостям П r и 
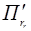. Следовательно, скрещивается с П l. Теорема 2 доказана.
Пусть в n-мерном аффинном пространстве U n даны скрещивающиеся плоскости П k и П l с направляющими подпространствами L k и L l, причём
, 
.
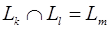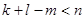Теорема 3. Существует единственная плоскость П r+1 размерности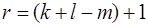 
, содержащая плоскости П k и П l.
Доказательство. Возьмём произвольную точку 
и зафиксируем произвольную точку 
; обозначим через 
линейную оболочку вектора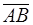 
(рис. 16). Допустим, что существует какая-то плоскость 
, содержащая П k и П l; пусть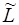 
- её направляющее подпространство. Очевидно, что 
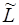должно содержать Lk, Llи 
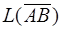, а следовательно, и сумму этих подпространств. Обозначим эту сумму через L r+1:
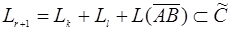
Обратно, если 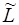- любое подпространство, включающее L r+1, то 
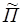, проходящая через точку А в направлении 
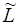, будет содержать П k и П l. В самом деле, так как 
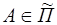и 
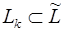, то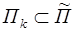 
; так как 
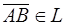, то 
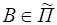, так как 
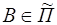и 
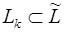, то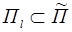 
.
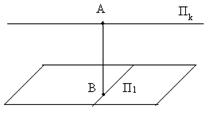
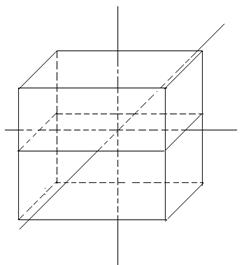
Рис. 21
Получим среди всех плоскостей искомую плоскость П r+1 минимальной размерности r + 1 в том единственном случае, когда в качестве берётся L r+1. Подсчитаем r + 1. С этой целью рассмотрим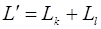 
и обозначим размерность 
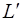через р. По теореме 3 (в n-мерном пространстве L имеются подпространства L k и L l, размерности которых соответственно равны k и l. Если их пересечение имеет размерность m, то размерность их суммы L k + L l равна r = k + l – m) имеем р = k + l – m.
Покажем, что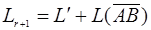 
есть прямая сумма, поэтому размерность L r+1 равна р + 1, то есть (r + 1) = (k + l – m) +1.
Для этого достаточно показать, что вектор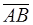 
не принадлежит пространству 
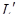. Предположим противное. Пусть 
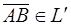. Тогда по определению суммы подпространств существуют векторы х и у такие, что 
, 
, 
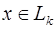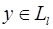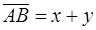. (v) По первой аксиоме аффинного пространства найдётся точка С такая, что 
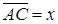, причём 
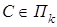. По второй аксиоме аффинного пространства 
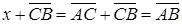. (vv)
Учитывая (v), (vv), находим, что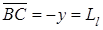 
, так что 
. Получается, что плоскости П k и П l имеют общую точку С, но это невозможно, поскольку плоскости П k и П l скрещиваются. Теорема 3 доказана.
Замечание. Рисунок 20 лишь частично иллюстрирует теорему 3. Например, если размерности П k и П l больше m и различны между собой,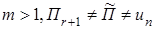 
, то, как, 
Проведённые выше рассуждения показывают, что плоскости П k и П l, о которых идёт речь в теореме 3, не содержатся ни в какой плоскости меньшей размерности, чем r + 1.
Сохраняя обозначения предыдущего подпункта, сформулируем достаточное условие пересечения двух плоскостей.
Теорема 4. Если в U n даны плоскости П k и П l, такие, что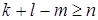 
, где m – размерность пересечения L m направляющих подпространств L k и L l, то П k и П l пересекаются.
Доказательство. Исключая тривиальный случай, когда какая-нибудь из данных плоскостей совпадает со всем пространством, имеет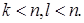 
В расположении двух данных плоскостей могут быть лишь три возможности:
либо П k параллельна П l;
либо плоскости П k и П l скрещиваются;
либо они пересекаются.
Если П k параллельна П l, то для размерности m пересечения соответствующих им пространств L k и L l имеем m = min (k, l). Теорема доказана.
2. Размерность многообразия k-плоскостей
Найдём размерность Р n,k, многообразия всех k-плоскостей
n- пространства.
Прежде всего заметим, что число параметров, от которых зависят k +1 точек M 0, M 1, …, M k n – пространства с линейно независимыми векторами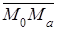 
, через которые проходит единственная k-плоскость, равно числу координат, 
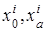этих точек, т. е. (k +1) n. Далее заметим, что число параметров, от которых зависят те же точки на k-плоскости, равно числу параметров 
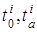этих точек, т. е. (k +1) k. Так как в n-пространстве, число параметров, от которых зависят точки 
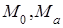равно сумме числа Р n,k и числа параметров, от которых зависят точки 
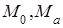на k-плоскости, то получим, что
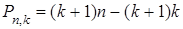, т. е.
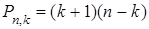. (6. 7)
§ 7. K -параллелепипеды в пространстве
1. Полуплоскости и параллелепипеды
Если в уравнении
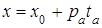(7. 1)
k-плоскости придавать одному из параметров t b только неотрицательные значения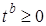 
, а остальным параметрам – произвольные действительные значения, мы получим k-полуплоскость, ограничиваемую (k-1)-плоскостью,
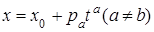(7. 2)
Если в том же уравнении (7. 1) придать всем параметрам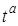 
только значения 
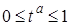, мы получим k-параллелепипед с вершинами
;
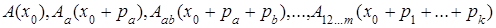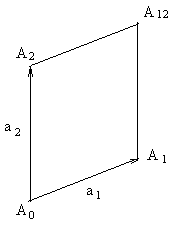
2-параллелепипеды называются параллелограммами.
Условимся называть k-параллелепипед с вершинами А 0, А 1, А 2, …, А 12…k параллелепипедом А 0 А 1 А 2 … А 12…k.
На рисунке 22 изображён 3-параллелепипед
А 0 А 1 А 2 А 3 А 12 А 13 А 123
и параллелограмм А 0 А 1 А 2 А 12.
а) 
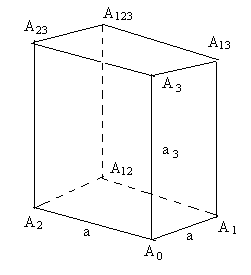б)
Рис. 22
2. Грани параллелепипеда
Придавая в уравнении (7. 1) значения 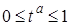всем параметрам 
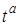при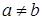 
, а параметру 
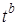- значения 
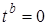или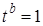 
, мы получим (k - 1)-параллелепипеды, являющиеся гранями k-параллелепипеда. Грани этих (k - 1)-параллелепипедов называются (k - 2)-гранями k-параллелепипеда, грани этих (k –3)-гранями k-параллелепипеда и т. д. Таким образом, k-параллелепипед обладает р – гранями, где р – пробегает значения от 0 до k – 1, 0-грани параллелепипеда совпадают с его вершинами, 1-грани называются рёбрами (при m = 2 - сторонами). На рисунке 22 (а) стороны параллелограмма – четыре отрезка А 0 А 1, А 0 А 2, А 0 А 3, А 0 А 12, А 1 А 13, А 2 А 12, А 2 А 23, А 3 А 13, А 12 А 123, А 13 А 123, А 23 А 123; 2-грани - шесть параллелограммов А 0 А 1 А 1 А 12, А 0 А 1 А 3 А 13, А 0 А 2 А 3 А 23, А 1 А 12 А 13 А 123, А 2 А 12 А 23 А 123, А 3 А 13 А 23 А 123.
Число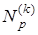 
р -граней k -параллелепипеда равно 
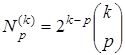, где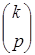 
- число сочетаний из k по р.
3. Объём прямоугольного параллелепипеда
Определим объём прямоугольного k-параллелепипеда, то есть такого k-параллелепипеда, у которого все векторы ра попарно перпендикулярны. Длина любого отрезка прямоугольного k – параллелепипеда называется его измерением.
Объём прямоугольного k-параллелепипеда называется его измерением.
Объём прямоугольного k-параллелепипеда только постоянным множителем отличается от произведения его измерений, т. е. функция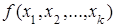 
отличается от произведения 
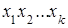измерений прямоугольного параллелепипеда только постоянным множителем 
.
В дальнейшем будем считать этот постоянный множитель равным 1, то есть будем считать, что объём V k прямоугольного k –параллелепипеда равен произведению его измерений.
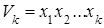(7. 4)
4. Объём произвольного параллелепипеда
Сравнивая прямоугольные k -параллелепипед и (k –1)-параллелепипед с объёмами, равному данному k -параллелепипеду и одной из его граней мы получим, что объём V k k-параллелепипеда равен произведению объёма V k-1 одной из его (k –1)-граней на расстояние h k между этой гранью и параллельной ей (k –1)-гранью.
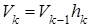(7. 5)
Если назвать выделенную (k –1)-грань k-параллелепипеда его основанием, а расстояние h k его высотой, то формула (7. 5) показывает, что объём k -параллелепипеда равен произведению объёма его основания на высоту.
Объём V k k -параллелепипеда, определяемого уравнением 
, при , определяется соотношением
,
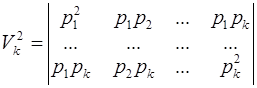т. е. квадрат объёма этого параллелепипеда равен определителю Грамма, составленному из k векторов ра.
Утверждение очевидно при k =1, когда параллелепипед совпадает с отрезком, определяемым вектором р 1, и объём этого параллелепипеда совпадает с длиной этого отрезка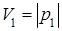 
, т. е. 
.
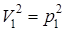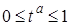Рассмотрим теперь k-параллелепипед и предположим, что наше утверждение справедливо для его (k – 1)-граней. Рассмотрим его (k – 1)-грань, определяемую уравнением , при и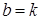 
. Тогда скалярный квадрат векторного произведения 
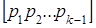в k-плоскости k-параллелепипеда, равный определителю Грамма, составленному из k–1 векторов 
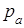(а < k), равен объёму этой (k – 1)-грани. Так как объём V k k-параллелепипеда равен произведению объёма V k-1 этой (k–1)-грани на соответствующую высоту h k, то объём V k равен
, (7. 7)
где j - угол между вектором р k и перпендикуляром к (k–1)-грани в k -плоскости k-параллелепипеда.
5. Аффинность k-параллелепипедов
Если даны два произвольных k-параллелепипеда А 0 А 1… А k… А 12…k и
В 0 В 1… В k… В 12…k, то системы точек А 0, А 1, …, А k и В 0, В 1, …, В k определяют аффинное преобразование, переводящее первые из этих точек во вторые. Так как при аффинном преобразовании плоскости переходят в плоскости, а параллельные плоскости в параллельные плоскости, это аффинное преобразование переводит весь k -параллелепипед А 0 А 1… А k… А 12…k в k -параллелепипед В 0 В 1… В k… В 12…k. Поэтому всякие два k -параллелепипеда аффинны.
Относительный объём k-параллелепипеда, определяемого уравнением и 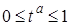, при аффинном преобразовании относительные величины преобразуются по формуле, то есть умножается на определитель матрицы этого аффинного преобразования, если k -параллелепипед с объёмом V k переходит при аффинном преобразовании с матрицей 
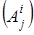в k-параллелепипед с объёмом 
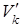, то
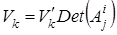(7. 8)
Отсюда вытекает, что отношения относительных объёмов k-параллелепипедов не изменяются при аффинных преобразованиях.
Выпуклые многогранники
В этом пункте будем рассматривать действительное k-мерное аффинное пространство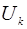 
, считая, что в нем дана аффинная система координат.
Пусть через некоторую точку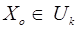 
имеющую координаты 
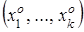, проведена прямая в направлении вектора 
, 
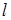координаты которого обозначим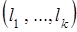 
. Согласно изложенному ранее эту прямую можно задать параметрическими уравнениями
, 
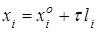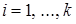. (7.9)
.
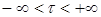Пусть на прямой (9) выбраны какие-нибудь точк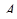и 
и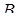 
. Соответствующие им значения параметра 
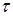обозначим 
и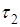 
. Предположим, что 
< .
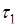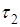Определение. Множество точек прямой, удовлетворяющих неравенством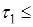 
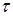
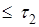, называется отрезок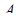 
.
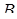Если точка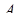 
имеет координаты 
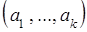, точка 
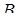имеет координаты 
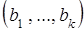, то в качестве направляющего вектора прямой можно взять вектор 
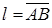. Тогда 
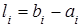, и для точки прямой имеем
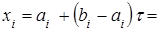
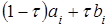, причем 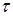= 0 в точке 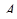, 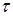= 1 в точке 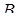, так что отрезок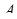 
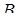задается теперь неравенствами 0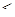 
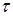
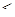1. Положим 1 
= 
, = 
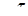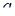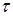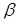. Тогда для точек отрезка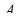 
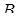и только для них имеем 
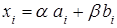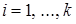, , (7.10)
, 
, 
.
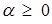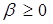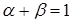Точка, в которой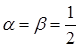 
, называется серединой отрезка .
Определение. Множество точек действительного аффинного пространства называется выпуклым, если вместе с каждыми двумя своими точками 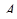, 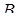оно содержит отрезок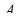 
.
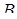Простейшими примерами выпуклых множеств могут служить: отрезок, плоскость любой размерности, все пространство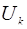 
.
Множество, состоящее из одной точки, и пустое множество также считается выпуклыми.
Из определения следует, что пересечение любой совокупности выпуклых множеств само является выпуклым множеством. В самом деле, если точки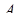 
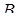, принадлежат пересечению некоторой совокупности выпуклых множеств, то отре
|
|
|
