 |
Аффинность k – симплексов.
|
|
|
|
Если даны два произвольных k – симплекса 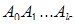 и
и 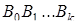 , то системы их вершин определяют аффинное преобразование, переводящее первую из этих систем вершин во вторую.
, то системы их вершин определяют аффинное преобразование, переводящее первую из этих систем вершин во вторую.
Так как при аффинном преобразовании плоскости переходят в плоскости, это аффинное преобразование переводит весь k – симплекс 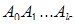 в k – симплекс
в k – симплекс 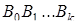 . Поэтому всякие два k – симплекса аффинны.
. Поэтому всякие два k – симплекса аффинны.
Относительный объем k – симплекса, определяемого уравнением (8.1) при 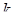 =
= 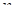 , где
, где  , выражается по формуле при аффинном преобразовании с оператором
, выражается по формуле при аффинном преобразовании с оператором 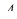 умножается на определитель матрицы оператора
умножается на определитель матрицы оператора  , получаем, что при аффинном преобразовании относительные объемы всех k – симплексов умножаются на определитель матрицы этого аффинного преобразования, т.е. если k – симплекс с относительным объемом
, получаем, что при аффинном преобразовании относительные объемы всех k – симплексов умножаются на определитель матрицы этого аффинного преобразования, т.е. если k – симплекс с относительным объемом 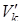 переходит при аффинном преобразовании с матрицей
переходит при аффинном преобразовании с матрицей 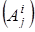 в k – симплекс с объемом
в k – симплекс с объемом 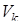 , то, так же как в случае k – параллелепипедов,
, то, так же как в случае k – параллелепипедов,
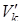 =
= 
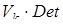
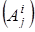 . (8.9)
. (8.9)
Отсюда вытекает, что отношения объемов k – симплексов не изменяются при аффинных преобразованиях.
Правильный k – симплекс
Определение правильных многоугольников и многогранников позволяет определить правильный k – симплекс.
Прежде всего построим правильный k – симплекс. Правильный k – симплекс при 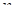 = 2 – равносторонний треугольник. Равносторонний треугольник
= 2 – равносторонний треугольник. Равносторонний треугольник 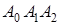 с центром в начале координат и со стороной
с центром в начале координат и со стороной 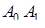 на прямой
на прямой 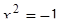 имеет вершины в точках с координатами
имеет вершины в точках с координатами 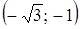 ,
,  и
и 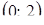 .
.

Рис. 29
Для построения правильного k – симплекса 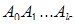 с центром в начале системы прямоугольных координат и с гранью
с центром в начале системы прямоугольных координат и с гранью 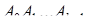 на плоскости
на плоскости 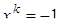 предположим, что мы построили аналитичный правильный
предположим, что мы построили аналитичный правильный 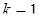 - симплекс.
- симплекс.
Так как центр О k – симплекса делит отрезок прямой 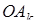 между точкой
между точкой 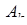 и плоскостью
и плоскостью 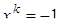 в отношении
в отношении 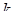 : 1, а прямая
: 1, а прямая 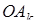 совпадает с
совпадает с 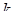 -ой координатной осью, вершина
-ой координатной осью, вершина 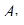 имеет координаты (0, 0, 0, …
имеет координаты (0, 0, 0, … 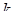 );
); 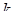 -е координаты вершин
-е координаты вершин 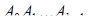 равны – 1, а первые
равны – 1, а первые 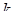 -1 координаты этих вершин можно получить из координат вершин (
-1 координаты этих вершин можно получить из координат вершин (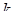 -1) - симплекса
-1) - симплекса 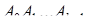 умножением их на такой множитель
умножением их на такой множитель 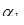 , чтобы все расстояния
, чтобы все расстояния 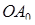 ,
, 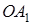 , …,
, …, 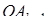 =
= 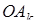 =
= 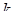
|
|
|
Расстояние от центра построенного 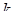 - симплекса
- симплекса 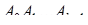 до его (
до его (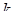 -1) – граней равно 1, а расстояние от того же центра до вершин этого
-1) – граней равно 1, а расстояние от того же центра до вершин этого 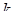 - симплекса равно
- симплекса равно 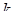 . Длина каждого из ребер этого
. Длина каждого из ребер этого 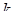 - симплекса равна
- симплекса равна 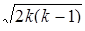 .
.
 Из определения правильного
Из определения правильного 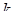 - симплекса видно, что все
- симплекса видно, что все 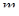 - грани правильного
- грани правильного 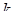 - симплекса являются правильными
- симплекса являются правильными 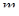 - симплексами.
- симплексами.
Рис.30
На рисунке изображен правильный (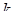 -1) – симплекс (
-1) – симплекс (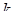 = 4)
= 4)
Объем правильного 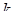 - симплекса.
- симплекса.
Вычислим объем построенного правильного симплекса. Так как объем основания этого 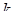 - симплекса равен произведению
- симплекса равен произведению 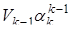 , а высота этого
, а высота этого  - симплекса равна
- симплекса равна 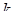 +1, получаем, что
+1, получаем, что
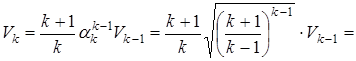
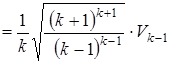 .
.
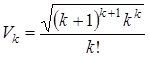 .
.
При 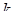 = 2 формула дает нам
= 2 формула дает нам 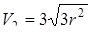 .
.
При  = 3 формула
= 3 формула 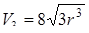 .
.
Объем правильного  - симплекса, (
- симплекса, ( -1) – грани которого находятся на расстоянии
-1) – грани которого находятся на расстоянии 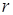 от его центра, равен
от его центра, равен
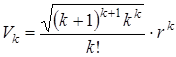 .
.
§ 9. K -шары в пространстве
Называть k -мерной сферой евклидова k -пространства или k-сферой этого пространства множество всех точек этого пространства, лежащих в одной (k + 1)-плоскости и отстоящих от данной точки, называемой центром k-сферы, на одном и том же расстоянии, называемом радиусом k-сферы.
При k = n – 1 k -сфера определяется как множество всех точек пространства, отстоящих от одной точки на одном и том же расстоянии: в дальнейшем, говоря «сфера», будем иметь в виду (n – 1)-сферу. При k = 1, k -сфера называется окружностью.
Если радиус (k – 1)-сферы равен R, то множество всех точек k -плоскости этой (k – 1)-cферы, находящихся от центра (k – 1)-cферы на расстоянии 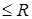 , называется k -шаром. При k = n n -шар определяется как множество всех точек n -пространства, отстоящих от центра сферы на расстоянии
, называется k -шаром. При k = n n -шар определяется как множество всех точек n -пространства, отстоящих от центра сферы на расстоянии 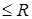 . В дальнейшем, говоря «шар», будем иметь в виду n -шар. При k = 2 k -шар называется кругом.
. В дальнейшем, говоря «шар», будем иметь в виду n -шар. При k = 2 k -шар называется кругом.
|
|
|
Если центр сферы – точка М 0(х 0), а радиус равен R (рис. 31), радиус-вектор х произвольной точки М сферы связан условием, состоящим в том, что расстояние М 0 М равно R. Так как это расстояние равно модулю вектора 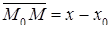 , т. е.
, т. е. 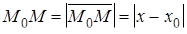 , то уравнение сферы с центром в точке М 0, и радиусом R имеет
, то уравнение сферы с центром в точке М 0, и радиусом R имеет
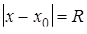 (9. 1)
(9. 1)
или, после возведения обеих частей уравнения (9. 1) в квадрат
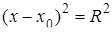 (9. 2)
(9. 2)
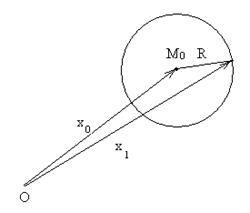
Рис. 31
Уравнению (9. 2) не удовлетворяет радиус-вектор ни одной точки, для которой расстояние М 0 М не равно R, так как и расстояние М 0 М и радиус R – положительные числа.
Уравнение (9. 2) называется векторным уравнением сферы. Это уравнением сферы. Это уравнение является частным случаем векторного уравнения поверхности. Поэтому сфера является частным случаем уравнения поверхности, так как k -сферу можно рассматривать как сферу в (k + 1)-пространстве.
Так как k -сфера с центром в точке М 0(х 0) и радиусом в некоторой (k + 1)-плоскости является пересечением сферы с тем же центром и радиусом с указанной (k + 1)-плоскостью, уравнениями k -сферы является уравнение (9. 2) сферы с тем же центром и радиусом и уравнения (k + 1)-плоскости.
Если центр сферы находится в начале, х 0=0, то уравнение (9. 2) примет вид
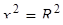 (9. 3)
(9. 3)
Уравнение (9. 2) можно переписать в виде
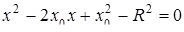 (9. 4)
(9. 4)
или, умножая обе части этого равенства на число а, в виде
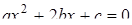 (9. 5)
(9. 5)
Вектор 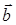 и число с в уравнении (9. 5) связаны с радис-вектором х 0 центра сферы и её радиусом R соотношениями
и число с в уравнении (9. 5) связаны с радис-вектором х 0 центра сферы и её радиусом R соотношениями
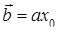 ,
, 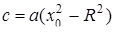 (9. 6)
(9. 6)
Поэтому, если дано уравнение (9. 5) сферы, то центр и радиус этой сферы определяются соотношениями.
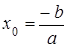 ,
, 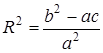 (9. 7)
(9. 7)
Уравнение (9. 5) при а = 1, т. е. уравнение
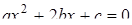 (9. 8)
(9. 8)
называется нормальным уравнением сферы. В случае нормального уравнения сферы соотношения (9. 7) показывает, что, для того чтобы уравнение (9. 5) было уравнением сферы, необходимо выполнение неравенства
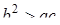 (9. 9)
(9. 9)
В случае, когда 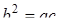 , уравнению (9. 5) удовлетворяет только одна точка М 0(х 0), которую можно рассматривать как сферу нулевого радиуса. Для того, чтобы общее уравнение второй степени было бы уравнением сферы, необходимо выполнение неравенства, равносильного неравенству (9. 9).
, уравнению (9. 5) удовлетворяет только одна точка М 0(х 0), которую можно рассматривать как сферу нулевого радиуса. Для того, чтобы общее уравнение второй степени было бы уравнением сферы, необходимо выполнение неравенства, равносильного неравенству (9. 9).
Геометрия k -сфер
1. Уравнение k -сфер
Определим k -сферы как пересечения сферы с (k +1)-плоскостью. Так как (k +1)-плоскость в свою очередь является пересечением n – k – 1 плоскостей, а каждая из этих плоскостей может быть заменена такой сферой, что указанная плоскость является радикальной плоскостью для этой сферы и данной сферы, k -сфера является пересечением n – k независимых сфер. Поэтому k – сферу можно задать n – k – уравнениями
|
|
|
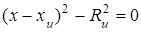
В этом случае произвольная сфера, проходящая через данную k -сферу, определяется уравнением
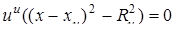 (9. 10)
(9. 10)
При k = n – 2 совокупность сфер с уравнениями вида (9. 10) составляет пучок сфер.
Если даны две сферы
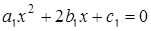 ,
,  ,
,
то совокупность сфер с уравнениями
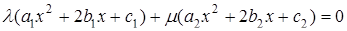 называется пучком сфер,
называется пучком сфер,
содержащем две сферы.
Уравнение при 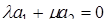 является уравнением плоскости.
является уравнением плоскости.
Взаимное расположение двух k -сфер
Две k -сферы k -пространства без общих точек будем называть зацепленными, если всякая сфера, проходящая через одну из этих k -сфер, пересекается со всякой сферой, проходящей через другую k -сферу. Будем называть две k -сферы k -пространства без общих точек незацепленными, если существуют непересекающиеся сферы, проходящие через эти k -сферы.
На рисунке изображены различные виды взаимного расположения двух окружностей в 3-пространстве.
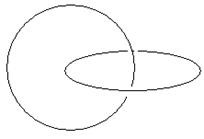

а) зацепление б) пересечение в точке
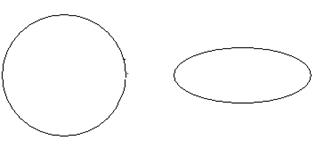
в) незацепление
Рис. 32
Объём сферы
Объём сферы радиуса r, который будем обозначать S k, выражается интегралом
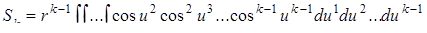 ,
,
в котором переменное 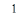 изменяется от 0 до 2 p, а переменные
изменяется от 0 до 2 p, а переменные 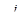 (при i > 1) от
(при i > 1) от 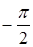 до
до 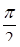 поэтому этот интеграл равен произведению k интегралов
поэтому этот интеграл равен произведению k интегралов
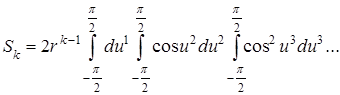

тогда объём S k сферы радиуса r в k -пространстве при чётном n равен:
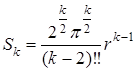 (9. 11)
(9. 11)
и для n чётного: 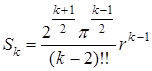
Формулы объёма дают при k = 2 (считая 0!! = 1), 3, 4 и 5 соответственно.
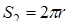 ,
, 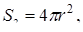
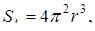
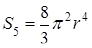 .
.
Объём шара
Объём шара радиуса r, который будем обозначать V k, выражается интегралом
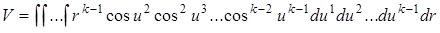
который с помощью интеграла (9. 11) для вычисления объёма сферы S k может быть записан в виде
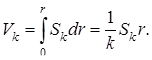
Поэтому объём V k шара радиуса r в k -пространстве при чётном и нечётном n соответственно равен
|
|
|
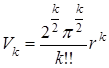 ,
, 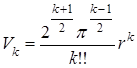 (9. 12)
(9. 12)
Формула (9. 12) дает при k = 2, 3, 4, 5 соответственно
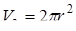 ,
, 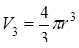 ,
,  ,
, 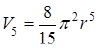 (9. 13)
(9. 13)
|
|
|


