Характерная или основная частота

Применим синусоидально модулированную фазу на обе противоположно распространяющиеся волны, тогда модулированная разность фаз

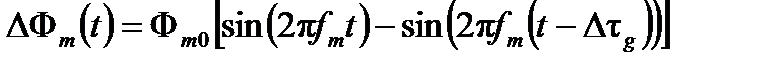(3.15)

 

или после применения тригонометрических преобразований

 

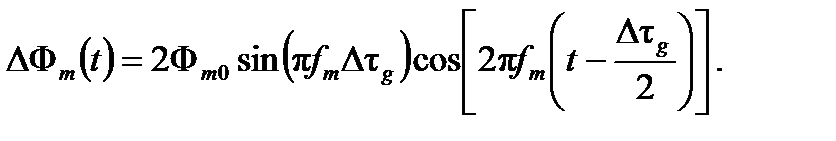(3.16)

 

Кольцевой интерферометр ведет себя как идеальный линейный фильтр задержки с синусоидальной передачей функции , так что имеется максимум (в абсолютном значении) так называемой характерной (или основной) частоты f_p (ранее определяемой как ) и ее нечетных гармоник и имеется обнуление в четных гармониках (Рисунок 3.9).

 

Выходной сигнал

Выходной сигнал

Модуляция смещения

Модулированный сигнал

1-я гармоника

Модуляция сдвига

Рисунок 3.8. Синусоидальная волна модуляции смещения: (а) в покое; (b) при вращении

(а)

(b)

Из этого результата следует, что выбор рабочей частоты не важен, но паразитные нелинейности или амплитудная модуляция в фазовой модуляции может снизить качество наклона [11]. Фактическое использование дополнительных модуляций для обнаружения максимума ответной кривой очень распространено, но точность в несколько десятых процента от ширины обычно достаточна. В волоконном гироскопе мы наблюдаем меньше, чем 10^–6, а потенциальные паразитарные эффекты необходимо оценить более тщательно.

Рисунок 3.9. Нормированная функция модуляции сдвига фаз

Точное отражение четных гармоник

L× fp≈ 100 м·МГц

Основные точки заслуживают того, чтобы быть повтореннными: поскольку сигнал интерференции функция автокорреляции, ответ совершенно симметричен относительно нуля, даже с асимметричным спектром (см. приложение 1).

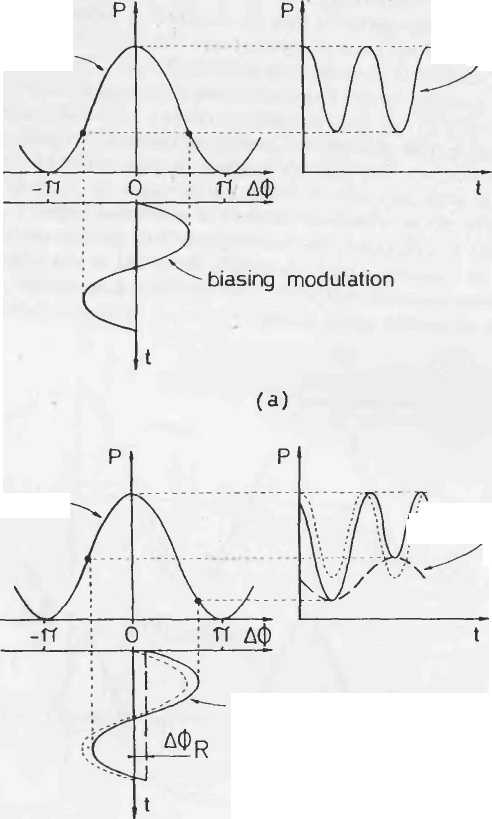
Уже в первом случае причиной ложного наклона является нелинейность модуляции фазы или электронного генератора. Модуляция чистого синуса (косинуса), центризованного относительно нуля дает только четные гармоники в модулированном ответе интерферометра, и частота демодулированного ответа на фундаментальные (и следовательно нечетные гармоники) является абсолютно нулевой. Однако если эти ложные четные гармоники благодаря нелинейным ответам цепи модуляции, добавочные компоненты частот нечетных гармоник, генерируемые в отклике, воспринимаются как ненулевые наклоны в демодуляции. Это легко можно увидеть в рисунке 3.10, который показывает, что вторичные гармоники дают несбалансированные модуляции, как и в случае со смещением вследствие вращения. В данном худшем случае вторичная гармоника должна давать менее 120 дБ (электрический) для того, чтобы ограничить наклон ниже 10^–6 рад! Этот эффект также зависит от соответствующей фазы основной фундаментальные частотной модуляции и паразитных четных гармоник.

Наклон смещения априори не наносит ущерб производительности гироскопа, если он устойчив, но на практике это восприимчиво к дрейфу, особенно с изменением условий окружающей среды. Как будет видно на протяжении всего этого анализа, лучшим способом для подавления дрейфа является подавление смещения! В случае нелинейного ответа модулятора простым решением является работа системы на собственной частоте [11] (или ее нечетных гармониках), и любые паразитные четные гармонические модуляции Ф _m (t) будут обнулены разностью фаз ΔФ _m (t), потому что, как мы видели, интерферометр ведет себя как линейный фильтр задержки. Обратите внимание, что поскольку эта модуляция распространяется на носителе очень высокой частоты, оптические волны не диспергируют для этих поднесущих компонент гармоник, которые распространятся с одной и той же групповой скоростью и пропускают совершенно периодические зазубрины.

 

(b) 0

смещение

2-я гармоника

Рисунок 3.10. Соответстующий дисбаланс модуляции: (a) с постоянным смещением; (б) с дополнительной модуляцией второй гармоники. (Сплошная кривая в каждом графике представляет собой сумму двух пунктирных кривых)

 

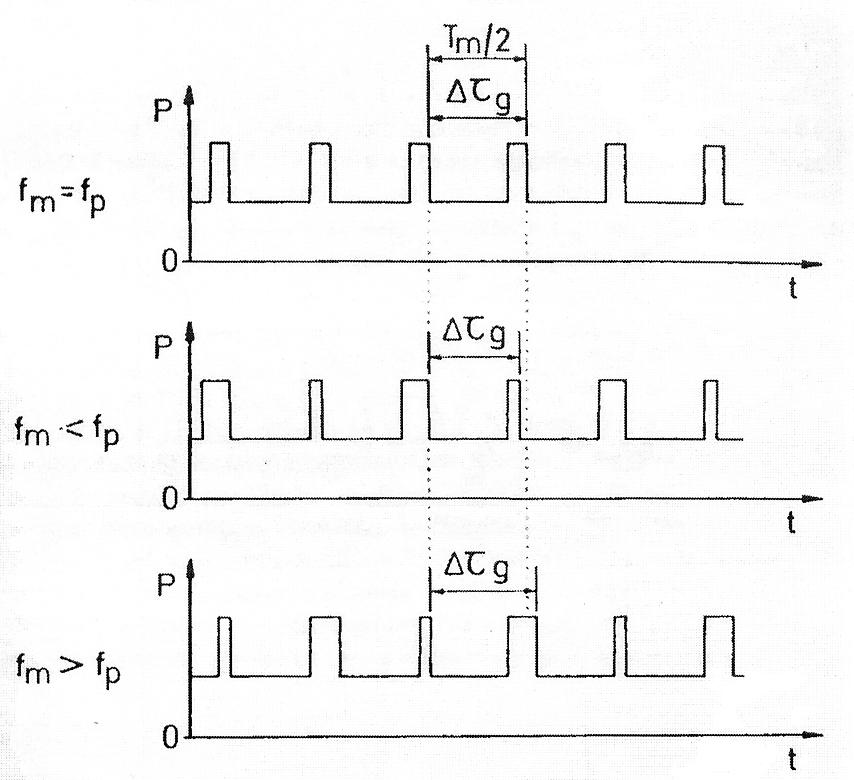
С квадратно модулированными волнами, нелинейные фазы модуляции отклика не являются вредными, так как Ф _m принимает только два значения, Ф _{m 1} и Ф _{m 2} и модуляции разности фаз ΔФ _m =±(Ф _{m 1}–Ф _{m 2}) всегда уравновешивалась около нуля. Если частота модуляции f_m не равна собственной частоте f_p, модуляции разности фаз принимает четыре значения (Рисунок 3.11):

 

 

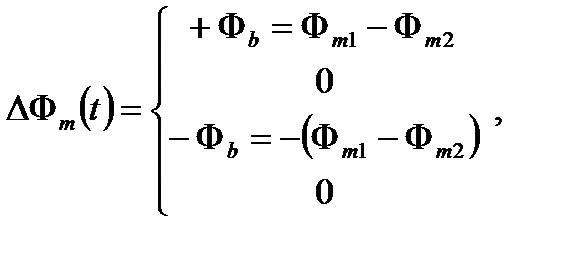(3.17)

 

но она по-прежнему является сбалансированной около нуля без каких-либо демодулирующих смещений наклона.

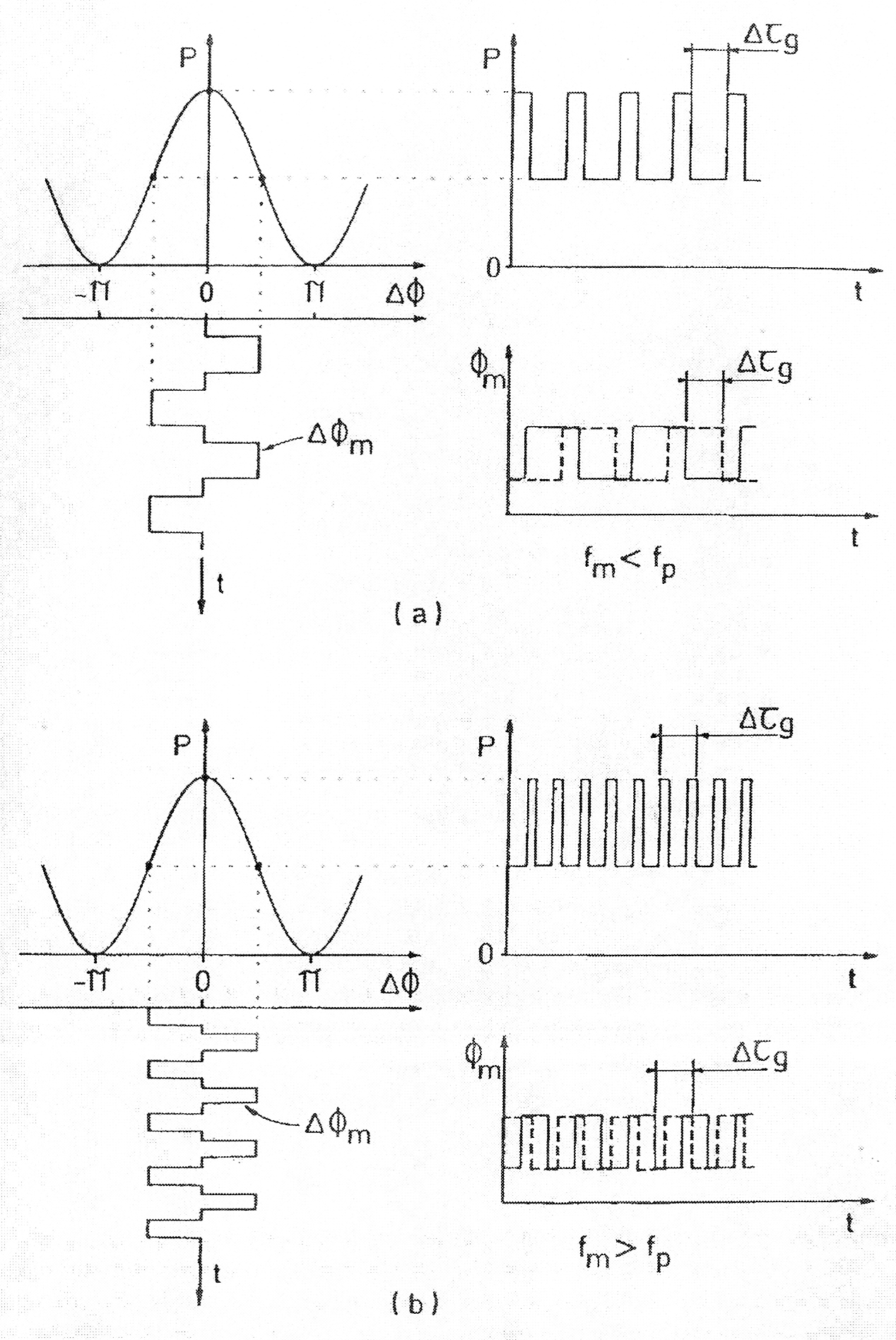
Рисунок 3.11. Форма волны модуляции с (a) fm<fp; (b) fm>fp

Тем не менее, могут возникнуть паразитные смещения с асимметрией циклического режима квадратно модулированных волн [12]:

 

(3.18)

 

где T_m – это период модуляции. С собственной частотой (где период T_m =2Δτ _g), разность фаз ΔФ _m (t) принимает четыре значения (Рисунок. 3.12):

 

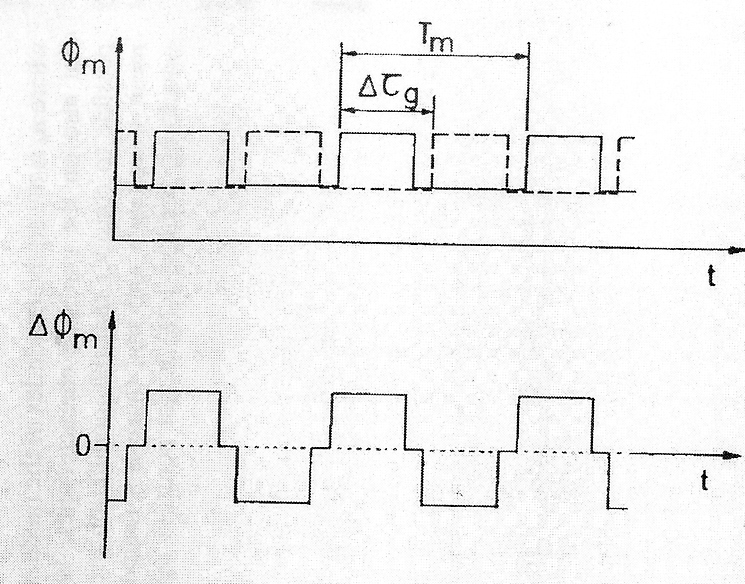
Рисунок 3.12. Модулируемая разность фаз с асимметричным циклическим режимом прямоугольных импульсов

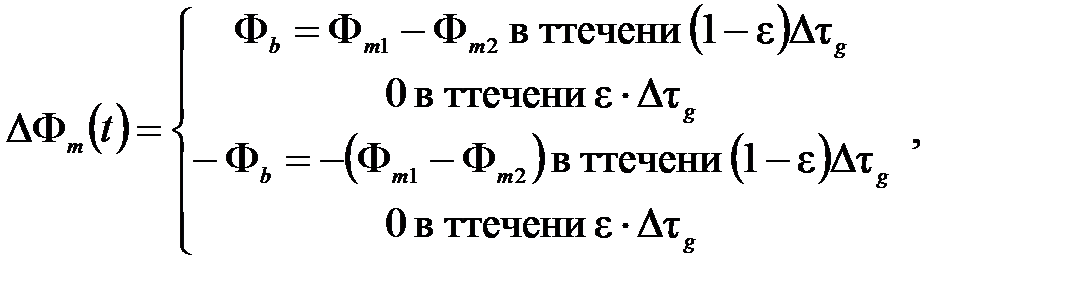(3.19)

 

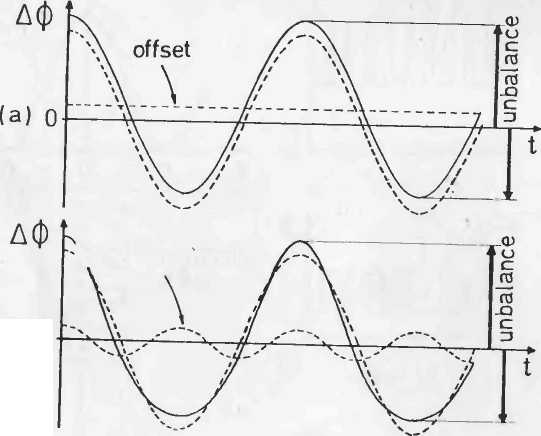
Когда гироскоп в покое, выходной сигнал состоит из лучей равной ширины , но когда частота модуляции f_m не равна f_p, один всплеск ширины уменьшается, в то время как другой – увеличивается (Рисунок 3.13).

Это дает очень сильный паразитный сигнал на модулированную частоту и, таким образом, ложное смещение демодулированного сигнала. Это очень чувствительной способ измерения собственной частоты [12]. Однако циклический режим с квадратными волнами нельзя сделать совершенно одинаковым 50-50 (особенно потому, что времена нарастания и сокращения в электронике обычно не равны), и это дает ложный наклон, от которого зависит частота модуляции и прохождение через ноль собственной частоты.

Поскольку собственная частота зависит от температуры (10^–5 /°C) в связи с тепловой зависимостью показателя преломления, время переноса делает это ложное смещение наклона не стабильным. Чтобы устранить этот недостаток, электронный вход должен использоваться для подавления лучей, которые носят ложный эффект в циклическом режиме 50-50.

Рисунок 3.13. Эффект асимметрической модуляции прямоугольных импульсов

Эта проблема делает использование квадратно модулированных волн более сложным, чем синусоидально модулированных, но, как будет видно далее, в замкнутом цикле цифровой обработки методы, использующие квадратные волны, являются настолько выгодными, что эта дополнительная сложность является разумным отпуском.

Последний паразитный эффект достигается благодаря остаточной интенсивности модуляции в фазовом модуляторе и может определяться как ложный сигнал основной частоты [11]. Эти модуляции также обратимы и наблюдаются одинаково для противонаправленных волн, но сигнал интерференции вытекает из разности фаз волны, тогда как интенсивности добавляются. Для интенсивности модуляции система также ведет себя как фильтр линии задержки, но в этом случае оно отвергает собственную частоту и ее нечетные гармоники. Для интенсивности модуляции перенос функции 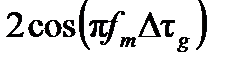; таким образом, операции с собственной частотой (или на нечетных гармониках) также устраняют эффект остаточной интенсивности модуляции. Обратите внимание, что это строго действительно только в покое, где разность фаз, вызванная ротацией, равна нулю. Во время вращения модуляции интенсивности может привести к некоторым паразитным эффектам, даже на f_p, которая изменяет коэффициент масштабирования [13].

Таким образом, использование действительно одномодового фильтра на общих портах ввода–вывода интерферометра превращает кольцевой волоконный интерферометр чувствительным только к таким необратимым эффектам, как эффект Саньяка. Кроме того, модуляция–демодуляция на основных или собственных частотах катушки (или на одной из ее нечетных гармониках) представляет сигнал смещения, который не ухудшает оригинальное совершенство системы. Эти два простых условия объединены в так называемой минимальной конфигурации [14], позволяющей несмотря на различные дефекты компонентов достигать высокого исполнения.

Примечание: Как обсуждается в приложении 1, модуляция фазы поддерживается на так называемой групповой скорости v_g как любой модуляции и не на фазовой скорости v

 

(3.20)

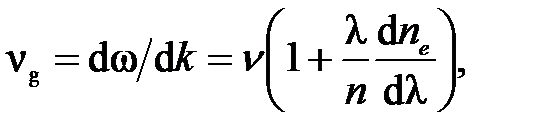
где n_e – эквивалентный показатель преломления моды, который зависит главным образом от материала, но и от характеристик системы управления. При использовании широкого спектра модуляция распространяется на групповую скорость со средней длиной волны. Существует временной разброс Δτ_s модуляции временной волны, потому что v_g (λ) не является постоянной в спектре шириной Δλ в котором производные второго порядка или 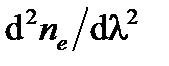, называемые распространением дисперсии, не равны нулю:

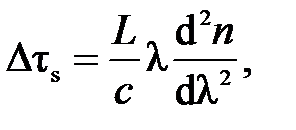(3.21)

 

Это значение часто приводится с 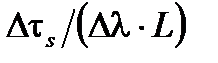в пс·нм^–1·км^–1. Ниже приводится дисперсия для кремнезема

 

λ (в нм)
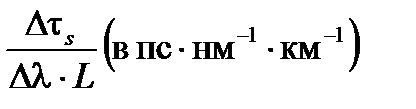
	–100	–30	≈0	+20

 

Этот эффект является очень важным в телекоммуникационных приложениях, где частота модуляции достигает гигагерцового диапазона с распространения вдоль волокон на километры; но он незначителен в случае волоконного гироскопа.

Период модуляции является предпочтительно двойным по сравнению с групповым временем транзита через катушку Δτ _g, а также с временным распространением Δτ _s также пропорциональным длине катушки, соотношение Δτ _s / Δτ _g не зависит от длины катушки. На 850 нм, где дисперсия имеет наибольшее значение, и с шириной спектра 50 нм, это соотношение составляет всего 0,1%. В случае возникновения квадратно модулированных волн это побуждает конечные рост и падение времени, но это не влияет на производительность волоконного гироскопа.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: