 |
Обратимые смещения модуляции-демодуляции
|
|
|
|
Взаимные конфигурации обеспечивают взаимное влияние сигнала в эффекте Саньяка с идеальным контрастом, после фаз, а также амплитуд обе противонаправленные волны совершенно равны в покое. Ответ оптической мощности затем является функцией косинуса 
индуцируемая вращением разность фаз, в которой 
является максимальной на нуле. Чтобы получить высокую чувствительность, этот сигнал должен быть смещен в точке эксплуатации с ненулевой ответной крутизной:
(3.4)
где Ф b – смещение фазы. Однако Ф b должно быть стабильным для ожидаемой чувствительности; то есть значительно лучше, чем 1 мкрад. Например, использование необратимого эффекта Фарадея (описано в разделе 7.1), регулируемого электрическим током, было предложено в [9], но это потребует регулировку отклонения тока с точностью лучше, чем 1 млн–1.
Проблема дрейфа отклонения фазы полностью преодолевается с помощью обратимого фазового модулятора, помещенного на одном конце катушки, и который выступает в качестве линии задержки (Рисунок 3.5) [10]. Из-за принципа обратимости обе интерферирующие волны несут точно ту же фазу модуляции 
, но сдвинутую во времени. Задержка равна разности 
группового времени переноса (см. приложение 1) между длинным и коротким путями, связывающими модулятор и разделитель. Это дает смещение модуляции 
как разность фаз
| Рисунок 3.5. Генерация смещенной фазы модуляции с использованием задержки через волоконную катушку |
| Волоконная катушка |
| Возвратно-поступательный фазовый модулятор |
|
(3.5)
и получаем сигнал интерференции
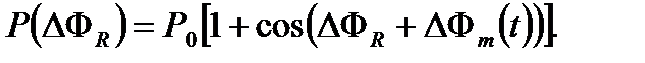(3.6)
Этот метод может быть реализован с прямоугольно-модулированной волной 
, где половина периода равна 
(это соответствует так называемой основной собственной частоте fpкатушки, 
и произведение длины катушки на собственную частоту составляет около 100 м·МГц для кримниевых волокон). Это дает смещение модуляции 
.В покое оба состояния модуляции дают одинаковые сигналы (Рисунок 3.6):
|
|
|
(3.7)
| Модуляция смещения |
| Рисунок 3.6. Отклонение прямоугольно модулированной волны |
| Покой Вращение |
| Выходной сигнал |
но в ротации
(3.8)
и разница между обоими состояниями становится
(3.9)
(3.10)
Этот сигнал «смещения» 
измеряется при демодуляции как сигнал детектора, усиливающегося для получения максимальной чувствительности до Ф b =π/2, при которой sinФ b =1.
| Рисунок 3.7. Размодулированный выходной сигнал и демодулированный сигнал смещения в волоконном кольцевом интерферометре |
| Стабильный нуль |
| Размодулированный выходной сигнал Сигнал смещения |
| ΔΦ |
Эта техника модуляции и демодуляции теперь широко воспринимается как техника оптимального смещения, поскольку она дает ответ синусом (производная ответа - косинус) с очень стабильным отклонением (Рисунок 3.7). Мощность, зависящая от Р 0 и смещение фазы, зависящее от sinФ b являются повторяющимися и следовательно не влияет на стабильность отклонения. Использование обратимого фазового модулятора является основополагающим, поскольку он дает модуляцию разности фаз, центрируемую около нуля. На самом деле, для любой прямоугольно модулированной волны
модуляция разности фаз всегда 
Это техника обратимого смещения может осуществляться в качестве альтернативы с модуляцией по косинусу 
[4,10], которая дает ответ, не требующий фазовой модуляции с плоским откликом по частоте. Обнаруженный сигнал может быть разложен на гармонические составляющие модуляции частоты fm
(3.11)
(3.12)
Используя Jn разложение Бесселевой функции, получим
|
|
|
(3.13)
Четные гармоники по-прежнему пропорциональны 
с ненаклонным откликом, но нечетные гармоники и особенно основной частоты пропорциональны sinФ R. С синхронизацией демодуляции это дает отклоняющийся сигнал:
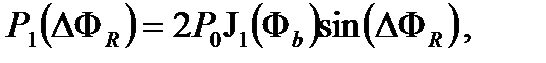(3.14)
Максимальная чувствительность теперь получается для Ф b ≈1,8 рад (вместо π/2≈1,5 с прямоугольной волной) и J 1(1.8) = 0.53. В состоянии покоя сигнал детектора состоит главным образом из компонент вторичных гармоник, но в ротации представляется несбалансированная модуляция, содержащая сигнал на основной частоте (Рисунок 3.8). (Обратите внимание, что мы называем первой гармоникой основную частоту и второй гармоникой – двойную основную частоту).
|
|
|
