 |
Шум, дрейф и масштабный фактор
|
|
|
|
В покое выходной сигнал волоконного гироскопа является случайной функцией, которая складывается из белого шума (с теоретического предела фотонов, которые образуют шум) и медленно варьируется той или иной функцией с учетом долгосрочного дрейфа среднего значения. Белый шум выражается в терминах стандартного отклонения курса как эквивалент вращения и оценивается корнем квадратным от пропускной способности (т.е. градусов в час корень квадратный из герц или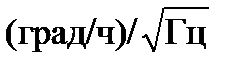 
). Эквивалент спектральной плотности мощности шума может использоваться вместо площади стандартного отклонения (т.е. (град/ч)2/Гц). Третье возможное определение является так называемым случайным блужданием в 
, которое имеет одно измерение как стандартное отклонение, но 
равен 1/60 . Случайное блуждание дает больше «отпечатков» номеров, но это только особая единица для оценки белого шума.
В частности случайное блуждание не следует путать с дрейфом, границы которого оценивают от пика до пика долгосрочных вариантов средних значений выходного сигнала (Рисунок 2.14). Дрейф обычно выражается в ±град в час. В волоконных гироскопах ограничение шума составляет обнаружение шума, которое зависит главным образом от суммы возврата оптической мощности; но дрейф, который может теоретически отсутствовать, соответствует отсутсвию недостатка "обратимости", который мы будем анализировать.
Шум и дрейф предъявляют различные требования, которые зависят от приложений. Низкий уровень шума имеет большое значение для стабилизации отклика и управления, но для навигации дрейф является более фундаментальным параметром. Сигнал скорости вращения интегрирован для получения изменения в угловой ориентации, и этот процесс интегрирования производит усреднение белого шума, которое представляет эффект стремления к долгосрочному преобладанию.
|
|
|
Другой очень важной характеристикой гироскопа является коэффициент масштабирования. Фактически по сравнению с другими датчиками гироскоп нуждается в гораздо лучшей точности в более широком динамическом диапазоне: важным измерением является общий угол поворота, и прошлые ошибки понижают будущую информацию. Очень важно иметь низкий уровень шума и дрейфа для измерения очень низких значений, но также важно иметь и точное измерение высоких значений (т.е. точность масштабного фактора). Требуемое исполнение зависит от вида траектории, и они точно определяют сложность системы анализа и моделирования, но большинство приложений обычно подразделяются на три вида:
| сигнал оценки вращения |
| Рисунок 2.14. Пример систематической погрешности с шумом и долгосрочным дрейфом |
| время |
| дрейф |
| шум |
| Смещения белый шум или случайные блуждания | Направление наклона (значение) | Масштабный фактор точности (значение σ) | |
| Инерциальный класс Тактический класс Нормальный класс | <0.00l град/√час 0.5до 0.05 град/√час >0.5 град/√Гц | <0.0l град/час 0.1до 10 град/час 10 до 1000 град/час | <5 млн–1 10 до 1000 млн–1 0.1 % до 1 % |
Как будет видно, технология волоконного гироскопа особенно подходит для тактического класса приложений. Инерциальный класс применения возможен, но здесь будет труднее конкурировать с лазерным гироскопом, который достиг очень сильных позиций в этом сегменте рынка.
Пропускная способность
Минимальное время отклика интерферометрического волоконного гироскопа это время транзита через катушку волокна (т.е. 1 мс с длиной около 200 м). Это дает очень высокую теоретическую пропускную способность в несколько сотен килогерц. Как будет видно далее, методы обработки сигнала, которые обязательно должны использоваться, снижают пропускную способность, но на практике достигаются диапазоны частот в несколько килогерц, что является весьма существенным улучшением по сравнению с предыдущими технологиями.
|
|
|
Важно отметить, что уровень сигнала это усредненное транзитное время. Таким образом, сигнал выборки с этой периодичностью не дает какой-либо потери информации для общего угла вращения [16], и последующие в усреднения дают точное среднее значение. Некоторые предлагаемые методы обработки сигнала используют ограничение сигнала и отбора проб с длительной периодичностью (см. раздел 10.2), и это важно осознавать, так как может привести к ошибке, если в полосе частот сигнала скорость слишком высока, поскольку колебания значений в процессе пропускания не принимаются во внимание.
Как отмечено в работе [17], интерферометрический волоконный гироскоп обычно рассматривается как нормальный гироскоп; то есть основные измерения является сигналом скорости вращения. Тем не менее, принимается во внимание только избыточное время транзита через катушку волокна, значения усреднены, и волоконный гироскоп может рассматриваться в этом случае, как нормальный интегрирующий гироскоп; то есть основные измерения угла поворота, следовательно, математически, является средним эквивалентным для интеграции.
Ссылки
[1] Саньяк Г., г., "L'ether lumineux demontre номинальная I'effel du жерл relatif d'ether dans ООН inlerferomelre en вращения unifornie," Conipie-rendus де I'Academie des наук, том 95, 1913, pp. 708-710. Sagnac, (i., "Грех Привет preuve de la rcalite тик 1 эфир luinineux номинальная I'experience dc lintcrfcrogiaplie louriiaiit," конт rendus де I'Acailemie наук, том 95, 1913, pp. 1410 — 1413.
[2] Пост Е. Ж. Эффект Саньяка, Обзор современной физики, том 39, 1967 г., стр. 475-494.
[3] Ардити Г.Ж. и Г. C. Лефевр, "Эффект Саньяка в волоконных гироскопах," Оптика письма, том 6, 1981, pp. 401-403 (SPIE MS 8, стр. 105-107).
[4] Лееб В.Р., Г. Шиффнер и Е. Шейтерер, "Оптоволоконные гироскопы: эффекты Саньяка и Физо," Приложения оптики, Vol. 18, 1979, pp. 1293-1295 (SPIE MS 8. pp. 85-87).
[5] Пост, Е.Ж., "Интерферометрическая разность хода, обусловленная движением," J.O.S.A., Vol. 62, 1972, стр. 234-239 (SPIE MS 8, pp. 79-84).
[6] Ардити Г.Ж. и Г. C. Лефевр, "Теоретические основы эффекта Саньяка в оптоволоконных вращающихся сенсорах, серия новостей в оптических науках, Vol. 32, 1982 г., стр. 44-51.
|
|
|
[7] Розенталь А.Г. "Регенерация циркуляции нескольких интерферометрирующих лучей для изучения воздействию распространения света," J.O.S.A., том 52, 1962, pp. 1143-1148.
[8] Štepánek, в. м. и д. Т. М. Дэвис, "Скорость вращения зондирования с прохождением волны в кольцевом лазере," Прикладная физика письма, Vol. 2, 1963, pp. 67-68.
[9] Иезекииль, S. и г. е. Кнаузенбергер, и др., "Инерциальные лазерные датчики вращения, '" SPIE материалы. Vol. 157, 1978.
[10] Чоу, в. в., д. Геа-Баналохе, л. м. Пердролти, в. е. Сандерс, в. Шлейх и м. о. Скалли, "Кольцевой лазерный гироскоп". Обзор современной физики, том 57, 1985, стр. 61.
[11] Иезекииль, С. и С. Р. Бальзамо. "Пассивный кольцевой резонатор лазерного гироскопа," Прикладная физика, письма, том 30, 1977, pp. 478-480 (SPIE MS 8, pp. 457-459).
[12] Мейер, е. р., S. Иезекииль, Стов д. в. и. я. Текип, "Пассивный волоконно-оптический кольцевой резонатор для измерения вращения," письма оптики, том 8, 1983, pp. 644-646 (MS SPIE 8, pp. 467-469).
[13] Пирхер г. и. г. Гепнер, "Совершенствование расположения интерферометрического лазерного гироскопа," французский патентной 1.563.720, 1967.
[14] Вали,. и р. в. Shorthill, "Кольцевой волоконный интерферометр", прикладной оптики. Vol. 15, 1976, pp. 1099-1100 (MS SPIE 8, стр. 135-136).
[15] Лефевр, х. C, S. Ватоукс, м. Папухон и C. Пуеч, "Комплексные оптики: практическое решение для волоконно-оптического гироскопа," SPIE труды, том 719, 1986, pp. 101 — 112 (SPIE MS 8, стр. 562-573).
[16] Лефевр, х. C, ф. Грайндорг, х. ж. Ардити, с. Ватоукс и м. Папухон, "Двойной закрытый петлеобразный гибридный волоконный гироскоп, использующий цифровой наклон фазы", труды ФУСШ ЗЛ85, OSA/IEEE, Сан-Диего, posldeadline документ 7, 1985 (SPIE MS8, pp. 444-447).
[17] Фидрик, В., д. Тазартес, а. Кордоба и Марк Дж., "Нормальный интегрирующий волоконно-оптический гироскоп: от теоретической концепции до системной механизации," SPIE труды, том 1585, 1991, pp. 437-448.
|
|
|
