 |
Уравнения, допускающие понижения порядка.
|
|
|
|
Уравнения порядка выше первого: случай понижения порядка.
Общие понятия.
ДУ порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде: F(x;y;y';y'')=0 (1) или, если это возможно, в виде, разрешенном относительно старшей производной: y''=f(x;y;y'). (2)
Решением ДУ (2) называется всякая функция y=p(x), которая при подстановке в уравнение обращает его в тождество.
Общим решением ДУ (2) называется функция y=p(x;c1;c2), где c1 и c2 - не зависящие от x произвольные постоянные, удовлетворяющие условиям:
1) p(x;c1;c2) является решением ДУ для каждого фиксированного значения c1 и c2.
2) Каковы бы не были начальные условия y(x0)=y0, y'(x0)=y'0 (3), существуют единственные значения постоянных c1=C1 и c2=C2 такие, что функция y=p(x;C1;C2) является решением уравнения (2) и удовлетворяет начальным условиям (3).
Всякое решение y=p(x;C1;C2) уравнения (2) получающееся из общего решения y=p(x;c1;c2) при конкретных значениях c1=C1; c2=C2 называется частным решением.
Решения ДУ (2), записанные в виде P(x;y;c1;c2)=0, P(x;y;C1;C2)=0, называются общим и частным интегралом соответственно.
График всякого решения ДУ второго порядка называется интегральной кривой. Общее решение ДУ (2) представляет собой множество интегральных кривых, а частное решение - одну интегральную кривую этого множества, проходящую через точку (x0;y0) и имеющая в ней касательную с заданным угловым коэффициентом y'(x0)=y'.
Уравнения, допускающие понижения порядка.
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим 3 типа уравнений:
|
|
|
I. Пусть дано уравнение y''=f(x) (4). Порядок можно понизить, введя новую функцию p(x), положив y' = p(x). Тогда y''=p'(x) и получаем ДУ первого порядка: p'=f(x). Решив его, т.е. найдя функцию p=p(x), решим уравнение y'=p(x). Получим общее решение заданного уравнения (4).
Но на практике поступают иначе: порядок понижается непосредственным интегрированием уравнения.
Так как y''= (y')'= 
, уравнение (4) можно записать в виде 
Тогда, интегрируя уравнение y''=f(x), получаем: y'= 
, или y'=p1(x)+c1. Далее, интегрируя полученное уравнение по х, находим: 
- общее решение данного уравнения.
Если дано уравнение 
то проинтегрировав его последовательно n раз, найдем общее решение уравнения: 
.
II. Пусть дано уравнение y''=f(x;y') (5) не содержащее явно искомой функции y. Обозначим y'=p, где p=p(x) - новая неизвестная функция. Тогда y''=p' и уравнение (5) принимает вид p'=f(x;p). Пусть p=g(x;c1) - общее решение полученного ДУ первого порядка. Заменяя функцию p на y', получаем ДУ: y'=g(x;c1). Оно имеет вид (4). Для отыскания y достаточно проинтегрировать последнее уравнение. Общее решение уравнения (5) будет иметь вид y= 
.
Частным случаем уравнения (5) является уравнение y''=f(y') (6) не содержащее также и независимую переменную x. Оно интегрируется тем же способом y'=p(x), y''= 
. Получаем уравнение p'=f(p) c разделяющимися переменными.
Если задано уравнение вида F(x;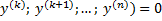 
(7), которое также не содержит явно искомой функции, то его порядок можно понизить на k единиц, положив 
=p(x). Тогда 
и уравнение (7) примет вид F(x;p;p';...; 
)=0.
III. Рассмотрим уравнение y''=f(y;y') (8), которое не содержит явно независимой переменной x.
Для понижения порядка уравнения введем новую функцию p=p(y), зависящую от переменной y, полагая y'=p. Дифференцируем это равенство по x, учитывая, что p=p(y(x)): 
, т.е. y''=p'*p. Теперь уравнение (8) запишется в виде p*p'=f(y;p). Пусть p=g(y;c1) является общим решением этого ДУ первого порядка. Заменяя функцию p(y) на y', получаем y'=g(y;c1) - ДУ с разделяющимися переменными.
|
|
|
Интегрируя его, находим общий интеграл уравнения (8): 
.
Частный случай уравнения (8) y''=f(y) решается аналогично.
|
|
|
