 |
ЛОДУ второго порядка с постоянными коэффициентами. Случай комплексных корней характер-го уравнения. Линейная независимость решений.
|
|
|
|
ЛОДУ второго порядка:
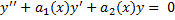(1)
Его характ-е уравнение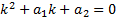 
, в зависимости от значения дискриминанта 
,
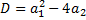может иметь комплексные корни. В этом случа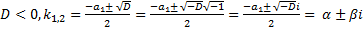е 
, где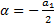 
, 
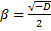. Мы должны доказать, что функции 
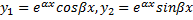удовлетворяют уравнению. Находим 
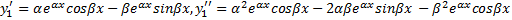, подставляем в уравнение: 
. Рассмотрим по отдельности коэффициенты п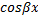ри 
и при 
: 
, 
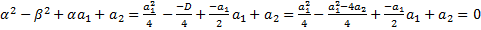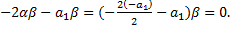Итак,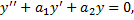 
т.е. функция 
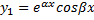- действительно решение уравнения. Аналогично доказывается, что и функция 
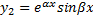- решение уравнения. Вронскиан этой системы функций: 
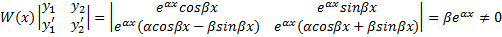, т.е. это - ФСР. И полученные решения линейно независимы. Общее решение уравнения (1) в данном случае: 
.
Структура общего решения однородного линейного дифференциального уравнения с постоянными коэффициентами порядка выше первого. Неоднородное уравнение со специальной правой частью.
Задача нахождения общего решения ЛОДУ n-го порядка (n>2) с постоянными коэффициентами
, (1)
где pi, i=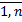 
- числа, решается аналогично случаю уравнения второго порядка с постоянными коэффициентами.
Сформулируем необходимые утверждения. Частные решения уравнения (1) также ищем в виде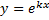 
, где k- постоянное число.
Характеристическое уравнение для уравнения (1) имеет вид:
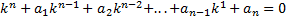(2)
Уравнение (2) имеет, как известно, n корней (в их числе могут быть и комплексные). Обозначим их через 
.
I случай:
Все корни уравнения (2) действительны и просты. Тогда функции 
являются частными решениями уравнения (1) и образуют ФСР. Поэтому общее решение уравнения (1) записывается в виде:
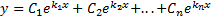
II случай:
Все корни характерестического уравнения действительные, но не все простые (есть корни, имеющие кратность m>1). Каждому простому корню k соответствует одно частное решения вида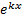 
, а каждому корню k кратности m>1 соответствует m частных решений: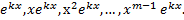 
И общее решение записывается как сумма частных решений уравнения.
|
|
|
III случай:
если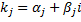 
- простой комплексный корень характеристического уравнения (здесь 
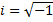- мнимая единица), то корнем характеристического уравнения будет и сопряженное с kj число
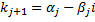. Паре корней 
соответствуют функции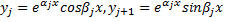 
в ФСР;
если 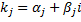- комплексный корень характеристического уравнения кратности r > 1, то корнем характеристического уравнения той же кратности будет и число 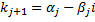. Паре корней , каждый из которых имеет кратность r > 1, соответствуют набор функций 
в ФСР.
ЛНДУ со специальной правой частью.
Для простоты рассмотрим ЛНДУ второго порядка. (для порядков выше 2 рассуждения аналогичны).
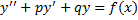,где p,q- некоторые числа (1)
Согласно теореме об общем решении ЛНДУ, общее решение (1) представляет собой сумму общего решения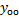 
соответствующего однородного уравнения и частного решения 
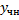неоднородного уравнения.
Для уравнения с постоянными коэффициентами (1) существует простой способ нахождения 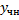, если правая часть f(x) уравнения (1) имеет так называемый "специальный вид":
I.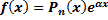 
или
II.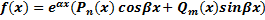 
Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f(x) уравнения (1) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют её в уравнение (1) и из полученного тождества находят значения коэффициентов.
Случай.
Правая часть имеет вид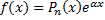 
, где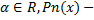 
многочлен степени n. Уравнение (1) будет иметь вид: 
. (2)
В этом случае частное решение 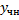ищем в виде:
, (3)
где r - число, равное кратности α как корня характеристического уравнения 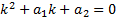(т.е. r-число, показывающее, сколько раз α является корнем характер-го уравнения.), а 
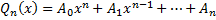- многочлен степени n, записанный с неопределенными коэффициентами 
.
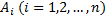а) Пусть α не является корнем характер-го уравнения, т.е. α≠k1,k2. Следовательно,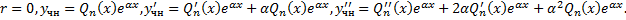 
После подстановки функции 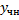и её производных в уравнение (2) и сокращения на 
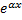, получим:
|
|
|
(4)
Слева - многочлен степени n с неопределенными коэффициентами, справа - многочлен степени n, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях x, получим систему (n+1) алгебраических уравнений для определения 
.
б) Пусть α является двукратным корнем характеристического уравнения, т.е α=k1=k2. В этом случае 
, поэтому уравнение (4) принимает вид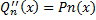 
Слева стоит многочлен степени n-2. Понятно, чтобы иметь слева многочлен степени n, частное решение 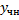следует искать в виде 
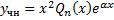(в равенстве (3) принять r=2).
в) Пусть α является однократным (простым) корнем характеристического уравнения, т.е. α=k1≠k2.
В этом случае искать решение в форме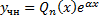 
нельзя, т.к. 
и уравнение (4) принимает вид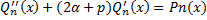 
.
В левой части - многочлен степени (n-1), в правой части - степени n. Чтобы получить тождество многочленов частное решение 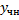следует искать в виде 
(в равенстве (3) положить r=1).
Случай.
Правая часть имеет вид 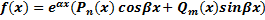, где Pn(x) и Qm(x) - многочлены степени n и m соответственно, α и β - действительные числа. Уравнение (1) запишется в виде
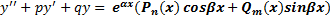(5)
Можно показать, что и в этом случае частное решение 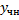уравнения (5) следует искать в виде
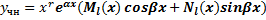(6)
где r - число равное кратности α ± βi как корня характер-го уравнения, Ml(x) и Nl(x) -многочлены степени l с неопределенными коэффициентами, l - наивысшая степень многочленов Pn(x) и Qm(x), т.е. l=max(n,m).
Замечания.
1. После подстановки функции (6) в (5) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.
2. Форма (6) сохраняется и в случаях, когда Pn(x)=0 или Qm(x)=0.
3. Если правая часть уравнения есть сумма функций вида I и II, то для нахождения 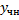следует использовать теорему о наложении решений:
Если правая часть уравнения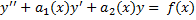 
представляет собой сумму двух функций: f(x) =f1(x)+f2(x), а 
и 
- частные решения уравнени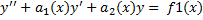й 
и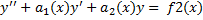 
соответственно, то функция 
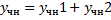является частным решением уравнения .
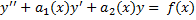Системы дифференциальных уравнений. Нормальная форма записи. Задача Коши и формулировка теоремы существования и единственности её решения в случаях: а) одного уравнения первого порядка; б)одного уравнения порядка выше первого; в) системы уравнений первого порядка в нормальной форме.
|
|
|
Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.
Общий вид систем ДУ первого порядка, содержащий n искомых функций y1,y2,...,yn, следующий:
Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида
(1)
называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.
Решением системы (1) называется совокупность из n функций y1,y2,...,yn, удовлетворяющих каждому из уравнений этой системы.
Начальные условия для системы (1) имеют вид:
y1(x0)=y10, y2(x0)=y20,...yn(x0)=yn0 (2)
Задача Коши и формулировка теоремы существования и единственности её решения в случаях:
|
|
|
