 |
A) Задача Коши (задача с начальным условием).
|
|
|
|
Пусть функция f(x, y) определена в области D, точка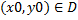 
. Требуется найти решение уравнения 
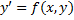; (3)
удовлетворяющее начальному условию y(x0) = y0; (4)
(начальное условие (4) часто записывают в форме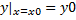 
).
Теорема Коши (существования и решения задачи Коши).
Если в области D функция f(x, y) непрерывна и имеет непрерывную частную производную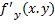 
, то для любой точки 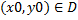в окрестности точки x0 существует единственное решение задачи ((3),(4)).
Эта теорема приводится здесь без доказательства. На самом деле для существования решения в окрестности точки x0 достаточно только непрерывности функции f(x, y); условие непрерывности 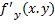обеспечивает единственность этого решения.
б) Постановка задачи Коши для уравнения n-го порядка:
требуется найти решение уравнения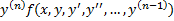 
; (5)
удовлетворяющее начальным условиям
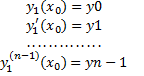(6)
где y0, y1, y2, …, yn-1 - заданные числа.
В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x0, y0,) с заданным угловым коэффициентом y1.
Теорема существования и единственности решения задачи Коши:
Пусть функция f(x, y, p1, p2, …, pn-1) непрерывна и имеет непрерывные частные производные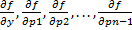 
в некоторой области D n + 1-мерного евклидового пространства переменных (x, y, p1, p2, …, pn-1), и пусть точка (x0, y0, y1, y2, …, yn-1) принадлежит области D. Тогда в некоторой окрестности точки x0 существует решение уравнения (5), удовлетворяющее начальным условиям (6). Это решение единственно.
в) Задача Коши для системы (1) ставится следующим образом: найти решение системы (1), удовлетворяющее начальным условиям (2).
Теорема существования и единственности решения задачи Коши.
Если в системе (1) все функции fi(x;y1;...;yn) непрерывны вместе со всеми своими частными производными по yi в некоторой области D ((n+1)-мерного пространства), то в каждой точке Mo(x0;y10;y20;...;yn0) этой области существует, и при том единственное, решение y1=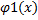 
, y2=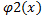 
,..., yn= 
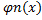системы, удовлетворяющее начальным условиям (2).
|
|
|
Редукция нормальной системы ДУ к одному уравнению высшего порядка.
Одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. Техника этого метода основана на следующих соображениях.
Пусть задана нормальная система
(1).
Продифференцируем по x любое, например первое, уравнение:
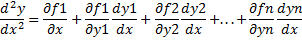
Подставив в это равенство значения производны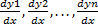 
х из системы (1) получим
,
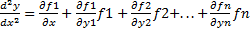или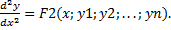 
Продифференцировав полученное равенство ещё раз и заменив значения производных 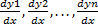из системы (1), получим
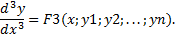
Продолжая этот процесс (дифференцируем - подставляем - получаем), находим
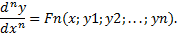
Соберем полученные уравнения в систему:
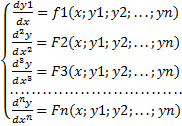(2)
Получили нормальную систему из n ДУ.
Редукция одного уравнения высшего порядка к нормальной системе уравнений первого порядка.
Рассмотрим редукцию на примере ДУ третьего порядка:
y'''=f(x;y;y';y'')
Производим замену y'=p, y''=p'=q и сводим ДУ третьего порядка к нормальной системе ДУ:
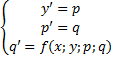
Матричная форма записи нормальной системы линейных ДУ первого порядка. Вывод характеристического уравнения для однородной системы с постоянными коэффициентами.
Обычная система ДУ имеет вид
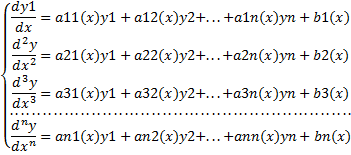
где aij(x) и bj(x) - известные, а yj(x) - неизвестные функции, (i=1,2,...,n. j=1,2,...,n) называется линейной системой ДУ.
При описании линейных систем дифференциальных уравнений удобнее пользоваться векторной(матричной) формой записи. Обозначим:
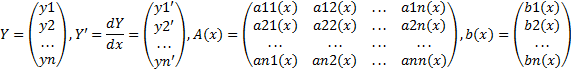
Тогда линейная система ДУ в матричной форме записывается в виде Y'=A(x)Y+b(x) или, что то же самое, в виде
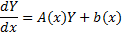
Матрица А называется матрицей системы, а вектор -функция b(x) - неоднородностью системы.
Система Y'=A(x)Y+b(x) называется неоднородной линейной системой ДУ, а система Y'=A(x)Y - однородной линейной системой.
|
|
|
|
|
|
