 |
Определитель Вронского и его свойства.
|
|
|
|
Рассмотрим ЛОУ. 
- какие-то решения ЛОУ.
Определителем Вронского (вронскиан) называется W(x)= 
Теорема о вронскиане линейно зависимой системы функций. Если система функций y1(x), y2(x), …, yn(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.
Док-во. Если функции y1(x), y2(x), …, yn(x) линейно зависимы на интервале (a, b), то найдутся числа c1,c2,...,cn, из которых хотя бы одно отлично от нуля, такие что
для 
.
Продифференцируем по x равенство n - 1 раз и составим систему уравнений:
Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно c1,c2,...,cn. Определитель этой системы - определитель Вронского W(x).
При эта система имеет нетривиальное решение c1,c2,...,cn, следовательно, в каждой точке её определитель равен нулю. Итак, W(x) = 0 при , т.е.W(x)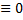 
на (a, b).
Теорема Пусть y1(x), y2(x), …, yn(x) - частные решения линейного однородного дифференциального уравнения. Если определитель Вронского этой системы функций равен нулю в некоторой точке 
, то система функций y1(x), y2(x), …, yn(x) линейно зависима, и её определитель Вронского тождественно равен нулю на (a, b).
Док-во:
Пусть 
. Тогда однородная система линейных алгебраических уравнений, для которой W(
) является определителем,
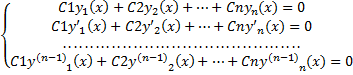
имеет нетривиальное решение относительно C1, C2, …, Cn. Рассмотрим линейную комбинацию функций y1(x), y2(x), …, yn(x) с этими коэффициентами C1, C2, …, Cn:
y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x).
Эта функция удовлетворяет уравнению 
и, как следует из приведённой выше системы, имеет нулевые начальные условия в точке x0, т.е. является решением задачи Коши
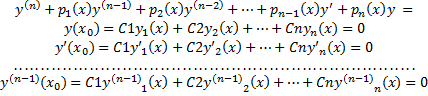
Этой же задаче Коши удовлетворяет и функция y(x) = 0, тождественно равная нулю на интервале (a, b). Вследствие единственности решения задачи Коши y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x) = 0 для . Таким образом, система функций y1(x), y2(x), …, yn(x) линейно зависима на (a, b), и по Теореме о вронскиане линейно зависимой системы её определитель Вронского тождественно равен нулю на (a, b).
|
|
|
Теорема. Если определитель Вронского W(x) системы y1(x), y2(x), …, yn(x) частных решений линейного однородного дифференциального уравнения отличен от нуля в некоторой точке , то W(x) отличен от нуля в любой точке этого интервала.
Док-во легко проводится от противного. Если предположить, что в некоторой точке 
определитель Вронского равен нулю, то по предыдущей теореме он тождественно равен нулю на (a, b), что противоречит условию 
.
Содержание двух предыдущих теорем можно изложить так:
Теорема. Если W(x) - определитель Вронского системы y1(x), y2(x), …, yn(x) частных решений линейного однородного дифференциального уравнения, то либо 
на интервале (a, b) (что означает линейную зависимость этих решений на (a, b)), либо в любой точке этого интервала (что означает линейную независимость этих решений на (a, b)).
Существование фундаментальной системы решений линейного однородного уравнения.
Теорема о существовании фундаментальной системы решений линейного однородного дифференциального уравнения.
Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.
Док-во. Возьмём любой числовой определитель n -го порядка, не равный нулю
Возьмём любую точку и сформулируем для уравнения 
n задач Коши, причём начальные условия в точке x0 для i-ой задачи возьмём из i-го столбца этого определителя:
Пусть y1(x), y2(x), …, yn(x) - решения этих задач. Эта система линейно независима на (a, b), так как её определитель Вронского в точке x0 равен взятому числовому определителю и отличен от нуля, следовательно, это фундаментальная система решений. Теорема доказана.
|
|
|
|
|
|
