 |
Второй закон термодинамики
|
|
|
|
Второй закон термодинамики позволяет определить возможность протекания и направление процесса в изолированных системах при данных условиях.
Для изолированных систем критерием, который характеризует возможность, направление и предел самопроизвольного протекания термодинамических процессов, служит особая функция состояния – энтропия S. Энтропия является мерой вероятности состояния системы. Она возрастает при переходе вещества из более упорядоченного состояния в менее упорядоченное, например при переходе вещества из кристаллического состояния в жидкое и из жидкого в газообразное, при растворении кристаллов, при расширении газов. Все процессы, в результате которых упорядоченность системы возрастает, сопровождаются уменьшением энтропии.
Согласно второму закону термодинамики в изолированных системах могут совершаться только такие процессы, при которых энтропия системы возрастает, и подобный самопроизвольный процесс может идти только до такого состояния, при котором энтропия обладает максимальным значением (для данных условий).
Изменение энтропии при обратимом превращении и постоянной температуре может быть выражено уравнением
 . (1.11)
. (1.11)
Обратимым превращением является бесконечно медленный переход системы из одного равновесного состояния в другое через непрерывный ряд равновесных состояний. При обратимом протекании процесса система все время находится в состоянии термодинамического равновесия, когда значения ее параметров в каждый момент одинаковы в любой точке и не меняются во времени. Для необратимых процессов

 . (1.12)
. (1.12)
Самопроизвольно протекающие процессы необратимы, т.е. систему нельзя вернуть в исходное состояние, не производя каких-либо изменений в ней самой или в окружающей среде. Поскольку энтропия – функция состояния, ее изменение не зависит от того, как протекает процесс: обратимо или необратимо. Из (1.11) и (1.12) следует, что  .
.
|
|
|
В изолированной системе  и
и  . Из этого следует, что в изолированной системе при обратимом протекании процесса
. Из этого следует, что в изолированной системе при обратимом протекании процесса  ,а при необратимом
,а при необратимом  . Процессы с уменьшением энтропии, когда
. Процессы с уменьшением энтропии, когда  ,в такой системе невозможны. Таким образом, энтропия является критерием направленности протекания процессов для изолированной системы. Процесс протекает самопроизвольно, если
,в такой системе невозможны. Таким образом, энтропия является критерием направленности протекания процессов для изолированной системы. Процесс протекает самопроизвольно, если  , а при
, а при  ,система находится в состоянии термодинамического равновесия.
,система находится в состоянии термодинамического равновесия.
Изменение энтропии в химических процессах вычисляется так же, как и изменение любой функции состояния:
 (1.13)
(1.13)
В отличие от энтальпии образования энтропия простого вещества не равна нулю.
На практике чаще всего имеют дело с закрытыми системами, которые обмениваются с внешней средой энергией, но не обмениваются веществом. Для такой реальной системы, находящейся при постоянной температуре и давлении, критерием направленности процесса является функция состояния, называемая изобарно-изотермическим потенциалом, или энергией Гиббса, и определяемая по уравнению
∆G = ∆H - T∆S. (1.14)
Для изобарно-изотермических процессов условием равновесия будет
∆G = 0. Условием самопроизвольного протекания процесса − ∆G < 0.
При ∆G > 0 реагенты не могут превращаться в продукты, а принципиально возможна обратная реакция – превращение продуктов в реагенты. Стандартный изобарно-изотермический потенциал образования соединения  равен изменению изобарного потенциала при реакциях образования этого соединения из простых веществ в стандартных условиях (р = 1013 ГПа, Т = 298 К). Величину
равен изменению изобарного потенциала при реакциях образования этого соединения из простых веществ в стандартных условиях (р = 1013 ГПа, Т = 298 К). Величину  можно вычислить из табличных значений
можно вычислить из табличных значений  и
и  участников реакции. Свободную энергию Гиббса химической реакции, которая определяет возможность протекания любого химического превращения в стандартных условиях, можно рассчитать по уравнению
участников реакции. Свободную энергию Гиббса химической реакции, которая определяет возможность протекания любого химического превращения в стандартных условиях, можно рассчитать по уравнению
|
|
|
 . (1.15)
. (1.15)
Вопросы и задачи к главе 1
1. Что такое термодинамическая система? Какие вы знаете типы систем?
2. В чем сущность первого закона термодинамики?
3. Чему равен тепловой эффект изобарного и изохорного процессов?
4. Как формулируется закон Гесса и какие следствия из него вытекают?
5. Что такое функции состояния?
6. Что называется стандартной теплотой образования и сгорания?
7. В чем сущность второго закона термодинамики?
8. Что такое термодинамически обратимые и необратимые процессы?
9. Каков физический смысл энтропии?
10. Что такое изобарно-изотермический потенциал и как его можно вычислить?
11. Пользуясь теплотами образования, рассчитайте тепловой эффект следующих реакций в стандартных условиях:
CO(r) + H2O(r) = CO2(r) + H2(r);
Fl2O3(k) + 2Al(k) = Al2O3(k) + 2Fl(k).
 (кДж/моль);
(кДж/моль);
CO(r) - 110,6
H2O(r) - 241,98
CO2(r) - 393,8
Fl2O3(k) - 822,7
Al2O3(k) - 1676,8
Ответ: - 41,2 кДж, - 854,1 кДж.
Рассчитайте  следующей реакции:
следующей реакции:
3H2(r) + N2(r) = 2NH3(r)
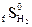 = 130,7 Дж/моль град
= 130,7 Дж/моль град
 = 199,9 Дж/моль град
= 199,9 Дж/моль град
 = 238,36 Дж/моль град
= 238,36 Дж/моль град
Ответ: - 206,8 кДж/моль град
Рассчитайте изменение энтальпии, энтропии и энергии Гиббса для реакции окисления NO в NO2 в стандартных условиях;
2NO + О2 = 2NO2
 , кДж/ моль
, кДж/ моль  , кДж/ моль∙К
, кДж/ моль∙К
NO 90,31 NO 210,7
NO2 33,00 NO2 240,2
O2 0 O2 205,0
Ответ:  = - 56,8 кДж/ моль;
= - 56,8 кДж/ моль;  = - 72,9 кДж/ моль;
= - 72,9 кДж/ моль;
 = - 29,0 кДж/ моль.
= - 29,0 кДж/ моль.
|
|
|


