 |
Аналоговый пилообразный фазовый сигнал
|
|
|
|
Или геродинная модуляция
Проблема стабильности акусто-оптического сдвига частоты теперь полностью преодолена с помощью пилообразного сигнала фазы [8–11]. Частота является производной фазы и пилообразная модуляция 
(где 
– наклон), которая применяется в фазовом модуляторе вместо сдвига частоты, эквивалентно сдвигу частоты 
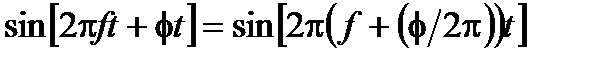. (8.6)
Такая обработка схемы, также называемая геродинная модуляция, позволяет работать положительно или отрицательно около нуля, в зависимости от знака пилообразного сигнала фазы, тем самым исключая предшествующую потребность в высоком центре частоты, который показал обнуление внутренней обратимости кольцевого интерферометра. Однако пилообразный сигнал не может быть бесконечным, и на практике пилообразной модуляции форма используется с очень быстрым возвратом на сброс (Рисунок 8.3). Это требует фазового модулятора с преобладанием эффективности над большой пропускной способностью, которая является одним из главных технических преимуществ интегральной оптики (см. приложение 3).
Рисунок 8.3. Аналоговый пилообразной сигнал модуляции фазы 
и индуцированная обратной связью разность фаз 
|
| (Наклон) |
Влияние на гироскоп можно просмотреть, непосредственно наблюдая групповую задержку разницы 
между длинным и коротким путями, связывающими фазовый модулятор и разделитель. Как в случае модуляции смещения (см. раздел 3.2.2), один пилообразный сигнал фазовой модуляции 
применяется для двух противоположных волн; но, в связи с задержкой это создает обратную разность фаз 
с
(8.7)
Это равно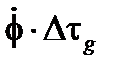 
в ходе пилообразного сигнала и 
во время после сброса. Значение 
определяет высоту переустановки фазы. Эта переустановка побуждает ошибку, если не равно 2π рад (или кратно 2 π), периодического отклика интерферометра [9,10].
|
|
|
Предполагая, что при закрытой петле наклон 
отрегулирован компенсацией индуцируемой вращением разности фаз 
и что общая разность фаз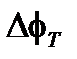 
обнулена:
(8.8)
то есть:
(8.9)
После сброса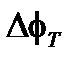 
становится равной вместо нуля. Предполагая для простоты, что откликом интерферометра является смещение синуса (Рисунок 8.4), сигнал будет нулевым, когда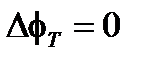 
, но становится 
в течение времени после каждого сброса. Пропускание этого ложного сигнала было предложено в [8], но это показало, что на самом деле очень удобно сигнал ошибки для проверки эффективности фазового модулятора со второй обратной петлей активировать при каждой перезагрузке [9].
С такой второй обработкой петли сброс точно контролируется на 2π рад, и поэтому подсчет положительных и отрицательных установок обеспечивает точное измерение угла поворота.Наклон пропорционален скорости Ω, поскольку 
:
(8.10)
| Рисунок 8.4. Эффект установки фазового наклона |
| Сигнал ошибки |
| Отклик |
, имеем
(8.11)
Каждый сброс соответствует точно 2π рад, а также угловому приращению 
, определяемому как
(8.12)
где Т – период пилообразной модуляции, и поскольку 
для любого налона, имеем
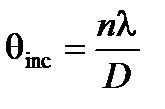(8.13)
Это добавочное значение не зависит от длины катушки L, но обратно пропорционально диаметру катушки D. Для длины волны λ = 850 нм продукт 
равен 25 arcsec·см. Заметим, что частота этих "2π-приращений" такая же, как полученная при прямом смещении частоты с обратной связью и как естественно генерированной в лазерном гироскопе (см. раздел 2.2.1).
Важной особенностью этой техники обработки пилообразного сигнала является, что контроль 2π установки не нужно осуществлять очень точно, поскольку он имеет только третий порядок зависимости от фактического масштаба фактора точности [10]. Как видно из (Рисунок 8.5), начиная с идеального наклона фазы, есть небольшое снижение 
в росте амплитудной модуляции цепи, фактическая модуляция 
связана с идеальной модуляцией 
соотношением
|
|
|
(8.14)
и индуцирует разность при
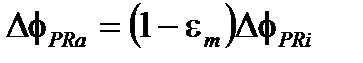(8.15)
Пилообразный фазовый сигнал теперь недостаточен для компенсации индуцируемой вращением разности фаз 
и общая разность фаз становится
(8.16)
Тем не менее, если уменьшить наклон пилообразного сигнала, высота сброса также уменьшится с тем же коэффициентом 
и в течение времени 
после сброса, актуальная чрезмерная компенсация фазы 
:
| Рисунок 8.5. Эффект превращения идеального усиления в цепи модуляции |
| Линейный участок |
| Верхняя компенсация |
| Нижняя компенсация |
(8.17)
Таким образом, за полный период T пилообразной модуляции и при условии, что отклик смещенного синуса в открытой петле сигнал ошибки, этот сигнал
(8.18)
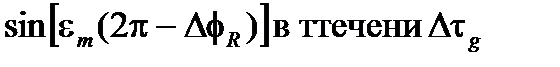
Если эти фазовые ошибки небольшие, отклик синуса ответ может быть линейным (игнорируя члены третьего порядка) и получаем средний сигнал
(8.19)
но поскольку
(8.20)
(8.21)
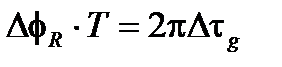(8.22)
средний сигнал ошибки 
остается равным нулю независимо от точного значения сброса, если 
является достаточно небольшой, чтобы держать оперативные точки в линейной части отклика синуса.
Эта схема обратной связи аналогового пилообразного фазового сигнала выглядит очень привлекательной, но она требует очень короткого и стабильного времени возврата для того, чтобы давать высокую стабильность и линейность [10,12]. Как правило, стабильность 10 млн–1 требует времени возврата менее, чем 1% от транзитного времени через катушку (т.е. меньше, чем несколько десятков наносекунд).
|
|
|
