 |
Интерферометра с широкополосным источником
|
|
|
|
Предполагая, что можно добиться идеальных измерений с одной только разностью фаз Саньяка 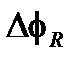 с обнулением фазы в схеме замкнутой петли, коэффициент масштабирования остается, как мы уже видели, связанным с эквивалентной площадью катушки и длиной волны источника. Площадь катушки дает типичные изменения менее, чем млн–1 от Кельвина при тепловом расширения кремния, которое требует некоторого контроля и моделирования для высокоточных приложений. Стабильность длины волны решить сложнее. Например источники из полупроводниковых диодов, которые являются популярными источниками для И-ВОГ, имеют типичную длину волны, изменяющуюся с температурой около 400 млн–1 за Кельвин и около 40 млн–1 за милиампер с прохождением тока, даже без учета таких дополнительных факторов, как дисперсионное твердение или эффекта обратной связи при возвращении света к источнику. Контроль температуры источника и стабилизация сигнала достаточны для средней точности в диапазоне 100 млн–1, но высокопроизводительные приложения требуют прямого управления длиной волны, чтобы достигать диапазона млн–1.
с обнулением фазы в схеме замкнутой петли, коэффициент масштабирования остается, как мы уже видели, связанным с эквивалентной площадью катушки и длиной волны источника. Площадь катушки дает типичные изменения менее, чем млн–1 от Кельвина при тепловом расширения кремния, которое требует некоторого контроля и моделирования для высокоточных приложений. Стабильность длины волны решить сложнее. Например источники из полупроводниковых диодов, которые являются популярными источниками для И-ВОГ, имеют типичную длину волны, изменяющуюся с температурой около 400 млн–1 за Кельвин и около 40 млн–1 за милиампер с прохождением тока, даже без учета таких дополнительных факторов, как дисперсионное твердение или эффекта обратной связи при возвращении света к источнику. Контроль температуры источника и стабилизация сигнала достаточны для средней точности в диапазоне 100 млн–1, но высокопроизводительные приложения требуют прямого управления длиной волны, чтобы достигать диапазона млн–1.
Первый фундаментальный вопрос заключается в точном определении эффективной длины волны, включающей в себя коэффициент масштабирования, при котором широкополосный источник, необходимый для высокой производительности, имеет относительную спектральную ширину в несколько процентов, которая на несколько порядков больше наблюдаемой стабильности млн–1. Как объясняется в разделе 2.3.1, вращение, вызывающее разность фаз 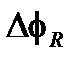 , может быть выражено эквивалентной разностью хода
, может быть выражено эквивалентной разностью хода  , которая прекрасно зависит от длины волны:
, которая прекрасно зависит от длины волны:
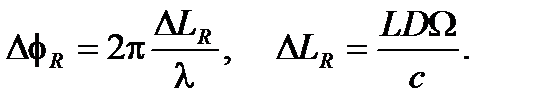 (8.30)
(8.30)
Ответ внутренней несмещенной интерференции
|
|
|
 (8.31)
(8.31)
где γ c – функция когерентности источника, измеряется сканированием в вакууме интерферометром, подобным интерферометру Майкельсона, и где λcent – центральная длина волны в спектре. Тем не менее, этот простой результат применяется только в том случае, если спектр симметричен по отношению к оптической пространственной частоте (т.е. обратной длине волны λ) с центральной частотой, относящейся к максимальной мощности. На практике спектр источника гироскопа имеет значительную асимметрию и, как описано в приложении 1, ответ несмещенной интерференции в самом общем случае
 (8.32)
(8.32)
где γ cе – это функция когерентности даже компонент асимметричного спектра, и λ – средняя длина волны. По сравнению с простым симметричным случаем имеется дополнительный член  , который учитывает нечетные компоненты спектра. Когда гироскоп эксплуатируется на центральной полосе, как это обычно бывает, этот дополнительный член является на практике незначительным, тем не менее, если он эксплуатируется в широком динамическом диапазон, переход от фактической средней длины волны дает возрастающую разность фаз, поскольку при пересечении нуля ответ переменного члена интерферометра не является больше точно периодическим.
, который учитывает нечетные компоненты спектра. Когда гироскоп эксплуатируется на центральной полосе, как это обычно бывает, этот дополнительный член является на практике незначительным, тем не менее, если он эксплуатируется в широком динамическом диапазон, переход от фактической средней длины волны дает возрастающую разность фаз, поскольку при пересечении нуля ответ переменного члена интерферометра не является больше точно периодическим.
Это видно непосредственно в отношении интерферометра как фильтра с передачей  в зависимости от длины волны λ (или пространственной частоты σ) для заданной разности хода
в зависимости от длины волны λ (или пространственной частоты σ) для заданной разности хода 
 (8.33)
(8.33)
Широкий спектр мощности  дает интегральный отклик,
дает интегральный отклик,
 (8.34)
(8.34)
Для нулевых точек пересечения переменная часть ответа косинуса, средняя частота 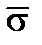 является такой, что функция
является такой, что функция 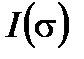 с
с  имеет нулевой интеграл (Рисунок 8.16). Если спектр симметричен (с точки зрения частоты), проблема проста и среднее значение центральное значение; но когда он асимметричный, проблема является более сложной и зависит от порядка
имеет нулевой интеграл (Рисунок 8.16). Если спектр симметричен (с точки зрения частоты), проблема проста и среднее значение центральное значение; но когда он асимметричный, проблема является более сложной и зависит от порядка
|
|
|
| Передача |
| Спектр |
Рисунок 8.16. Интерферометрическое определение средней пространственной частоты 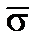 по ширине спектра по ширине спектра
|
| Среднее |
полосы. В частности, среднее значение 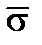 не равно значению
не равно значению  , которое соответствует максимальной интенсивности. Линейное среднее, определенное спектром с линейной функцией вместо синуса (Рисунок 8.17) является
, которое соответствует максимальной интенсивности. Линейное среднее, определенное спектром с линейной функцией вместо синуса (Рисунок 8.17) является
| Рисунок 8.17. Определение линейного среднего значения асимметричного по ширине спектра |

| Составляющая сигнала |
| Спектр |
| Линейное среднее значение |
| Линейная функция |
хорошим приближением для работы гироскопа вокруг нуля порядка  рад [17]. Это линейное усреднение фактически эквивалентно центру тяжести.
рад [17]. Это линейное усреднение фактически эквивалентно центру тяжести.
Эффект модуляции фазы
До сих пор, мы рассмотрели несмещенный отклик интерферометра; однако, как мы уже видели, И-ВОГ должна оперировать смещением модулированной фазы и обнулением фазы обратной связи. Таким образом, длину волны, зависящую от модуляторов, также придется учитывать.
В случае открытой петли демодулированный смещенной отклик на заданной длине волны является всегда синусом независимо от глубины модуляции, поэтому даже с длиной волны, зависящей от фазы модулятора, общий отклик с широким спектром также совершенный синус. Амплитуда этого отклика открытой петли слегка зависит от спектра, но на практике гораздо более важны другие источники ошибок коэффициента масштабирования.
Со схемой обнуления фазы, использующей модуляторы Брэгга (см. раздел 8.2.1), существует обратная связь смещения частоты  , которая зависит от длины волны, поэтому коэффициент масштабирования этого спектра зависит, как в несмещенном случае. С аналоговыми или цифровыми ступенчатыми сигналами (см. разделы 8.2.2 и 8.2.3) проблема несколько более деликатна. Фазовый модулятор на основе упруго-оптического эффекта такой, как пьезоэлектрические модулятор, или модулятор на основе электрооптического эффекта Поккельса в интегральной оптике, является на самом деле "модулятором разности хода». Учет дрейфа напряжения Vd дает разность хода, которая в первом приближении не зависит от длины волны. Модуляция проявляется главным образом в изменении геометрической длины или изменении показателя преломления, которые почти не зависят от длины волны. Это дает для заданного ступенчатого или шагового напряжения разность фаз обратной связи
, которая зависит от длины волны, поэтому коэффициент масштабирования этого спектра зависит, как в несмещенном случае. С аналоговыми или цифровыми ступенчатыми сигналами (см. разделы 8.2.2 и 8.2.3) проблема несколько более деликатна. Фазовый модулятор на основе упруго-оптического эффекта такой, как пьезоэлектрические модулятор, или модулятор на основе электрооптического эффекта Поккельса в интегральной оптике, является на самом деле "модулятором разности хода». Учет дрейфа напряжения Vd дает разность хода, которая в первом приближении не зависит от длины волны. Модуляция проявляется главным образом в изменении геометрической длины или изменении показателя преломления, которые почти не зависят от длины волны. Это дает для заданного ступенчатого или шагового напряжения разность фаз обратной связи  , обратно пропорциональную длине воны:
, обратно пропорциональную длине воны:
|
|
|
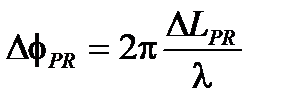 (8.35)
(8.35)
где  – эквивалентная разность хода, вызванная ступенчатым сигналом. Поэтому вращение дает
– эквивалентная разность хода, вызванная ступенчатым сигналом. Поэтому вращение дает
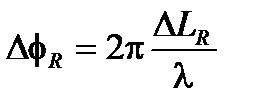 (8.36)
(8.36)
Обе разности фаз  и
и  имеют ту же самую зависимость от длины волны, и ступенчатый фазовый сигнал обратной связи должнн быть глобально независимым от длины волны: для любой длины волны, задаваемой напряжением, получаем ту же разность хода
имеют ту же самую зависимость от длины волны, и ступенчатый фазовый сигнал обратной связи должнн быть глобально независимым от длины волны: для любой длины волны, задаваемой напряжением, получаем ту же разность хода  , которая компенсирует разность
, которая компенсирует разность  , вызванную вращением. Однако это было бы верно, только если эффект сброса выходит наружу. В этом случае другие причины дрейфа модулятора эффективны или усиливают движение электроники (температура, в частности) а затем станут доминирующими. Мы видели (раздел 8.2.2) что небольшое изменение коэффициента усиления фазовой модуляции цепи имеет эффект только третьего порядка точности на коэффициент масштабирования при сбросе на 2π, и когда сигнал после сброса принимается во внимание. Изменения длины волны эквивалентно изменению разности фаз, так как
, вызванную вращением. Однако это было бы верно, только если эффект сброса выходит наружу. В этом случае другие причины дрейфа модулятора эффективны или усиливают движение электроники (температура, в частности) а затем станут доминирующими. Мы видели (раздел 8.2.2) что небольшое изменение коэффициента усиления фазовой модуляции цепи имеет эффект только третьего порядка точности на коэффициент масштабирования при сбросе на 2π, и когда сигнал после сброса принимается во внимание. Изменения длины волны эквивалентно изменению разности фаз, так как  . Таким образом, изменение длины волны не изменяет влияние среднего ступенчатого сигнала обратной связи, в то время как оно изменяет вызванную вращением разность фаз первого порядка
. Таким образом, изменение длины волны не изменяет влияние среднего ступенчатого сигнала обратной связи, в то время как оно изменяет вызванную вращением разность фаз первого порядка  . Затем основная длина волны, зависящая от эффекта Саньяка, извлекается с обратной связью ступенчатого сигнала, когда эффект сброса не выходит наружу. Несмотря на этот недостаток, контролируемый 2π сброс является предпочтительным, поскольку длина волны, может регулироваться независимо друг от друга, в то время как эффективный дрейф других источников модуляции не будет обнаружен.
. Затем основная длина волны, зависящая от эффекта Саньяка, извлекается с обратной связью ступенчатого сигнала, когда эффект сброса не выходит наружу. Несмотря на этот недостаток, контролируемый 2π сброс является предпочтительным, поскольку длина волны, может регулироваться независимо друг от друга, в то время как эффективный дрейф других источников модуляции не будет обнаружен.
|
|
|


